
第一章函数与极限 高等数学少学时 二、函数的几种特性 1.函数的有界性 设函数f(x)的定义域为D,数集XCD如果存在正数M, 对于任一x∈X,不等式 Lf(x)≤M 都成立,则称f(x)在X上有界.如果这样的M不存在,就称f(x) 在X上无界. 例如,函数f(x)=sinr在(-o,+o)内,恒有sinx≤1, 故fx)在(-o0,+0)内有界. 函数fx)=x在(仁o,+oo)内,对于任意的常数M>0, 只要|x|>M,则有f(x)川>M,所以f(x)在(-oo,+o)内无界. 北京邮电大学出版社 11
11 二、函数的几种特性 1.函数的有界性 设函数 f (x)的定义域为D,数集 X D. 如果存在正数M, 对于任一 x ∈X,不等式 f (x) M 都成立,则称 f (x)在X上有界.如果这样的M不存在,就称 f (x) 在X上无界. 例如,函数 f (x) = sinx 在(-∞,+∞)内,恒有 sin x 1, 故 f (x)在(-∞,+∞)内有界. 函数 f (x)=| x |在(-∞,+∞)内,对于任意的常数M > 0, 只要| x | > M,则有| f (x) | > M,所以 f (x)在(-∞,+∞)内无界
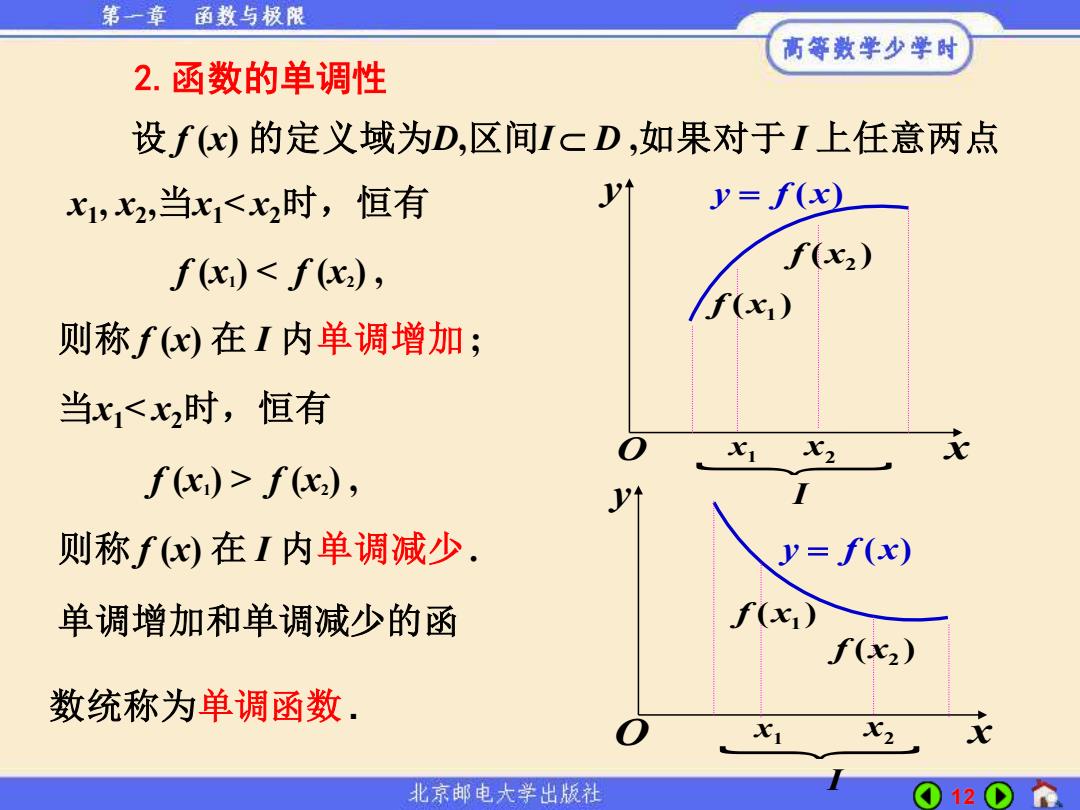
第一章函数与极限 高等数学少学时 2.函数的单调性 设f(x)的定义域为D,区间IcD,如果对于I上任意两点 飞1,2,当x1<2时,恒有 y=f(x) f(x)<f(x), f(x2) If(x) 则称f(x)在I内单调增加; 当x1<x2时,恒有 X2 x f(x)>f(x), 则称f(x)在I内单调减少. y=f(x) 单调增加和单调减少的函 f(x) f(x2) 数统称为单调函数. 2,x 北京邮电大学出版社 12
12 2.函数的单调性 设 f (x) 的定义域为D,区间I D ,如果对于 I 上任意两点 f (x1) < f (x2) , 则称 f (x) 在 I 内单调增加; 则称 f (x) 在 I 内单调减少. f (x1) > f (x2) , x1 , x2 ,当x1< x2时,恒有 当x1< x2时,恒有 单调增加和单调减少的函 数统称为单调函数 . ( ) x1 f ( ) x2 f x1 x2 y = f (x) x y O I y = f (x) ( ) x1 f ( ) x2 f I x y O x1 x2