
积分中值定理 设函数f∈C[a,b],g∈[a,b],g在a,b]上不改变符号, 则归5∈[a,b],使fx)8(xd=f(5)fg(xd 证明:m=mmf,M=m8x,则m≤f(≤M,x∈[a,小如果g≥0, 则nmg()≤fx)g(x)≤Mg(x),故mg(x)dk≤∫fx)gx)d≤Mg()d 若8达>&上式两边同除gNi有m气g ≤M,由连续 ∫gxd 函数介值性质,至少存在一点5e2.bf付=fx8(md ['sd 若0gx)=0:命题显然
积分中值定理 [ , ] [ , ] [ , ] [ , ], ( ) ( ) ( ) ( ) b b a a f C a b g a b g a b a b f x g x dx f g x dx 设函数 , , 在 上不改 , 则 号 使 R 变符 [ , ] [ , ] min ( ) , max ( ) , ( ) , , 0, ( ) ( ) ( ) ( ), ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 ( ) , ( ) , , x a b x a b b b b a a a b b b a b a a a m f x M f x m f x M x a b g mg x f x g x Mg x m g x dx f x g x dx M g x dx f x g x dx g x dx g x dx m M g x dx a b f 证明: 则 ,如果 则 故 若 :上式两边同除 ,得 由连续 函数介值性质,至少存在一点 ( ) ( ) , ( ) ( ) 0 : b a b a b a f x g x dx g x dx g x dx 若 命题显然
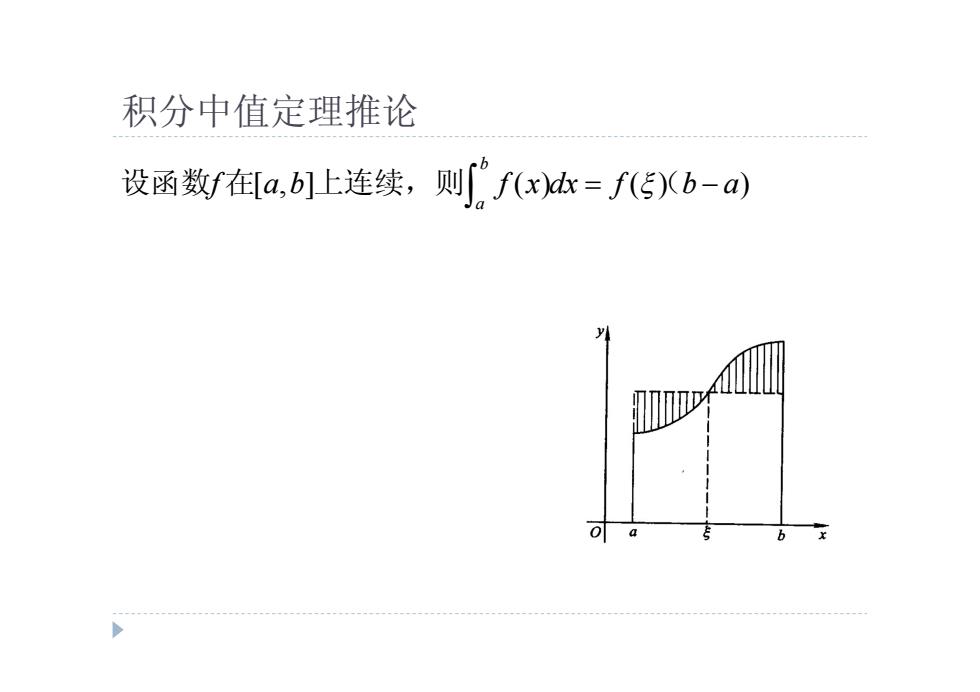
积分中值定理推论 设函数f在[a,b]上连续,则f(x)k=f(5)(b-a)
积分中值定理推论 [ , ] ( ) ( ) ) b a f a b f x dx f b a 设函数 在 上连续,则 (

例 设fe[a,b],且1-∫心fx)dk>0,则有子区间c,d]c[a,b1和u>0, 使在区间[c,d]上成立f(x)≥4 证明:f∈[a,b],则存a,b的一个分划P={x,x,,x}使得对 从属于P的年何介点集三,成立空/(传)>号0,记m=则 立m>分0显然在和式中至少有一项大于零,设这一项为第项, 取μ=m[c,d]=[x-,x]
例 [ , ], ( ) 0, [ , ] [ , ] 0, [ , ] ( b a f a b I f x dx c d a b c d f x 设 且 则有子区间 和 使在区间 上成立 ) R 1 0 1 , 1 1 , 1 [ , ], [ , ] , , , , 0, inf ( ) 2 0, 2 [ , ] , i i n n i i i x x x i n i i i k k k f a b a b P x x x I P f x m f x I m x k m c d x x 证明: R 则存在 的一个分划 ,使得对 从属于 的任何介点集 成立 记 ,则 显然在和式中至少有一项大于零,设这一项为第 项, 取

例 设非负函数f∈[a,b],且有子区间[c,d]c[a,b],使得在[c,d]上, fx)>0,则有∫fx)d>0 正明:不妨设fah-0记[a,6,]-a,61则ve, ]ab=ab-小neN.Yxe[o]0<fx 则归5e[a,610<f传)水→0矛盾
例 [ , ], [ , ] [ , ] [ , ] ( ) 0, ( ) 0 b a f a b c d a b c d f x f x dx 设非负函数 R 且有子区间 ,使得在 上, 则有 0 0 1 1 1 ( ) =0, , [ , ] , 1 , , , , , , , ,0 ( ) 1 , 0 0, b n a n n n n n n n n f x dx a b a b n a b a b a b n x a b f x n a b f n 证明:不妨设 记 ,则 则 , 矛盾

例 证明。 in"xdx=0 证.0≤sn≤sn迹+sin迹 s分m →0
例 / 2 0 lim sin 0 n n xdx 证明: / 2 / 2 / 2 0 0 / 2 0 sin sin sin sin 0 2 2 2 n n n n xdx xdx xdx 证: