
电路习题集第十三章重一阶电路一阶电路第十三章一、本章要求1.掌握换路、时间常数、自由分量与强迫分量、稳态响应玉暂态响应概念。2.,会建立一阶电路的微分方程:计算一阶电路的零输入响应、零状态响应与全响应。求解单位冲激响应和单位阶跃响应。二内容提要1:在动态电路中,从一个(稳定)状态变化到另一个(稳定)状态,需要一个过渡过程也称动态(暂态、瞬态)过程。2.换路定则:u(0_)=u(0),i(0_)=i(0)(13-1)3.一阶电路的零输入响应是电路在输入为零(无外加激励)时,由非零初始状态引起的(13-3)响应。其中:u。=u.(O)e,t=RC(时间常数)Ti =i(0+)e,=%(时间常数)(13-4)/R4.一阶电路的零状态响应是电路在零初始状态,由输入(外加激励)产生的响应。其中:Iu。=U,(1-e),t=RC(时间常数)(13-5)1i =l,(-e),t=/(时间常数)(13-6)TR5.一阶电路的全响应是电路的输入(外加激励)和初始状态都不为零时的响应。全响应=零输入响应+零状态响应=暂态分量+稳态分量(13-7)三要素法:f(t)= f(o0)+[f(O.)- f(c0)le r其中:f(O.)为换路后的初始条件,f(co)为换路后的稳态值,T是时间常数。6.零状态电路对单位阶跃函数ε(t)的响应s(t)称作单位阶跃响应,对单位冲击函数(t)ds(t)的响应h(t)称作单位冲击响应。h(t)=(13-8)dt三例题例13-1已知如图所示电路(13-1(a)图),s打开前电路已经稳定,求换路后的i(t)。(电阻的单位为欧姆,电容的是微法)解:(1)0_等校电路如图13-1(b),105
电路习题集 第十三章 一阶电路 105 第十三章 一阶电路 一、本章要求 1. 掌握换路、时间常数、自由分量与强迫分量、稳态响应玉暂态响应概念。 2. 会建立一阶电路的微分方程;计算一阶电路的零输入响应、零状态响应与全响应。求 解单位冲激响应和单位阶跃响应。 二 内容提要 1. 在动态电路中,从一个(稳定)状态变化到另一个(稳定)状态,需要一个过渡过程 也称动态(暂态、瞬态)过程。 2. 换路定则: (0 ) (0 ) uc − = uc + , (0 ) (0 ) L − = L + i i (13-1) 3.一阶电路的零输入响应是电路在输入为零(无外加激励)时,由非零初始状态引起的 响应。其中: u u e RC t c = c = − + (0 ) , (时间常数) (13-3) R i i e L t L = L = − + (0 ) , (时间常数) (13-4) 4.一阶电路的零状态响应是电路在零初始状态,由输入(外加激励)产生的响应。其中: u U e RC t c = s − = − (1 ), (时间常数) (13-5) R i I e L t L = s − = − (1 ), (时间常数) (13-6) 5.一阶电路的全响应是电路的输入(外加激励)和初始状态都不为零时的响应。 全响应=零输入响应+零状态响应=暂态分量+稳态分量 三要素法: t f t f f f e − ( ) = () +[ (0+ ) − ()] (13-7) 其中: (0 ) + f 为换路后的初始条件, f () 为换路后的稳态值, 是时间常数。 6. 零状态电路对单位阶跃函数 (t) 的响应 s(t)称作单位阶跃响应,对单位冲击函数 (t) 的响应 h(t)称作单位冲击响应。 dt ds t h t ( ) ( ) = (13-8) 三 例题 例 13-1 已知如图所示电路(13-1(a)图),s 打开前电路已经稳定,求换路后的 i(t)。(电 阻的单位为欧姆,电容的是微法) 解:(1) − 0 等校电路如图 13-1(b)
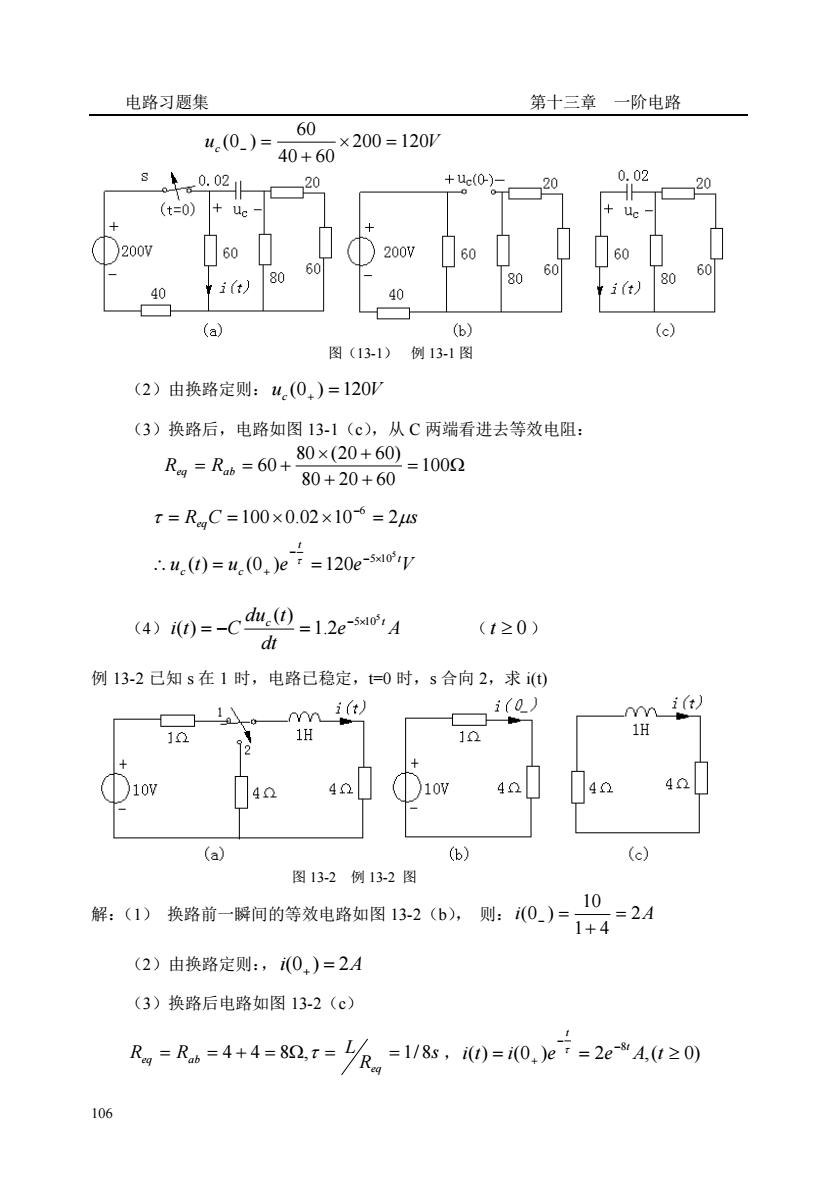
电路习题集第十三章一阶电路60x200=120Vu.(0_)40 + 600. 02+uc(0-)_0.02202020(t=0)u.c60200V200V6060606060808080i(t)i (t)4040(b)(a)(c)图(13-1)例13-1图(2)由换路定则:u.(0.)=120V(3)换路后,电路如图13-1(c),从C两端看进去等效电阻:80×(20+60)Reg = Rab = 60+3=100280+20+60T=RC=100×0.02×10-6=2μs.. u.(0)= u.(0+)e* =120e-5xl0rV(4) ()=-cdm,@ =1.2e-si0: A(t≥0)dt例13-2已知s在1时,电路已稳定,t=0时,s合向2,求i(t)i(t)i(α)it)1V1H121H1010404010V404010V402(a)(b)(c)图13-2例13-2图102A则:(0_)解:(1)换路前一瞬间的等效电路如图13-2(b),1+ 4(2)由换路定则:,(0.)=2A(3)换路后电路如图13-2(c)=1/8s , i(t)= i(0+)e = 2e-8 A,(t≥0)Re. = Rab =4+4=82,t=106
电路习题集 第十三章 一阶电路 106 uc 200 120V 40 60 60 (0 ) = + − = 图(13-1) 例 13-1 图 (2)由换路定则: uc (0+ ) =120V (3)换路后,电路如图 13-1(c),从 C 两端看进去等效电阻: = + + + = = + 100 80 20 60 80 (20 60) Req Rab 60 u t u e e V R C s t t c c eq 5 5 10 6 ( ) (0 ) 120 100 0.02 10 2 − − + − = = = = = (4) e A dt du t i t C c t 5 5 10 1.2 ( ) ( ) − = − = ( t 0 ) 例 13-2 已知 s 在 1 时,电路已稳定,t=0 时,s 合向 2,求 i(t) 图 13-2 例 13-2 图 解:(1) 换路前一瞬间的等效电路如图 13-2(b), 则: i 2A 1 4 10 (0 ) = + − = (2)由换路定则:, i(0+ ) = 2A (3)换路后电路如图 13-2(c) s R R R L eq eq = ab = 4 + 4 = 8, = = 1/ 8 , ( ) (0 ) 2 ,( 0) 8 = = − − + i t i e e A t t t

电路习题集第十三章一阶电路例13-3在t=0时,图13-3(a)中s打开,求uc。ReqRRR1PRUcUocRUcRUDuoceo(d)(a)(b)(c)图13-3例13-3图解:(1)u(0_)=u(0)=0v(2)换路后,从C两端求戴维南等校电路,将电路化简成RC模型电路,如图13-3(d)分别由图13-3(b)、(c)可以求得:u=RI,R=2R(3) T= Re.C=2RC,..u.(t)=uoc(1-e)= RI,(1-e 2RC),(t≥0)例13-4图中,t=0时,s合上,求i(t)。RRRi(t)i(t)+isrDUsDUsRRRRedistTReq(c)(a)(b)(d)图13-4例13-4图解:(1)i(0_)=i(0.)=0A(2)s合上后,从L两端求诺顿等效电路。分别由图13-4(b)、(c)可以求得:RU.L2L1,ReT2ReqRRRU,5(1--e2)A(t≥0)(3)ieR例13-5在如图所示的电路中,换路前电路已处于稳态,t=0时,s合上,求uc。3030606062+ReqUu, (0_)1F6020y20113V010V30(d)(a)(b)(c)图13-5例13-5图107
电路习题集 第十三章 一阶电路 107 例 13-3 在 t=0 时,图 13-3(a)中 s 打开,求 uc。 图 13-3 例 13-3 图 解:(1) (0 ) (0 ) uc − = uc + =0V (2)换路后,从 C 两端求戴维南等校电路,将电路化简成 RC 模型电路,如图 13-3(d) 分别由图 13-3(b)、(c)可以求得: uoc = RI s , Req = 2R (3) 2 , ( ) (1 ) (1 ),( 0) 2 = = = − = − − − R C RC u t u e RI e t RC t s t eq c oc 例 13-4 图中,t=0 时,s 合上,求 i(t)。 图 13-4 例 13-4 图 解:(1) (0 ) (0 ) L − = L + i i =0A (2) s 合上后,从 L 两端求诺顿等效电路。分别由图 13-4(b)、(c)可以求得: R L R R L R R U I eq eq s sc 2 , 2 = , = = = (3) = (1− ) = (1− 2 ) ,( 0) − − e A t R U i I e t L R s t L s c 例 13-5 在如图所示的电路中,换路前电路已处于稳态,t=0 时,s 合上,求 uc。 图 13-5 例 13-5 图

电路习题集第十三章一阶电路解:本题求解全响应,可以用三要素法。(1)0_等校电路如图13-5(b),则:u.(0_)=u.(0)=20v3×6=22,(2)利用图13-5(c)求的:R所以:T=R.C=2s3+6(3)利用0等校电路如图13-5(a),则:u(0)=3×210+10=4%v3+6(4)利用三要素公式可得:u。 = u.()+[u, (0, )- u.(o0)]e ~ 6.67(2 + e-0.5r)V,(t≥ 0)例13-6在图13-6(a)中,R=82,R=82,R=162,L=1H,求:在(0)V作用下的单位阶跃响应i,(t)及在8(t)作用下的单位冲击响应i,(t)。R2R2R2i(t)i1(0o)R1R1R1R3R3R3ReqDUsDUs(b)(c)(a)图13-6例13-6图解:(1)单位解跃响应就是在Us=ε(t)时的零状态响应i(t)。L_1U,- ε(t)_ 1(R, +R2)×R,3=82,TR..(t)A单位阶s,i,(co)ReaR, + R, + R,8R+R8+816+_二(1-e-")e(1)A跃响应为:i,(t)=i,(o)+[i,()-i,(o0)]e16(2)单位冲击响应就是在Us=8(t)时的零状态响应i,(t)。dl8r)s(t))63t(t)A此时,i(l)dt2四习题13-1开关s闭合以前电路已经稳定,求s闭合后的u(O.)i(O.),i(O,),iO.)13-2开关s闭合以前电路已经稳定,求s闭合后的i(0.),i(0.),u,(0.)。108
电路习题集 第十三章 一阶电路 108 解:本题求解全响应,可以用三要素法。 (1) − 0 等校电路如图 13-5(b),则: (0 ) (0 ) uc − = uc + =20V (2)利用图 13-5(c)求的: = + = 2 3 6 3 6 Req , 所以: R C s = eq = 2 (3)利用 等校电路如图 13-5(d),则: uc V 3 40 10 3 6 20 10 ( ) 3 + = + − = (4)利用三要素公式可得: ( ) [ (0 ) ( )] 6.67(2 ) ,( 0) 0.5 = + − + − − + u u u u e e V t t t c c c c 例 13-6 在图 13-6(a)中, R1 = 8,R2 = 8,R3 =16, L =1H ,求:在 (t) V 作用下的单位阶跃响应 i (t) L 及在 (t) 作用下的单位冲击响应 i (t) L 。 图 13-6 例 13-6 图 解:(1)单位解跃响应就是在 Us= (t) 时的零状态响应 i (t) L 。 t A t R R U s i R L R R R R R R R s L eq eq ( ) 16 1 8 8 ( ) , ( ) 8 1 8 , ( ) 1 2 3 1 2 1 2 3 = + = + = = = = + + + = 单位阶 跃响应为: i t i i i e e t A t t L L L L (1 ) ( ) 16 1 ( ) ( ) [ (0 ) ( )] 8 − − = + + − = − (2)单位冲击响应就是在 Us= (t) 时的零状态响应 i (t) L 。 此时, e t A dt d e t i t t t L ( ) 2 1 (1 ) ( )] 16 1 [ ( ) 8 8 − − = − = 四 习题 13-1 开关 s 闭合以前电路已经稳定,求 s 闭合后的 (0 ), (0 ), (0 ), (0 ) c + 1 + 2 + c + u i i i 。 13-2 开关 s 闭合以前电路已经稳定,求 s 闭合后的 (0 ), (0 ), (0 ) :L + + uL + i i

电路习题集第十三章一阶电路12(t)i1(t)4k2Si(t)60441i(t+SD12VD10VTuc(t)2k0ic(t)题13-1图题13-2图13-3t=0时,s合上,开关s闭合以前电路已经处于稳态,求s合上后的uc。13-4t=0时,s打开,开关s打开以前电路已经处于稳态,求s打开后的t=0时,s合上,开关s闭合以前电路已经处于稳态,求s合上后的i(t)。13-5t=0时,s合上,开关s闭合以前电路已经处于稳态,求s合上后的uc。3KQ3KQit(t)100i(t)最S+-610A150uc(t)126V32Vu.(t)1H1001FT-L.n题13-3图题13-4图题13-5图13-6s在1处已久,t=0时合向2,求换路后的i(t)和u,(t)。13-7电路原来已经稳定,t=0时,s打开,求换路后的uc及i。13-8电路原来已经稳定,t=0时,s由a置向b,求换路后的i(t),i(t)。5002100151HI,(t)sAS00i(t)+i(t)i(t)+u(t)uc(t)40150D15V0.10V024V0.H30TuF4010002题13-6图题13-7图题13-8图13-9已知:I=10mAR,=6K2,R,=3KQ,R=2K2,C=5uF,电路原来已经稳定,t=0时,s合上,求s合上后的u(t),i(t)。13-10电路原来已经稳定,t=0时,s打开,求换路后的u,(t)。13-11已知:U=2V,R=1Q,R,=R,=22,L=2H,电路原来已经稳定,=0时,s合向2,求换路后的(t)。109
电路习题集 第十三章 一阶电路 109 题 13-1 图 题 13-2 图 13-3 t=0 时,s 合上,开关 s 闭合以前电路已经处于稳态,求 s 合上后的 uc。 13-4 t=0 时,s 打开,开关 s 打开以前电路已经处于稳态,求 s 打开后的 t=0 时,s 合上, 开关 s 闭合以前电路已经处于稳态,求 s 合上后的 i (t) L 。 13-5 t=0 时,s 合上,开关 s 闭合以前电路已经处于稳态,求 s 合上后的 uc。 题 13-3 图 题 13-4 图 题 13-5 图 13-6 s 在 1 处 已久,t=0 时合向 2,求换路后的 i (t) L 和 u (t) L 。 13-7 电路原来已经稳定,t=0 时,s 打开,求换路后的 uc 及 i。 13-8 电路原来已经稳定,t=0 时,s 由 a 置向 b,求换路后的 i (t),i(t) L 。 题 13-6 图 题 13-7 图 题 13-8 图 13-9 已知: I s =10mA,R1 = 6K,R2 = 3K,R3 = 2K,C = 5F ,电路原来已经稳定, t=0 时, s 合上,求 s 合上后的 u (t),i (t) c c 。 13-10 电路原来已经稳定,t=0 时, s 打开,求换路后的 u (t) L 。 13-11 已知: Us = 2V,R1 =1,R2 = R3 = 2, L = 2H ,电路原来已经稳定,t=0 时, s 合 向 2,求换路后的 i (t) L