
电路习题集第八章正弦稳态电路的分析第八章正弦稳态电路的分析.基本要求1.掌握阻抗(导纳)的概念及其串并联化简。2.能将直流电路的各种分析方法应用到相量法中,来分析计算正弦交流电路。3.掌握正弦交流电路中各种功率的概念。4.掌握RLC串、并联电路的谐振条件及频率特性。二.本章要点1.R、L、C串联电路的阻抗11Z=R+ioL+=R+(oL-)=R+i(XL +Xc)=R+iX=|ZZΦjocOCI[z] 感抗XL=OL,容抗XcXoc当X=XL-Xc>0,感性电路,电压超前电流;Φ广R当X=X-Xc<0,容性电路,电压落后电流。图8-1阻抗三角形2.R、L、C并联电路的导纳[Y]B11Y=+joC=G+i(Bc+BL)=G+jB=YZΦRjoLTd-G1感纳BL=容纳Bc=0C图8-2导纳三角形OL3.无源一端口的阻抗、导纳、功率uU+阻抗:7-Z(-)=Z/Z0T"T0Noi1导纳:Y=(-)=00TU阻抗和导纳互为倒数关系Z=图8-3无源一端口Y有功功率:P=UIcosΦS无功功率:Q=UIsinΦQ视在功率:S=UITd复功率:S=ui=P+joPcosΦ叫做电路的功率因数图8-4功率三角形61
电路习题集 第八章 正弦稳态电路的分析 61 第八章 正弦稳态电路的分析 一. 基本要求 1.掌握阻抗(导纳)的概念及其串并联化简。 2.能将直流电路的各种分析方法应用到相量法中,来分析计算正弦交流电路。 3.掌握正弦交流电路中各种功率的概念。 4.掌握 RLC 串、并联电路的谐振条件及频率特性。 二.本章要点 1. R 、 L、C 串联电路的阻抗 ) j( L C) j Z 1 j( j 1 j R X X R X Z Φ C R L C Z = R + L + = + − = + + = + = 感抗 XL =L ,容抗 C X 1 C = 当 X = XL − XC 0 , 感性电路,电压超前电流; 当 X = XL − XC 0 , 容性电路,电压落后电流。 图 8-1 阻抗三角形 2. R 、 L、C 并联电路的导纳 j j( C L ) j Y j 1 1 C G B B G B Y Φ R L Y = + + = + + = + = 感纳 L 1 L B = ,容纳 BC =C 图 8-2 导纳三角形 3.无源一端口的阻抗、导纳、功率 阻抗: (Ψ Ψ ) Z ΦZ I U I U Z = = u − i = 导纳: (Ψ Ψ ) Y ΦY U I U I Y = = i − u = 阻抗和导纳互为倒数关系 Y 1 Z = 图 8-3 无源一端口 有功功率: P =UI cosΦ 无功功率: Q =UIsinΦ 视在功率: S =UI 复功率: S =UI = P + jQ cosΦ 叫做电路的功率因数 图 8-4 功率三角形

电路习题集第八章正弦稳态电路的分析4.对于感性负载,当功率因数cosΦ比较低时,可以采用并联电容的方法提高功率因数。5.阻抗的串联与并联n个阻抗串联:Z=Z+Z2+..Z.111n个阻抗并联:或者Yeg=Yi+Y2+...YnZeqZZ,Z.Z,Z22个阻抗并联:ZeZ + Z2Z2Zii:i,=分流公式:1Z+Z2Z +Z2i0lilie+0ZiZe10图8-52个阻抗并联6.应用相量法,并引入阻抗与导纳后,直流电路中的各种定律,定理及分析计算方法都可以推广应用到正弦交流电路。7.含有电容、电感的电路,当电抗或电纳等于零,电压和电流同相时,电路发生谐振。谐振时电路呈电阻性,谐振电路对不同频率的信号具有选择性。电路的品质因数Q对谐振曲线形状的影响很大。8.负载阻抗Z,和电源内阻抗Z为共轭复数时,称为最佳匹配,此时负载可获得最大功率。三.典型例题例8-1写出图示电路的输入阻抗Z,表达式,の已知,不必化简。RiR2R2aoaoRiL3C=C:L3bobo(a)(b)图 8-6例8-1图1x(R2 + joL)(R + joL)×(R2解:(a) Zab=R+ joc100(b) Za11+(R2 + joL)(R + joL)+(R2 +jocjoc62
电路习题集 第八章 正弦稳态电路的分析 62 4.对于感性负载,当功率因数 cosΦ 比较低时,可以采用并联电容的方法提高功率因数。 5.阻抗的串联与并联 n 个阻抗串联: Zeq = Z1 + Z2 +Zn n 个阻抗并联: 1 1 1 1 Zeq Z1 Z2 Zn = + ++ 或者 Yeq =Y1 +Y2 +Yn 2 个阻抗并联: 1 2 1 2 eq Z Z Z Z Z + = 分流公式: I Z Z Z I 1 2 2 1 + = ; I Z Z Z I 1 2 1 2 + = 图 8-5 2 个阻抗并联 6.应用相量法,并引入阻抗与导纳后,直流电路中的各种定律,定理及分析计算方法都可 以推广应用到正弦交流电路。 7.含有电容、电感的电路,当电抗或电纳等于零,电压和电流同相时,电路发生谐振。谐 振时电路呈电阻性,谐振电路对不同频率的信号具有选择性。电路的品质因数 Q 对谐振曲 线形状的影响很大。 8.负载阻抗 Z L 和电源内阻抗 Zeq 为共轭复数时,称为最佳匹配,此时负载可获得最大功率。 三.典型例题 例 8-1 写出图示电路的输入阻抗 Zab 表达式, 已知,不必化简。 (a) (b) 图 8-6 例 8-1 图 解:(a) ( j ) j 1 ( j ) j 1 2 2 ab 1 R L C R L C Z R + + + = + ;(b) ) j 1 ( j ) ( ) j 1 ( j ) ( 1 2 1 2 ab C R L R C R L R Z + + + + + =
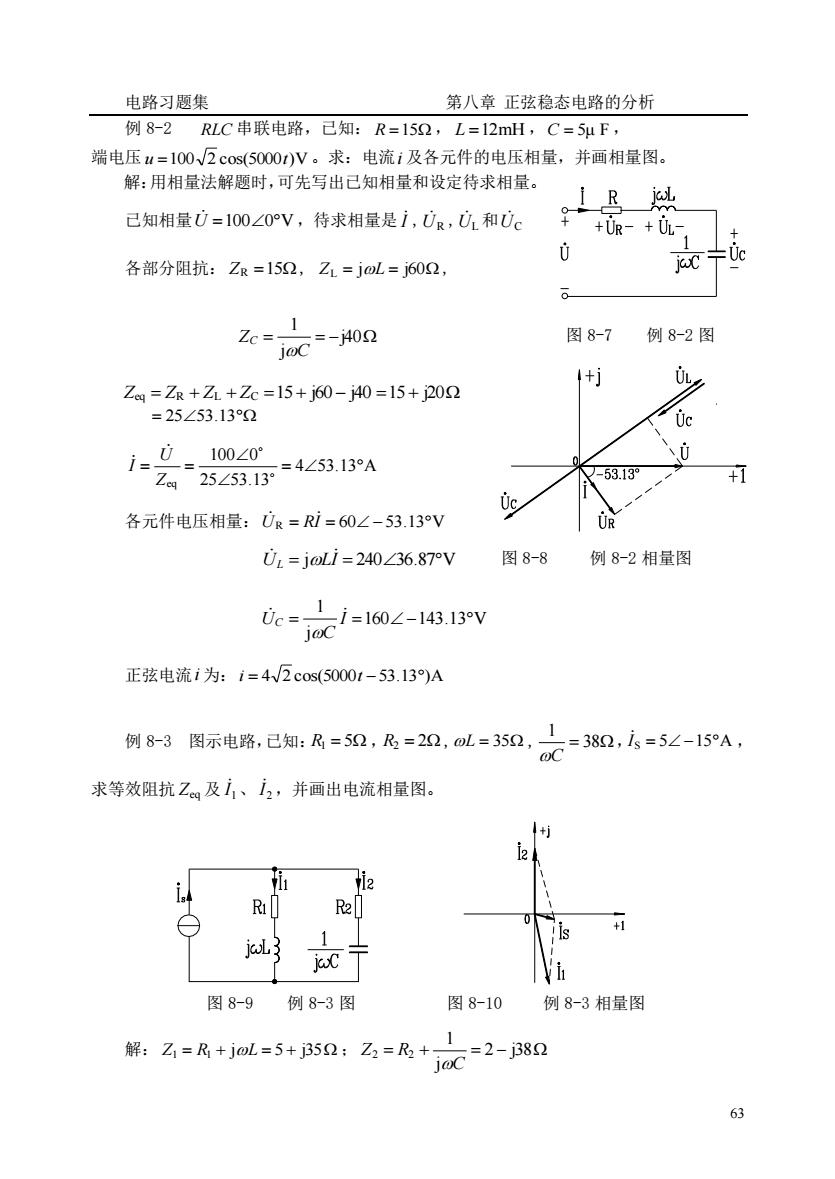
电路习题集第八章正弦稳态电路的分析例 8-2 RLC串联电路,已知:R=15Q,L=12mH,C=5uF,端电压u=100/2cos(5000t)V。求:电流i及各元件的电压相量,并画相量图。解:用相量法解题时,可先写出已知相量和设定待求相量。iRjal+已知相量U=100Z0V,待求相量是i,UR,U,和U。+UR- + UL-0Ucjac各部分阻抗:ZR=15Q,ZL=joL=j60Q,01图 8-7例8-2图Zc:-j402joc.5I+jZeg=ZR+ZL+Zc=15+j60-j40=15+j20Q=25/53.13°Q2UcUi=0100Z0°=4/53.13°A+153.13°Zeq25Z53.13°Uo各元件电压相量:UR=Ri=60Z-53.13VURU, =joLi=240Z36.87V图 8-8例8-2相量图i=160Z-143.13°VUc:joc正弦电流i为:i=4/2cos(5000t-53.13)A例8-3图示电路,已知:R=52,R,=2Q,0L=352=382,is=5/-15°A,oC求等效阻抗Ze.及i、i,,并画出电流相量图。I+ji2 iii2iRiR2[+1lis1jcL3jccii图8-9例8-3图图8-10例8-3相量图1解:Z=R+joL=5+j35Q:Z,=R22-38Qjoc63
电路习题集 第八章 正弦稳态电路的分析 63 例 8-2 RLC 串联电路,已知: R =15 , L =12mH ,C = 5μ F , 端电压 u =100 2 cos(5000t)V 。求:电流 i 及各元件的电压相量,并画相量图。 解:用相量法解题时,可先写出已知相量和设定待求相量。 已知相量 U =1000V ,待求相量是 I ,UR ,UL 和 UC 各部分阻抗: ZR =15, ZL = jL = j60 , = = −j40 j 1 C ZC 图 8-7 例 8-2 图 Zeq = ZR + ZL + ZC =15 + j60 − j40 =15 + j20 = 2553.13 4 53.13 A 25 53.13 100 0 eq = = = Z U I 各元件电压相量: U R = RI = 60 − 53.13V U L = jLI = 24036.87V 图 8-8 例 8-2 相量图 160 143.13 V j 1 = I = − C UC 正弦电流 i 为: i = 4 2 cos(5000t −53.13)A 例 8-3 图示电路,已知: R1 = 5 ,R2 = 2,L = 35 , = 38 1 C ,I S = 5 −15A , 求等效阻抗 Zeq 及 1 I 、 2 I ,并画出电流相量图。 图 8-9 例 8-3 图 图 8-10 例 8-3 相量图 解: Z1 = R1 + jL = 5 + j35 ; = + = 2 − j38 j 1 2 2 C Z R

电路习题集第八章正弦稳态电路的分析Z.Z2(5+ j35)(2 - j38)=176.7Z18.08°2Zeq=-Z + Z25+j35+2-j382- j38Z2is分流公式:i×5-15°=24.98/-78.79°A;Z, + Z25+j35+2-j38Zi5 + j35is=i2 =x5/-15°=23.20/90.26°AZ +Z25+j35+2-j38相量图见图8-10例8-4图8-11所示电路,试列出该电路的节点电压方程及网孔电流方程。21 0 Za +is- ?Z5-Lis5+Usiz2iZ4m)?图8-11例8-4图解:1.节点电压方程,以节点③为参考节点。UstUs31111JUalU.节点①:ZZ2Z3Z3ZiZ3Us + issL_Unl(1+一0节点②:Z3Z3Z4Z3注意:节点法中,与电流源串联的阻抗应略去,自导、互导中均不应出现。2.网孔电流方程网孔①:(Z+Z)im-Zim=Us网孔?:-Z,im+(Z,+Z+Z4)im-Z4im=-Us3网孔③:im=-iss例8-5图8-12中。试列出该电路的节点电压方程和网孔电流方程。解:此电路有无伴电压源和无伴受控电流源。(1)列节点电压方程。令节点②为参考节点,对节点①③④列出下列方程:节点①:U=Us264
电路习题集 第八章 正弦稳态电路的分析 64 = + + + = + = 176.7 18.08 5 j35 2 - j38 (5 j35)(2 - j38) 1 2 1 2 eq Z Z Z Z Z 分流公式: 5 15 24.98 78.79 A 5 j35 2 - j38 2 - j38 S 1 2 2 1 − = − + + = + = I Z Z Z I ; 5 15 23.20 90.26 A 5 j35 2 - j38 5 j35 S 1 2 1 2 − = + + + = + = I Z Z Z I 相量图见图 8-10 例 8-4 图 8-11 所示电路,试列出该电路的节点电压方程及网孔电流方程。 图 8-11 例 8-4 图 解:1.节点电压方程,以节点③为参考节点。 节点①: 1 ) 1 1 1 ( 3 S3 1 S1 n2 3 n1 1 2 3 Z U Z U U Z U Z Z Z + + − = + 节点②: S5 3 S3 n2 3 4 n1 3 Z ) Z 1 Z 1 ( Z 1 I U U U − − + = − + 注意:节点法中,与电流源串联的阻抗应略去,自导、互导中均不应出现。 2.网孔电流方程 网孔①: (Z1 Z2 )Im1 Z2Im2 US1 + − = 网孔②: Z2Im1 (Z2 Z3 Z4 )Im2 Z4Im3 US3 − + + + − = − 网孔③: Im3 IS5 = − 例 8-5 图 8-12 中。试列出该电路的节点电压方程和网孔电流方程。 解:此电路有无伴电压源和无伴受控电流源。 (1) 列节点电压方程。令节点②为参考节点,对节点①③④列出下列方程: 节点①: Un1 US2 =
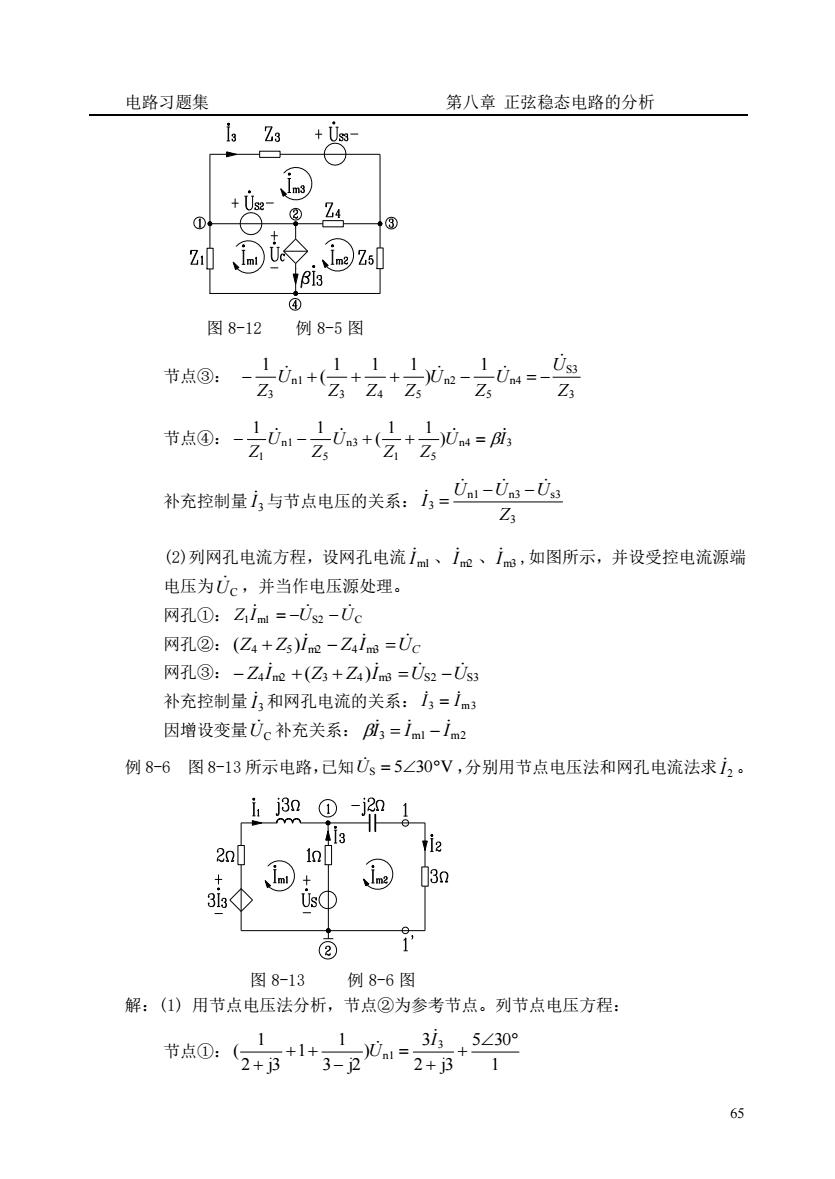
电路习题集第八章正弦稳态电路的分析isZ3m3+UsZ42CUim2)Z5Zilpis?图8-12例8-5图1Us31节点③:LIZ3Z.ZsZsZ3Z3111Un4=BiT节点④:Z.ZsZ,ZsUn-Un-Us补充控制量i,与节点电压的关系:i;=Z3(2)列网孔电流方程,设网孔电流iml、im、im,如图所示,并设受控电流源端电压为Uc,并当作电压源处理。网孔:Zim=-Us2-Uc网孔②:(Z4+Z)im-Zim=U网孔③:-Z4im+(Z+Z)im=Us2-Us补充控制量i,和网孔电流的关系:1,=im3因增设变量Uc补充关系:Bi,=iml-im2例8-6图8-13所示电路,已知Us=5Z30°V,分别用节点电压法和网孔电流法求i2。ij3n-jn4i3i22nl1niml30Usd3i3<16图8-13例8-6图解:(1)用节点电压法分析,节点②为参考节点。列节点电压方程:3i,5Z30°节点①:IL2 + j33.22+ j3165
电路习题集 第八章 正弦稳态电路的分析 65 图 8-12 例 8-5 图 节点③: 3 S3 n4 5 n2 3 4 5 n1 3 1 ) 1 1 1 ( 1 Z U U Z U Z Z Z U Z − + + + − = − 节点④: n4 3 1 5 n3 5 n1 1 ) 1 1 ( 1 1 U I Z Z U Z U Z − − + + = 补充控制量 3 I 与节点电压的关系: 3 n1 n3 s3 3 Z U U U I − − = (2)列网孔电流方程,设网孔电流 m1 I 、 m2 I 、 m3 I ,如图所示,并设受控电流源端 电压为 UC ,并当作电压源处理。 网孔①: Z1Im1 US2 UC = − − 网孔②: Z Z I Z I UC + − = ( 4 5 ) m2 4 m3 网孔③: Z4Im2 (Z3 Z4 )Im3 US2 US3 − + + = − 补充控制量 3 I 和网孔电流的关系: I3 Im3 = 因增设变量 UC 补充关系: I3 Im1 Im2 = − 例 8-6 图 8-13 所示电路,已知 U S = 530V ,分别用节点电压法和网孔电流法求 2 I 。 图 8-13 例 8-6 图 解:(1) 用节点电压法分析,节点②为参考节点。列节点电压方程: 节点①: 1 5 30 2 j3 3 ) 3 j2 1 1 2 j3 1 ( 3 n1 + + = − + + + I U