
电路习题集第十五章动态电路的复频域求解第十五章动态电路的复频域求解一本章要求1:,握拉普拉斯变换,拉普拉斯反变换(部分分式展开法)。2.握电路定律及各电路元件的复频域形式。3.:握运算阻抗、运算导纳等概念。4.电路的复频域分析法。二内容提要1.时间函数f(t)的拉普拉斯变换F(s) = LLf(t)= [f(t)e-"di(15-1)F(s)为f(t)得像函数,f(t)为F(s)的原函数,S=α+jの为复频率。2.拉普拉斯变换的性质(15-2)a)线性性质L[af(t)+bf,(t))=aF(s)+bF,(s)延迟性质L[f(t-t)e(t-t.)]=e-sF(s)(15-3)b)((]= sF(s)- f(0.)微分性质L(15-4)c)dt["f(t)dt = F(s)/ s积分性质L[(15-5)d)3.普拉斯反变换,部分分式展开法N(s)bms"+bm-,sm-+..+b,s+b.为假分式时,则利用长除法先转化当F(s)=D(s)a,s"+a,s"--+...+as+ao为整式加真分式,再求f(t)。当F(s)为真分式时,n>m。1)D(s)=0有Pl,P2"-P个实单根时,则N'(p.)F(s)=_4N()JIs= P或 AkA, =[(s-Pk)D(s)D(pk)s-Pk则 f(1)=A,eP(15-6)2)D(s)=0有一对共轭根pi=α+jo,P2=α-jの,则118
电路习题集 第十五章 动态电路的复频域求解 118 第十五章 动态电路的复频域求解 一 本章要求 1. 握拉普拉斯变换,拉普拉斯反变换(部分分式展开法)。 2. 握电路定律及各电路元件的复频域形式。 3. 握运算阻抗、运算导纳等概念。 4. 电路的复频域分析法。 二 内容提要 1. 时间函数 f(t)的拉普拉斯变换 F s L f t f t e dt st − − = = 0 ( ) [ ( )] ( ) (15-1) F(s)为 f(t)得像函数,f(t)为 F(s)的原函数, s = + j 为复频率。 2.拉普拉斯变换的性质 a) 线性性质 [ ( ) ( )] ( ) ( ) 1 2 1 2 L af t + bf t = aF s + bF s (15-2) b) 延迟性质 [ ( ) ( )] ( ) 0 0 0 L f t t t t e F s −st − − = (15-3) c) 微分性质 ] ( ) (0 ) ( ) [ = − − sF s f dt df t L (15-4) d) 积分性质 L f t dt F s s t [ ( ) ( )/ 0 = − (15-5) 3. 普拉斯反变换,部分分式展开法 当 1 0 1 1 0 1 1 ( ) ( ) ( ) a s a s a s a b s b s b s b D s N s F s n n n n m m m m + + + + + + + + = = − − − 为假分式时,则利用长除法先转化 为整式加真分式,再求 f(t)。 当 F(s)为真分式时,n>m。 1〉 D(s)=0 有 p1 p2 pk , 个实单根时,则 k k k n k k k s p D s N s A s p s p A F s = − = − = = ]| ( ) ( ) ( ) , [( ) 1 或 ( ) ( ) k k k D p N p A = 则 = = n k p t k k f t A e 1 ( ) (15-6) 2〉 D(s)=0 有一对共轭根 p1 = + j, p2 = − j ,则
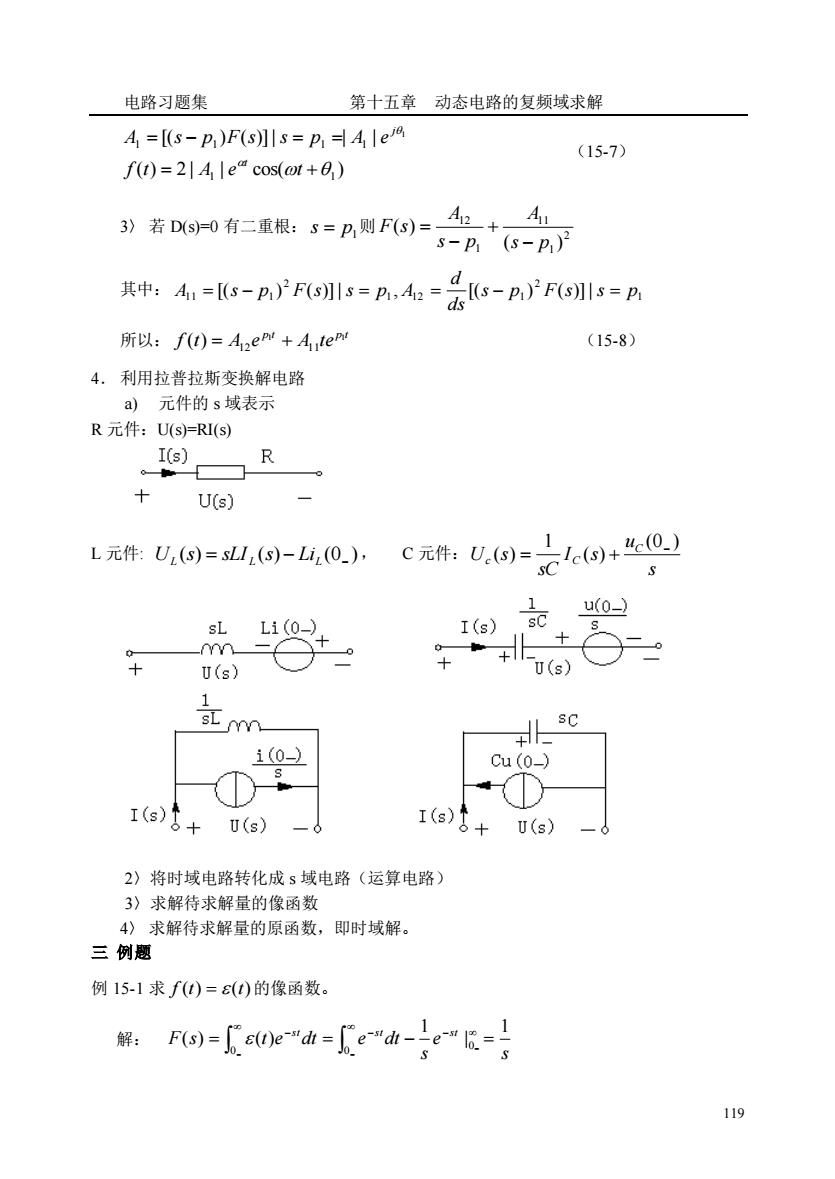
电路习题集第十五章动态电路的复频域求解A =[(s - p))F(s)]/ s= p, =| A, Iejo(15-7)f(t) = 2/ A /e cos(ot +@)A,A123)若D(s)=0有二重根:S=P,则F(s)=s-p(s-p)dr其中: A, =[(s-p,)"F(s)]|s= pl,Ai2 =-[(s-p)"F(s)]/s= pids所以:f(t)=AzeP+A,tepr(15-8)4.利用拉普拉斯变换解电路a)元件的s域表示R元件:U(s)=RI(s)I(s)RoJo+U(s)ucoL元件:U,(s)=sLI,(s)-Li,(O_),C元件:U.(s)sCS1u(o_)sCsLI(s)SLi(0o_)+Xn+U(s)+U(s)1SLsCi(0)Cu (o-).I(s)1I(s)U(s)U(s)+2)将时域电路转化成s域电路(运算电路)3)求解待求解量的像函数4》求解待求解量的原函数,即时域解。三例题例15-1求f(t)=ε(t)的像函数。F(s) = [e(t)e-" dt = ["e-" dt - I5t10解:.119
电路习题集 第十五章 动态电路的复频域求解 119 ( ) 2 | | cos( ) [( ) ( )]| | | 1 1 1 1 1 1 1 = + = − = = f t A e t A s p F s s p A e t j (15-7) 3〉 若 D(s)=0 有二重根: p1 s = 则 2 1 11 1 12 ( ) ( ) s p A s p A F s − + − = 其中: 1 2 1 1 2 1 2 1 1 1 [( ) ( )]| , [(s p ) F(s)]| s p ds d A = s − p F s s = p A = − = 所以: p t p t f t A e A te 1 1 12 11 ( ) = + (15-8) 4. 利用拉普拉斯变换解电路 a) 元件的 s 域表示 R 元件:U(s)=RI(s) L 元件: ( ) ( ) (0 ) L = L − LiL − U s sLI s , C 元件: s u I s sC U s C c C (0 ) ( ) 1 ( ) − = + 2〉将时域电路转化成 s 域电路(运算电路) 3〉求解待求解量的像函数 4〉 求解待求解量的原函数,即时域解。 三 例题 例 15-1 求 f (t) = (t) 的像函数。 解: s e s F s t e dt e dt st st st 1 | 1 ( ) ( ) 0 0 0 = = − = − − − − − −

电路习题集第十五章动态电路的复频域求解例15-2已知:f(t)如图15-1所示,求F(s)。+ft)解:2f(t) = 2s(t) -ε(t- 2)-s(t - 4)232-43ee-.:. F(s)21o42ssss图15-1例15-2图s+4例15-3已知:F(s) =求原函数f(t)。s(s + 1)(s +2)解:+AA2A +F(s) =$+1s+2sS+4S+41s=0 = 2A, = sF(s)Is=0= sS s(s + 1)(s+2) 0= (s+1)(s +2)A, =(s +1)F(s)/s--=-3A, =(s + 2)F(s) /-,= 12..31.. F(s)= 3,f(t)=2-3e-t +e-21s$+1+s+2'S +2例15-4已知:F(s)=2,求原函数f(t)。s2+2s+2解s2+2s+2=0= p =-1+ j1,p, =-1- jlV2-45°A, =(s +1- J)F(s) Is=-+1 =2:. f(10 = /2e' cos(t - 45°)7s+8例15-5 已知F(s)=求原函数f(t)。s(s + 1)(s + 2)2解:A31F(s)=4+4+42 +-$+1$+2(s+2)2SA, = sF(s) I=0= 2, A2 = (s+1)F(s) /=-I= -1d[(s + 2)* F(s)] 1=-2= -1, A3 = (s + 2)* F(s) /s=-2 = -3A32ds.. f(t)=2-e-t-e-2t-3te-2r120
电路习题集 第十五章 动态电路的复频域求解 120 例 15-2 已知:f(t)如图 15-1 所示,求 F(s)。 解: (2 ) 2 1 ( ) ( ) 2 ( ) ( 2) ( 4) 2 4 2 4 s s s s e e s s e s e s F s f t t t t − − − − = − − = − − = − − − − 图 15-1 例 15-2 图 例 15-3 已知: ( 1)( 2) 4 ( ) + + + = s s s s F s ,求原函数 f(t)。 解: t t s s s s s f t e e s s s F s A s F s A s F s s s s s s s s A sF s s s A s A s A F s 2 3 2 2 1 1 0 0 0 1 2 3 , ( ) 2 3 2 1 1 2 3 ( ) ( 2) ( ) | 1 ( 1) ( ) | 3 | 2 ( 1)( 2) 4 | ( 1)( 2) 4 ( ) | 1 2 ( ) − − =− =− = = = = − + + + + = − = + = = + = − = + + + = + + + = = + + + = + 例 15-4 已知: 2 2 2 ( ) 2 + + + = s s s F s ,求原函数 f(t)。 解 ( 0 2 cos( 45 ) 45 2 2 ( 1 ) ( ) | 2 2 0 1 1, 1 1 1 1 1 1 2 2 t o o s j f t e t A s j F s s s p j p j = − = + − = − + + = = − + = − − − =− + 例 15-5 已知 2 ( 1)( 2) 7 8 ( ) + + + = s s s s F s ,求原函数 f(t)。 解: t t t s s s s f t e e t e s F s A s F s ds d A A sF s A s F s s A s A s A s A F s 2 2 2 2 2 31 2 32 1 0 2 1 2 1 2 32 31 ( ) 2 3 [( 2) ( )]| 1, ( 2) ( ) | 3 ( ) | 2, ( 1) ( ) | 1 1 2 ( 2) ( ) − − − =− =− = =− = − − − = + = − = + = − = = = + = − + + + + + = +

电路习题集第十五章动态电路的复频域求解例15-6电路如图15-2(a)所示,电路已达到稳态,t=0时,s打开,已知:Is=10AR=R=402,L=4H,C=0.01F,求:s打开后的uc。解:1)0_等效电路如图15-2(b)所示,则R,I,=5A,uc(0_)=R,i,(0_)=40×50=200Vi(0_):R, +R,2)t≥0,后,运算电路如图15-2(c)400其中: U,(s)= L[1,R]=L[10×40]= 4由:1 (s)+ uc(0.)-U.(s)+R,I,(s)+ sLI,(s)- Li,(O_)+sCs400200U, (s) + Li; (0.) - uc(0.)F4x55s+50SSs. I(s) =R +$L+1s2+10s+2540+4s +sC0.01s15s + 502001uc(o_)1,(s)+KVLUc(s) =0.01ss2+10s+25sCss400500200$+5s(s + 5)2:.uc(t)=400-500te-5tt-200e-5V,t≥0iir(0)R2R2Lit(0) i()sLo01LLsCXXR1uc(0)cTuc(t)R1R1u(o_)I-[Js (s)(a)(b)(c)图15-2例15-6图例15-7如图15-3(a)所示的电路原来已处于稳态,t=0时,s闭合,用运算法求s和上后的i,(t)。解:1)0_等效电路如图15-3(b)所示,则i(0_)=0,uc(0_)=U, = 1Vb)运算电路如图15-3(c),列回路方程121
电路习题集 第十五章 动态电路的复频域求解 121 例 15-6 电路如图 15-2(a)所示,电路已达到稳态,t=0 时,s 打开,已知: Is =10A,R1 = R2 = 40,L = 4H,C = 0.01F ,求:s 打开后的 C u 。 解:1〉 − 0 等效电路如图 15-2 (b)所示,则 I A u R i V R R R i L (0 ) s 5 , C (0 ) 2 L (0 ) 40 50 200 1 2 1 = = = = + − = − − 2〉 0+ t 后,运算电路如图 15-2(c) 其中: s Us s L I sR L 400 ( ) [ ] [10 40] = 1 = = 由: KVL ( ) 400 500 200 , 0 5 200 ( 5) 400 500 200 10 25 5 50 0.01 (0 ) 1 ( ) 1 ( ) 10 25 5 50 0.01 1 40 4 200 4 5 400 1 (0 ) ( ) (0 ) ( ) 0 (0 ) ( ) 1 ( ) ( ) ( ) (0 ) 5 5 2 2 2 1 1 = − − + − + = − + + + + = + = + + + = + + + − = + + + − = − + + − + + = − − − − − − − u t t e e V t s s s s s s s s s u I s sC U s s s s s s s s sC R sL s u U s Li I s s u I s sC U s R I s sLI s Li t t C C C L C s L L C s L L L L 图 15-2 例 15-6 图 例 15-7 如图 15-3 (a) 所示的电路原来已处于稳态,t=0 时,s 闭合,用运算法求 s 和上后 的 ( ) 1 i t 。 解:1〉 − 0 等效电路如图 15-3 (b)所示,则 i 1 (0− ) = 0,uC (0− ) = Us =1V b) 运算电路如图 15-3 (c),列回路方程
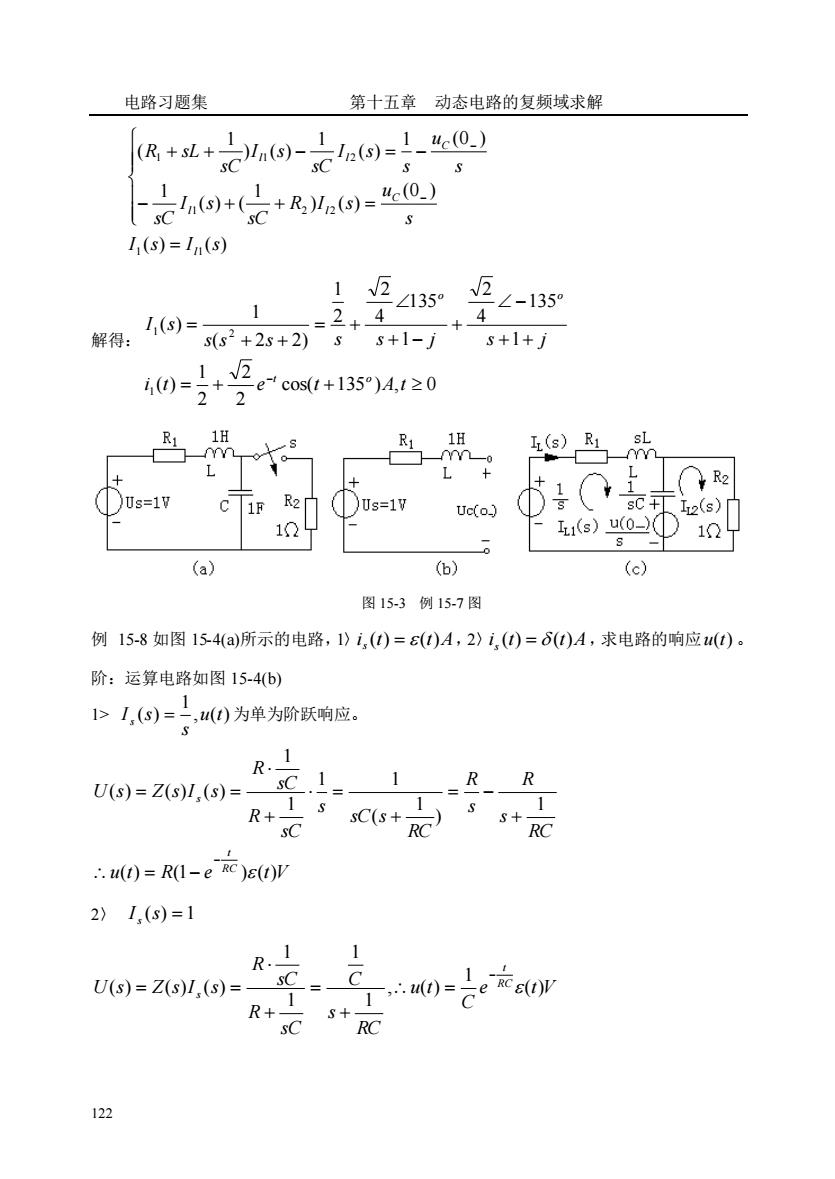
电路习题集第十五章动态电路的复频域求解 /2(s) =1_ "c(0.)1(R, +sL +)n(s)sCssuc(0_)+ R,)2(s)= In(s)+(SCsCsI,(s) = In(s)V2/21Z135°-135°2144I(s)=s(s2 +2s + 2)解得:ss+1-js+1+ j/21i,(t) =cos(t+135°)A,1≥0221HRi1HsLR1RI(s)Smmm01LXLL.OR2X1R2DUs=1VC)Us=1VsC+1FI2(s)SUc(o.)ILi(s)u(o_d10210519(a)(b)(c)图15-3例15-7图例15-8如图15-4(a)所示的电路,1)i.(t)=ε(t)A,2)i(t)=8(t)A,求电路的响应u(t)。阶:运算电路如图15-4(b)11> I.(s),u(t)为单为阶跃响应。s1R.1RR1SCU(s) = Z(s)/.(s) =11ssR+sC(s +s+RCSCRC.. u(t)= R(1-e RC)e(t)VI,(s)=12)11-CR.I1sC-eRCe(t)VU(s) = Z(s)I,(s) :..u(t)11CR+s+RCsC122
电路习题集 第十五章 动态电路的复频域求解 122 ( ) ( ) (0 ) ) ( ) 1 ( ) ( 1 1 (0 ) ( ) 1 ) ( ) 1 ( 1 1 1 2 2 1 1 2 I s I s s u R I s sC I s sC s u s I s sC I s sC R sL l C l l C l l = − + + = + + − = − − − 解得: cos( 135 ) , 0 2 2 2 1 ( ) 1 135 4 2 1 135 4 2 2 1 ( 2 2) 1 ( ) 1 1 2 = + + + + − + + − = + + + = − i t e t A t s s s s s j s j I s t o o o 图 15-3 例 15-7 图 例 15-8 如图 15-4(a)所示的电路,1〉 i s (t) = (t)A,2〉 i s (t) = (t)A ,求电路的响应 u(t) 。 阶:运算电路如图 15-4(b) 1> , ( ) 1 ( ) u t s I s s = 为单为阶跃响应。 u t R e t V RC s R s R RC sC s s sC R sC R U s Z s I s RC t s ( ) (1 ) ( ) 1 ) 1 ( 1 1 1 1 ( ) ( ) ( ) − = − + = − + = + = = 2〉 I s (s) = 1 e t V C u t RC s C sC R sC R U s Z s I s RC t s ( ) 1 , ( ) 1 1 1 1 ( ) ( ) ( ) − = + = + = =