
电路习题集第三章电阻电路的一般分析第三章电阻电路的一般分析一、基本要求1、学生通过学习本章会熟练运用结点电压法求解电路,包括含有理想电压源,受控源的电路。2、会运用支路电流法、网孔电流法、回路电流法求解电路,包括含有理想电流源,受控源的电路。二、本章要点本章主要介绍求解电路的一般分析方法,这种方法不要求改变电路结构。首先选择一组合适的电路变量(电流或电压),根据KCL和KVL及元件的电压、电流关系(VCR)建立该组变量的独立方程组,然后从方程组中解出电路变量。1、支路电流法:是以支路电路作为未知量的求解方法。分析电路时,对于n个结点,b条支路的电路根据KCL,列出(n-1)个结点电流方程,同时根据KVL列出m=b-(n-I)个独立回路电压方程,于是,总共得到以支路电流为未知量(即变量)的b独立方程。必须指出:如果电路的某一个支路含有恒流源则此支路电流即为该恒流源的电流,在列含有恒流源回路的电压方程时,可设恒流源的端电压U为未知量。2、网孔电流法:是以“假想网孔电流”作为独立变量求解电路的方法,称为网孔电流法。它仅使用于平面电路。对具有m个网孔的平面电路,网孔电路的一般形式有:Riiimi+R12im2+R13im3+..+R1mim=us11R21im+R22im2+R23im3+..+R2mimm=us22(3-1)Rm1im1+Rm2im2+Rm3im3+...+Rmmimm=Usmm3.回路电流法是以“假想回路电流”作为独立变量的求解电路的方法称为回路电流法。网孔电流法仅适用于平面电路.回路电流法,则无此限制它适用于平面或非平面电。对于b条支路,n个结点的电路,回路数(l=b-n+1)与网孔电流法方程(3-1)相似,可以写出回路电流方程的一般形式,有Riiin+Ri2ii2+R13ii3+...+Riii1i=us11R21i11+R22i12+R23i13+..+R2i11=us22(3-2)Rnin+Ri2i2+R13i13+..+Rnin=usi21
电路习题集 第三章 电阻电路的一般分析 21 第三章 电阻电路的一般分析 一、基本要求 1、学生通过学习本章会熟练运用结点电压法求解电路,包括含有理想电压源,受控源的 电路。 2、会运用支路电流法、网孔电流法、回路电流法求解电路,包括含有理想电流源,受控 源的电路。 二、本章要点 本章主要介绍求解电路的一般分析方法,这种方法不要求改变电路结构。首先选择一组 合适的电路变量(电流或电压),根据 KCL 和 KVL 及元件的电压、电流关系(VCR)建 立该组变量的独立方程组,然后从方程组中解出电路变量。 1、支路电流法: 是以支路电路作为未知量的求解方法。分析电路时,对于 n 个结点,b 条支路的电路 根据 KCL,列出(n-1)个结点电流方程,同时根据 KVL 列出 m=b-(n-1)个独立回路电压 方程,于是,总共得到以支路电流为未知量(即变量)的 b 独立方程。 必须指出:如果电路的某一个支路含有恒流源,则此支路电流即为该恒流源的电流, 在列含有恒流源回路的电压方程时,可设恒流源的端电压 U 为未知量。 2、网孔电流法: 是以“假想网孔电流”作为独立变量求解电路的方法,称为网孔电流法。它仅使用 于平面电路。对具有 m 个网孔的平面电路,网孔电路的一般形式有: R11im1+R12im2+R13im3+.+R1mimm=uS11 R21im1+R22im2+R23im3+.+R2mimm=uS22 . Rm1im1+Rm2im2+Rm3im3+.+Rmmimm=uSmm 3. 回路电流法 是以“假想回路电流”作为独立变量的求解电路的方法称为回路电流法。 网孔电流法仅适用于平面电路,回路电流法, 则无此限制,它适用于平面或非平面电。 对于 b 条支路,n 个结点的电路,回路数(l=b-n+1)与网孔电流法方程(3-1)相似,可 以写出回路电流方程的一般形式,有 R11il1+R12il2+R13il3+.+R1lill=uS11 R21il1+R22il2+R23il3+.+R2lill=uS22 . Rl1il1+Rl2iL2+Rl3il3+.+Rllill=uSll (3-1) (3-2)

电路习题集第三章电阻电路的一般分析(1)式(3-1)和(3-2)中有相同下标的电阻Rll.R22.R33等是各网孔和各回路的自阻,有不同下标的电阻R12.R23.R31等是各网孔和回路的互阻。(2)自阻总是正的互阻取正还是取负,则由相关的两个网孔电流和回路电流通过公共电阻时两者的参考方向是否相同来决定,相同时取正,相反时取负。显然,若两个回路和网孔间没有公共电阻则相应的互阻为零(3)方程右方的us11,us22....分别为网孔和回路1,2....等中电压源的代数和,取和时,各电压源的方向与网孔和回路电流的方向一致的电压源前应取“一”号,否则取“+”号。4.结点电压法结点电压法是以结点电压为未知量,应用KCL列出结点电流方程,然后用结点电压来表示各支路电流代入结点电流方程。一个具有(n+1)个结点,b条支路的电路当选定任一结点为参考结点后,其余的n个结点是独立的,它的结点电压方程有:Giiuni+ Gi2un+ G1un3+ **. + Ginunn-is1lG2iuni+ G22un2+G23un3+.+G2nunn=is11(3-3)Gniuni+ Gn2un2+ Gnun3+ *.+ Gnnunn=isnn式(3-3)中具有相同下标的电导Gl.G22.G33等是各结点的自电导,具有不同下标的电导G12G13等是各结点间的互电导而自导总是正的,互导总是负的。显.然,如果两个结点之间没有电导的支路而直接相连,则相应的互导为零。此外,在分析电路中遇到的特殊情况,将通过实例给予分析和说明。5.特殊问题在支路电流法,网孔电流法,回路电流法和结点电压法中遇到受空源时如何处理?(1)当电路中含有受控源时,先将受控电源视为独立电源列写方程,再将受控源的控制量用支路电流、网孔电流、回路电流、结点电压来表示后带入方程加以整理,其余情况将通过实列给予加以分析。三、典型例题例3一1如图3一1所示电路,试用支路电流法求各支路电流It,2,I3。解:(1)选定各支路电流的参考方向如图所示。32112Ii(2)结点数2、独立结点数:n—1=2—1=1个,45故只能列一个KCL方程:①—I1+I2+I3=0C(3)独立回路数:1=b-(n-1)=3-1=2;b以支路电流为变量按顺时针绕行方向列出网孔回路的KVL方程:图3—1例3-1图22
电路习题集 第三章 电阻电路的一般分析 22 (1)式(3-1)和(3-2)中有相同下标的电阻 R11,R22,R33 等是各网孔和各回路的自阻,有不 同下标的电阻 R12,R23,R31 等是各网孔和回路的互阻。 (2)自阻总是正的,互阻取正还是取负,则由相关的两个网孔电流和回路电流通过公共电阻 时两者的参考方向是否相同来决定,相同时取正,相反时取负。显然,若两个回路和网孔间 没有公共电阻,则相应的互阻为零. (3)方程右方的 uS11,uS22,.分别为网孔和回路 1,2.等中电压源的代数和,取和时,各 电压源的方向与网孔和回路电流的方向一致的电压源前应取“—”号,否则取“+”号。 4.结点电压法 结点电压法是以结点电压为未知量,应用 KCL 列出结点电流方程,然后用结点电压 来表示各支路电流代入结点电流方程。一个具有(n+1)个结点,b 条支路的电路当选定 任一结点为参考结点后,其余的 n 个结点是独立的,它的结点电压方程有: G11un1+ G12un1+ G13un3+ . + G1nunn=iS11 G21un1+ G22un2+ G23un3+ . + G2nunn=iS11 . Gn1un1+ Gn2un2+ Gn3un3+ . + Gnnunn=iSnn 式(3-3)中具有相同下标的电导 G11,G22,G33 等是各结点的自电导,具有不同下标的电导 G12,G13.等是各结点间的互电导而自导总是正的,互导总是负的。显.然,如果两个结点之 间没有电导的支路而直接相连,则相应的互导为零。此外,在分析电路中遇到的特殊情 况,将通过实例给予分析和说明。 5.特殊问题 在支路电流法,网孔电流法,回路电流法和结点电压法中遇到受空源时如何处理? (1)当电路中含有受控源时,先将受控电源视为独立电源列写方程,再将受控源的控制量 用支路电流、网孔电流、回路电流、结点电压来表示后带入方程加以整理.其余情况将通 过实列给予加以分析。 三、 典型例题 例 3-1 如图 3—1 所示电路,试用支路电流法求各支路电流 I1,I2,I3 。 解:(1)选定各支路电流的参考方向如图所示。 (2)结点数 2、独立结点数: n-1=2-1=1 个, 故只能列一个 KCL 方程: -I1+I2+I3=0 ① (3)独立回路数: l=b-(n-1)=3-1=2; 以支路电流为变量按顺时针绕行方向列出网孔 回路的 KVL 方程: 图 3—1 例 3-1 图 (3-3)
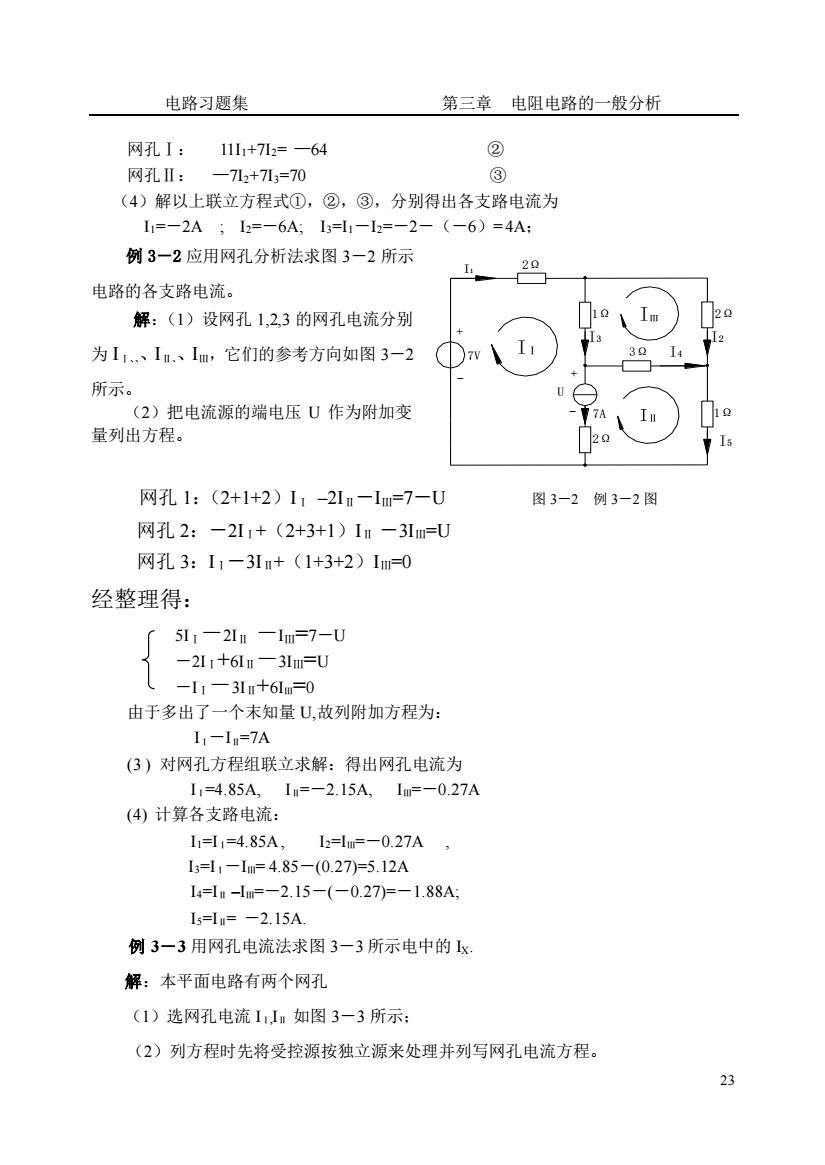
电路习题集第三章电阻电路的一般分析②网孔I:1111+712= —64?网孔IⅡ:—712+713=70(4)解以上联立方程式①,②,③,分别得出各支路电流为I=-2A :I2=-6A;I3=li-I2=-2—(-6)=4A;例3-2应用网孔分析法求图3-2所示20Ii电路的各支路电流。20解:(1)设网孔1,2,3的网孔电流分别30I4为I1.、In.、Im,它们的参考方向如图3一2所示。(2)把电流源的端电压U作为附加变7A量列出方程。Is网孔1:(2+1+2)11-21m—Im=7-U图3-2例3-2图网孔2:-2Ir+(2+3+1)Im—3Im=U网孔3:I—3I+(1+3+2)Im=0经整理得:51—21m—Im=7-U—21+61—31m=UI—3+61m=0由于多出了一个末知量U.故列附加方程为:I-I=7A(3)对网孔方程组联立求解:得出网孔电流为I,=4.85A,In=-2.15A,Im=-0.27A(4)计算各支路电流:Ii=I,=4.85A,I2=Im=—0.27AI3=I,-Im= 4.85—(0.27)=5.12AI4=Im-Im=—2.15—(—0.27)=—1.88A;Is=I= —2.15A例3一3用网孔电流法求图3一3所示电中的Ix解:本平面电路有两个网孔(1)选网孔电流II如图3-3所示;(2)列方程时先将受控源按独立源来处理并列写网孔电流方程。23
电路习题集 第三章 电阻电路的一般分析 23 网孔Ⅰ: 11I1+7I2= —64 ② 网孔Ⅱ: —7I2+7I3=70 ③ (4)解以上联立方程式①,②,③,分别得出各支路电流为 I1=-2A ; I2=-6A; I3=I1-I2=-2-(-6)= 4A; 例 3-2 应用网孔分析法求图 3-2 所示 电路的各支路电流。 解:(1)设网孔 1,2,3 的网孔电流分别 为 IⅠ、IⅡ、IⅢ,它们的参考方向如图 3-2 所示。 (2)把电流源的端电压 U 作为附加变 量列出方程。 网孔 1:(2+1+2)IⅠ –2IⅡ-IⅢ=7-U 图 3-2 例 3-2 图 网孔 2:-2IⅠ+(2+3+1)IⅡ -3IⅢ=U 网孔 3:IⅠ-3IⅡ+(1+3+2)IⅢ=0 经整理得: 5IⅠ-2IⅡ -IⅢ=7-U -2IⅠ+6IⅡ-3IⅢ=U -IⅠ-3IⅡ+6IⅢ=0 由于多出了一个末知量 U,故列附加方程为: IⅠ-IⅡ=7A (3 ) 对网孔方程组联立求解:得出网孔电流为 IⅠ=4.85A, IⅡ=-2.15A, IⅢ=-0.27A (4) 计算各支路电流: I1=IⅠ=4.85A, I2=IⅢ=-0.27A , I3=IⅠ-IⅢ= 4.85-(0.27)=5.12A I4=IⅡ –IⅢ=-2.15-(-0.27)=-1.88A; I5=IⅡ= -2.15A. 例 3-3 用网孔电流法求图 3-3 所示电中的 IX. 解:本平面电路有两个网孔 (1)选网孔电流 IⅠ,IⅡ 如图 3-3 所示; (2)列方程时先将受控源按独立源来处理并列写网孔电流方程。 + 7A 2Ω - - U I5 1Ω I3 1Ω + IⅠ 7V I1 2Ω 2Ω I2 3Ω I4 IⅢ
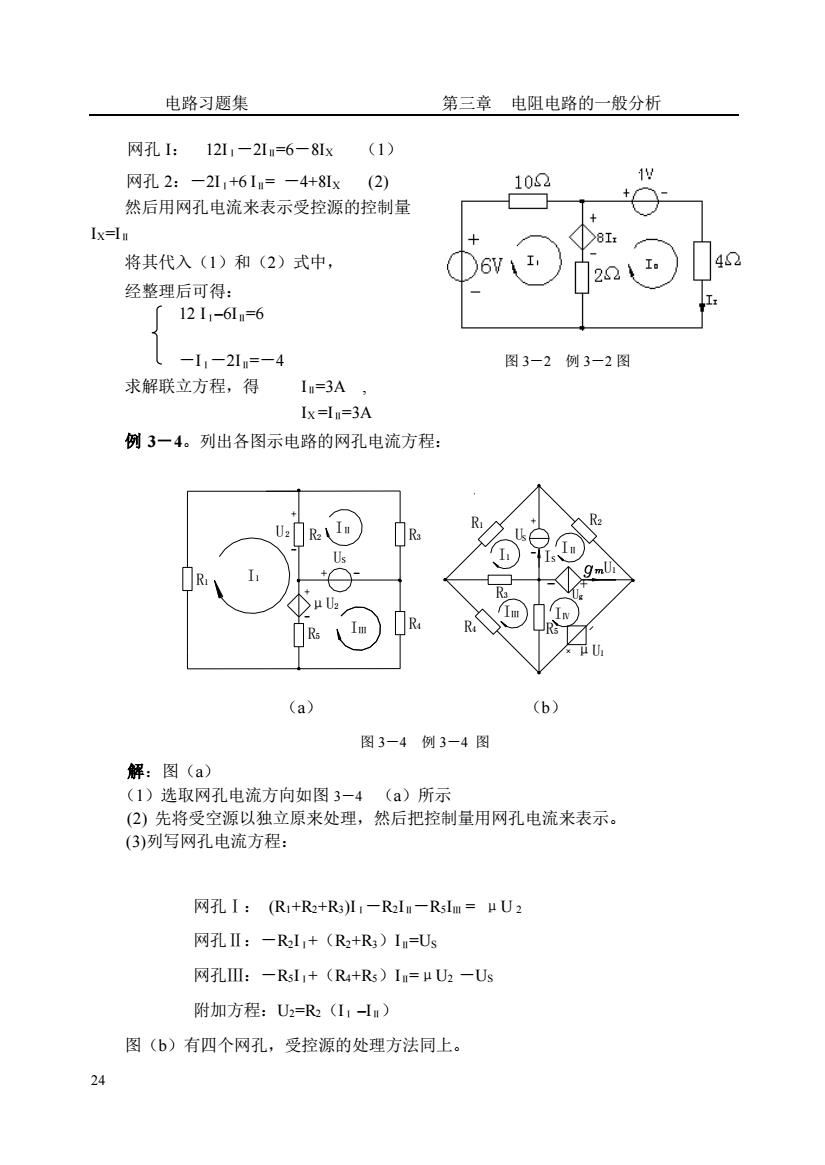
电路习题集第三章电阻电路的一般分析网孔I:(1)121,—21=6—8Ix1V102网孔2:—2I,+6I=—4+81x(2)然后用网孔电流来表示受控源的控制量Ix=I n4C将其代入(1)和(2)式中,经整理后可得:12 I,-61 =6-I,-21=-4图3-2例3-2图求解联立方程,得Is=3A,Ix=In=3A例3一4。列出各图示电路的网孔电流方程:RR(a)(b)图3-4例3-4图解:图(a)(1)选取网孔电流方向如图3一4(a)所示(2)先将受空源以独立原来处理,然后把控制量用网孔电流来表示。(3)列写网孔电流方程:网孔I:(R1+R2+R3)I-R2-Rslm=μU2网孔Il:—R21,+(R2+R)I=Us网孔IIl:-RsI+(R+Rs)I=μU-Us附加方程:U2=R2(I-Im)图(b)有四个网孔,受控源的处理方法同上。24
电路习题集 第三章 电阻电路的一般分析 24 网孔 I: 12IⅠ-2IⅡ=6-8IX (1) 网孔 2:-2IⅠ+6 IⅡ= -4+8IX (2) 然后用网孔电流来表示受控源的控制量 IX=IⅡ 将其代入(1)和(2)式中, 经整理后可得: 12 IⅠ–6IⅡ=6 -IⅠ-2IⅡ=-4 图 3-2 例 3-2 图 求解联立方程,得 IⅡ=3A , IX =IⅡ=3A 例 3-4。列出各图示电路的网孔电流方程: R1 I1 + - μU2 R5 - + IⅢ R4 U2 R2 - + US IⅡ R3 U1 R4 R3 IⅢ R5 + - μU1 Ug IⅣ - + R1 US I1 - + R2 IⅡ IS (a) (b) 图 3-4 例 3-4 图 解:图(a) (1)选取网孔电流方向如图 3-4 (a)所示 (2) 先将受空源以独立原来处理,然后把控制量用网孔电流来表示。 (3)列写网孔电流方程: 网孔Ⅰ: (R1+R2+R3)IⅠ-R2IⅡ-R5IⅢ = μU 2 网孔Ⅱ:-R2IⅠ+(R2+R3)IⅡ=US 网孔Ⅲ:-R5IⅠ+(R4+R5)IⅡ=μU2 -US 附加方程:U2=R2(IⅠ –IⅡ) 图(b)有四个网孔,受控源的处理方法同上
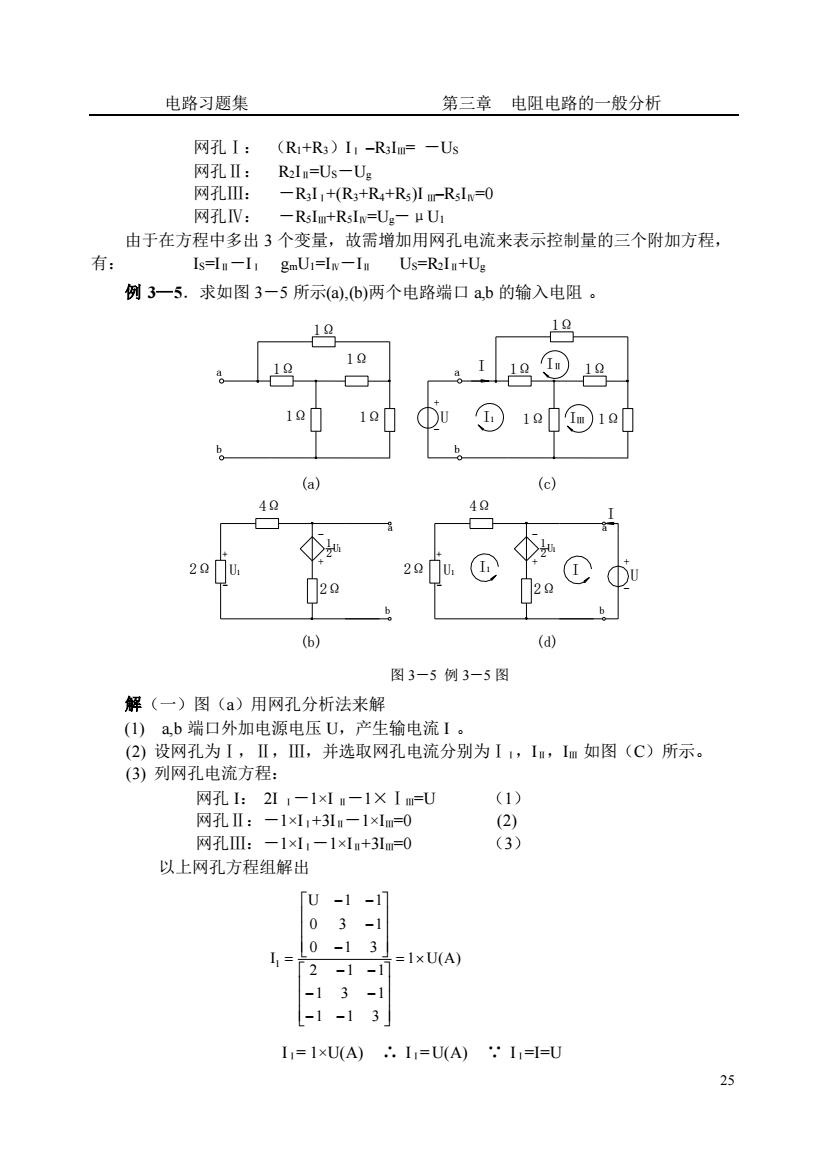
电路习题集第三章电阻电路的一般分析网孔I:(Ri+R3)I/-R3lm=—Us网孔IⅡI:R2ln=Us-Ug网孔III:—RI+(R3+R+Rs)Iμ-RsI=0网孔IV:-RsIm+RsI=U.-μUi由于在方程中多出3个变量,故需增加用网孔电流来表示控制量的三个附加方程,有:Is=In-I,Us=R2ln+UggmUi=Iv—In例3一5.求如图3一5所示(a),(b)两个电路端口a,b的输入电阻。19121010a1210O11QO60(a)(c)4040202029290(b)(d)图3-5例3-5图解(一)图(a)用网孔分析法来解(1)a,b端口外加电源电压U,产生输电流I。(2)设网孔为I,II,IⅢ,并选取网孔电流分别为I1,Iu,Im如图(C)所示。(3)列网孔电流方程:(1)网孔I:2-1XI-1×Im=U(2)网孔I:—1×I+3I—1×Im=0(3)网孔Ⅲl:—1×I,—1×I+3Im=0以上网孔方程组解出[U -1 -1]030-13=1xU(A)I =2-1-1-1 3 -11-13I,= 1xU(A):. I,=U(A):,=[=U25
电路习题集 第三章 电阻电路的一般分析 25 网孔Ⅰ: (R1+R3)IⅠ –R3IⅢ= -US 网孔Ⅱ: R2IⅡ=US-Ug 网孔Ⅲ: -R3IⅠ+(R3+R4+R5)I Ⅲ–R5IⅣ=0 网孔Ⅳ: -R5IⅢ+R5IⅣ=Ug-μU1 由于在方程中多出 3 个变量,故需增加用网孔电流来表示控制量的三个附加方程, 有: IS=IⅡ-IⅠ gmU1=IⅣ-IⅡ US=R2IⅡ+Ug 例 3—5.求如图 3-5 所示(a),(b)两个电路端口 a,b 的输入电阻 。 1Ω b a b a U + - I1 IⅡ IⅢ b a + - 2Ω U1 + - 1 2 U1 2Ω 2Ω 2Ω U1 - + + - 4Ω b a U 1 2 1 I1 I I - U + I 1Ω 1Ω 1Ω 1Ω 1Ω 1Ω 1Ω 1Ω 1Ω 4Ω (a) (c) (b) (d) 图 3-5 例 3-5 图 解(一)图(a)用网孔分析法来解 (1) a,b 端口外加电源电压 U,产生输电流 I 。 (2) 设网孔为Ⅰ,Ⅱ,Ⅲ,并选取网孔电流分别为ⅠⅠ,IⅡ,IⅢ 如图(C)所示。 (3) 列网孔电流方程: 网孔 I: 2I Ⅰ-1×I Ⅱ-1×ⅠⅢ=U (1) 网孔Ⅱ:-1×IⅠ+3IⅡ-1×IⅢ=0 (2) 网孔Ⅲ:-1×IⅠ-1×IⅡ+3IⅢ=0 (3) 以上网孔方程组解出 1 U(A) 1 1 3 1 3 1 2 1 1 0 1 3 0 3 1 U 1 1 I 1 = − − − − − − − − − − = IⅠ= 1×U(A) ∴ IⅠ= U(A) ∵ IⅠ=I=U