
电路习题集第九章含有耦合电感的电路第九章含有耦合电感的电路一基本要求1.掌握互感线圈中电压、电流的关系,了解互感系数、同名端的含义。2.会应用互感消去法(去耦法)分析计算含有互感的电路,这是本章的重点。3.熟悉空心变压器的原、副边等效电路。4.熟悉理想变压器的三个作用:变换电压、电流、阻抗。二.本章要点1.两互感的伏安关系(耦合电感又称互感)di+Mdi=[U,=joLi+jOMi,dtdt或MU,=joLjoMiun=Ladttdt电压、电流取关联参考方向时,同名端为同侧时,互感电压取“+”号,同名端为异侧时,互感电压取“_”号。2.同名端同名端又称对应端,电流分别从同名端流入时,所产生的互感磁通与自感磁通的方向一致(互相增强)。3.含互感电路的分析方法1>可将互感电压用一个电流控制电压源(CCVS)替代,然后用一般分析方法进行分析计算。M-2>互感消去法(去耦法)<1>互感串联业春两互感串联的等效电感为:L=+L±2M顺接时取“+”号,。。LM。反接时取“_”号。图9-1两互感串联电路《2>一般情况(具有公共节点)121'20Qi211+ I1i2去揭3L1+M3L2+M3L2.33行+i上面符号为同侧联接3 ±M下面符号为异侧联接O0 (0,3)图9-2互感消去等效电路75
电路习题集 第九章 含有耦合电感的电路 75 第九章 含有耦合电感的电路 一. 基本要求 1.掌握互感线圈中电压、电流的关系,了解互感系数、同名端的含义。 2.会应用互感消去法(去耦法)分析计算含有互感的电路,这是本章的重点。 3.熟悉空心变压器的原、副边等效电路。 4.熟悉理想变压器的三个作用:变换电压、电流、阻抗。 二.本章要点 1.两互感的伏安关系(耦合电感又称互感) = = dt di M dt di u L dt di M dt di u L 2 1 2 2 1 2 1 1 或 = = 2 2 2 1 1 1 1 2 j j j j U L I MI U L I MI 电压、电流取关联参考方向时,同名端为同侧时,互感电压取“+”号,同名端为异侧时, 互感电压取“-”号。 2.同名端 同名端又称对应端,电流分别从同名端流入时,所产生的互感磁通与自感磁通的方向一致 (互相增强)。 3.含互感电路的分析方法 1>可将互感电压用一个电流控制电压源(CCVS)替代,然后用一般分析方法进行分析计算。 2>互感消去法(去耦法) <1>互感串联 两互感串联的等效电感为: L = L1 + L2 2M 顺接时取“+”号, 反接时取“-”号。 图 9-1 两互感串联电路 <2>一般情况(具有公共节点) 图 9-2 互感消去等效电路
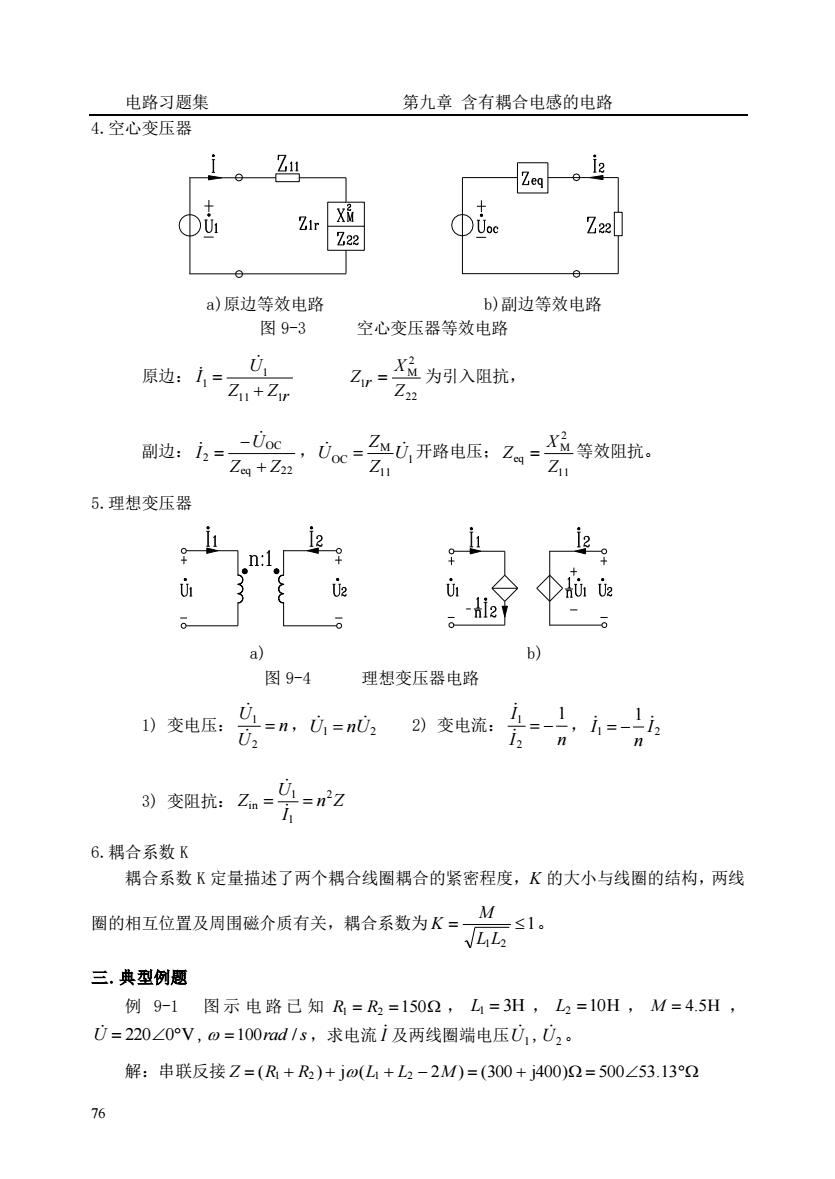
电路习题集第九章含有耦合电感的电路4.空心变压器Z11e+XXMZirZ22DUiDUooZ22a)原边等效电路b)副边等效电路图9-3空心变压器等效电路u,验为引入阻抗,原边:Z.Z.+ZrZ22X等效阻抗。UocZMU,开路电压;0.副边:LOCZi1Z1Zeq + Z225.理想变压器/Aiii20+0+n:1UU2uHurje-Hi21o100a)b)图9-4理想变压器电路U,i-1U,=nU,112)变电流:i=-1)变电压:En:U2i,nnU.=n?z3)变阻抗:Zin16.耦合系数K耦合系数K定量描述了两个耦合线圈耦合的紧密程度,K的大小与线圈的结构,两线M圈的相互位置及周围磁介质有关,耦合系数为K=≤1.VLL三,典型例题例9-1图示电路已知R=R2=150Q,L=3H,L=10H,M=4.5H,U=220Z0V,の=100rad/s,求电流i及两线圈端电压U,Uz。解:串联反接Z=(R+R2)+jo(L+Lz-2M)=(300+j400)2=500Z53.13°276
电路习题集 第九章 含有耦合电感的电路 76 4.空心变压器 a)原边等效电路 b)副边等效电路 图 9-3 空心变压器等效电路 原边: Z Z r U I 11 1 1 1 + = 22 2 M 1 Z X Z r = 为引入阻抗, 副边: eq 22 OC 2 Z Z U I + − = , 1 11 M OC U Z Z U = 开路电压; 11 2 M eq Z X Z = 等效阻抗。 5.理想变压器 a) b) 图 9-4 理想变压器电路 1) 变电压: n U U = 2 1 ,U1 nU2 = 2) 变电流: I n I 1 2 1 = − , 1 2 1 I n I = − 3) 变阻抗: n Z I U Z 2 1 1 in = = 6.耦合系数 K 耦合系数 K 定量描述了两个耦合线圈耦合的紧密程度, K 的大小与线圈的结构,两线 圈的相互位置及周围磁介质有关,耦合系数为 1 1 2 = L L M K 。 三.典型例题 例 9-1 图 示 电 路 已 知 R1 = R2 =150 , L1 = 3H , L2 =10H , M = 4.5H , U = 2200V, =100rad /s ,求电流 I 及两线圈端电压 U1 ,U2 。 解:串联反接 Z = (R1 + R2 ) + j(L1 + L2 − 2M ) = (300 + j400) = 50053.13

电路习题集第九章含有耦合电感的电路:i-0220Z0°=0.44Z-53.13°AZ500Z53.13°MRR两线圈端电压分别为福l*U2U,=(R +joL -joM)iTh0=(150+j300-j450)×0.44/-53.13g=93.3-98.1°VU,=(R, +joL,-joM)i图9-5例题9-1图=(150+j1000-j450)×0.44Z-53.13°=250.8Z21.65°V例9-2工频交流电源电压U=220V,两互感线圈串联,顺接时,电流为3A,功率为225W,反接时电流为8A。求两线圈的互感M。解:顺接时Z=(R+R)+jo(L+L+2M)反接时Z=(R+R2)+jo(L+L-2M)220zl=73.332顺接时:3P=PR,.R=R+R=-=250下320(L + Lz +2M)= /z- R2 =68.94Q68.94=0.22Hi+L2+2M=6?314反接时:[21-20=27.5080(L + L2 -2M)= /z-R2 =11.46QI+L -2M = 11.466=0.0365H②314互感M:M=(+L+2M)-(L+L-2M)_0.22-0.0365=0.0459H44例9-3图示电路,R=32,R2=52,0L=7.52,0L=12.5Q,0M=62,U=50Z0°V,分别求开关S打开和闭合时的电流i。解:1)S打开,两线圈为串联顺接Z=(R+R2)+ jo(L+L2+2M)=(8+j32)2U50Z0°i=1.52/-75.96°AZ8+j3277
电路习题集 第九章 含有耦合电感的电路 77 ∴ 0.44 53.13 A 500 53.13 220 0 = − = = Z U I 两线圈端电压分别为 U R L M I 1 = ( 1 + j 1 − j ) = (150 + j300 − j450)0.44−53.13 = 93.3 − 98.1V U R L M I 2 = ( 2 + j 2 − j ) 图 9-5 例题 9-1 图 = (150 + j1000 − j450)0.44−53.13 = 250.821.65V 例 9-2 工频交流电源电压 U = 220V ,两互感线圈串联,顺接时,电流为 3A ,功率 为 225W ,反接时电流为 8A 。求两线圈的互感 M 。 解:顺接时 Z = (R1 + R2 ) + j(L1 + L2 + 2M ) 反接时 Z = (R1 + R2 ) + j(L1 + L2 − 2M ) 顺接时: = = 73.33 3 220 Z P I R 2 = ,∴ = + = = = 25 3 225 2 2 1 2 I P R R R ( + + 2 ) = − = 68.94 2 2 L1 L2 M Z R 0.22H 314 68.94 L1 + L2 + 2M = = ① 反接时: = = 27.5 8 220 Z ( + − 2 ) = − =11.46 2 2 L1 L2 M Z R 0.0365H 314 11.46 L1 + L2 − 2M = = ② 互感 M : 0.0459H 4 0.22 0.0365 4 ( 1 2 2 ) ( 1 2 2 ) = − = + + − + − = L L M L L M M 例 9-3 图示电路, R1 = 3, R2 = 5 ,L1 = 7.5 ,L2 =12.5 ,M = 6 , U = 500V ,分别求开关 S 打开和闭合时的电流 I 。 解:1) S 打开,两线圈为串联顺接 Z = (R1 + R2 ) + j(L1 + L2 + 2M ) = (8 + j32) 1.52 75.96 A 8 32 50 0 = − + = = Z j U I
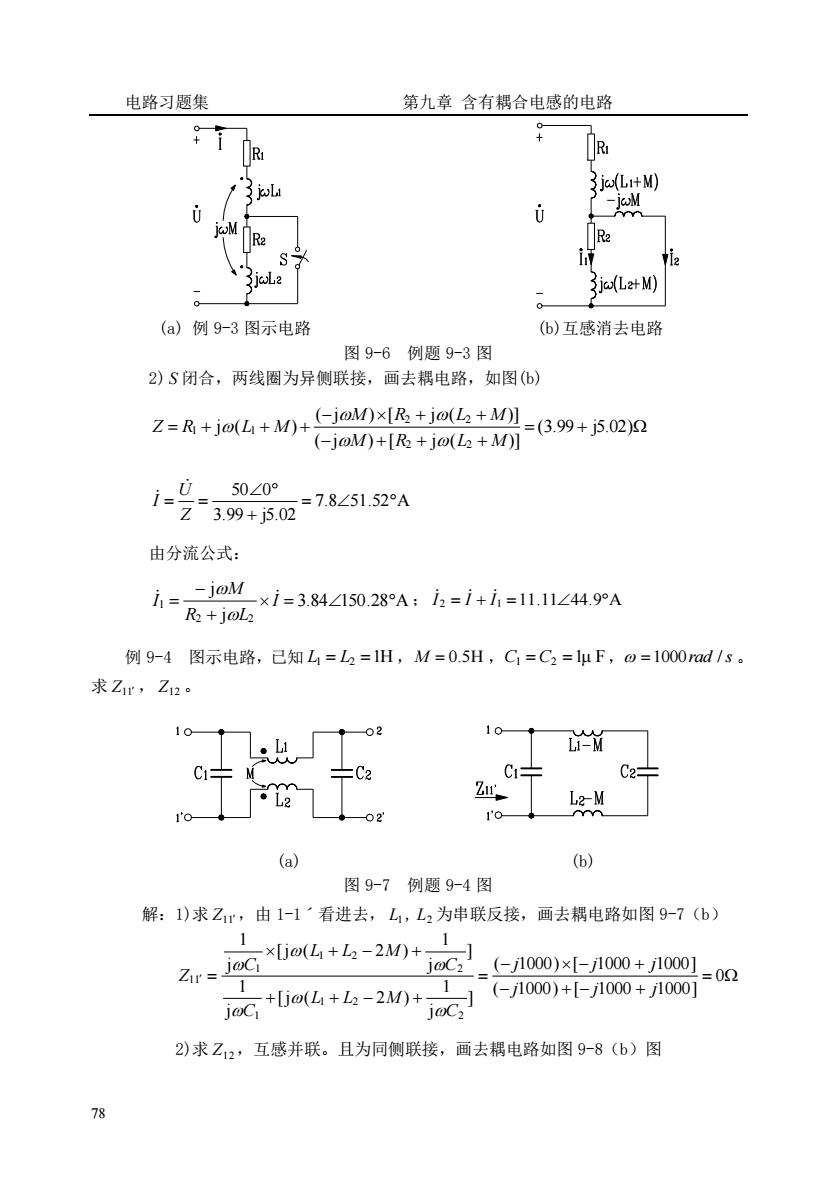
电路习题集第九章含有耦合电感的电路o+Ri3 ja(LI+M)jwLa-joMi二GMR2R2i2S-3jwL23 jo(L2+ M)(a)例9-3图示电路(b)互感消去电路图9-6例题9-3图2)S闭合,两线圈为异侧联接,画去耦电路,如图(b)Z=R +jo(L4 +M)+(-joM)x[R +jo(L +M)](3.99+ j5.02)2(-joM)+[R2 + jo(L +M)]u50Z0°i7.8/51.52°AZ3.99 + j5.02由分流公式:-joMxi=3.84Z150.28°A:iz=i+i,=11.11Z44.9°Ai=R2+ joLl2例9-4图示电路,已知L=L=1H,M=0.5H,C=C=luF,の=1000rad/s。求Zr,Z12。10021CLI-M.LiCi=C2-C1C2TZrL2-M21oYY1'002(b)(a)图9-7例题9-4图解:1)求Zur,由1-1看进去,L,L,为串联反接,画去耦电路如图9-7(b)1x[jo(L +L,-2M)+j1000)×[-j1000+j10001joCijoC2Zur091-(-j1000)+[-j1000+j1000]+[jo(L+L2-2M)+joCij0C22)求Z12,互感并联。且为同侧联接,画去耦电路如图9-8(b)图78
电路习题集 第九章 含有耦合电感的电路 78 (a) 例 9-3 图示电路 (b)互感消去电路 图 9-6 例题 9-3 图 2) S 闭合,两线圈为异侧联接,画去耦电路,如图(b) = + − + + + − + + = + + + (3.99 j5.02) ( j ) [ j ( )] ( j ) [ j ( )] j ( ) 2 2 2 2 1 1 M R L M M R L M Z R L M 7.8 51.52 A 3.99 j5.02 50 0 = + = = Z U I 由分流公式: 3.84 150.28 A j j 2 2 1 = + − = I R L M I ; I 2 = I + I 1 =11.1144.9A 例 9-4 图示电路,已知 L1 = L2 =1H ,M = 0.5H ,C1 =C2 =1μ F, =1000rad /s 。 求 Z11 , Z12 。 (a) (b) 图 9-7 例题 9-4 图 解:1)求 Z11 ,由 1-1ˊ看进去, L1 , L2 为串联反接,画去耦电路如图 9-7(b) = − + − + − − + = + + − + + − + = 0 ( 1000) [ 1000 1000] ( 1000) [ 1000 1000] ] j 1 [j ( 2 ) j 1 ] j 1 [j ( 2 ) j 1 2 1 2 1 2 1 2 1 11 j j j j j j C L L M C C L L M C Z 2)求 Z12 ,互感并联。且为同侧联接,画去耦电路如图 9-8(b)图
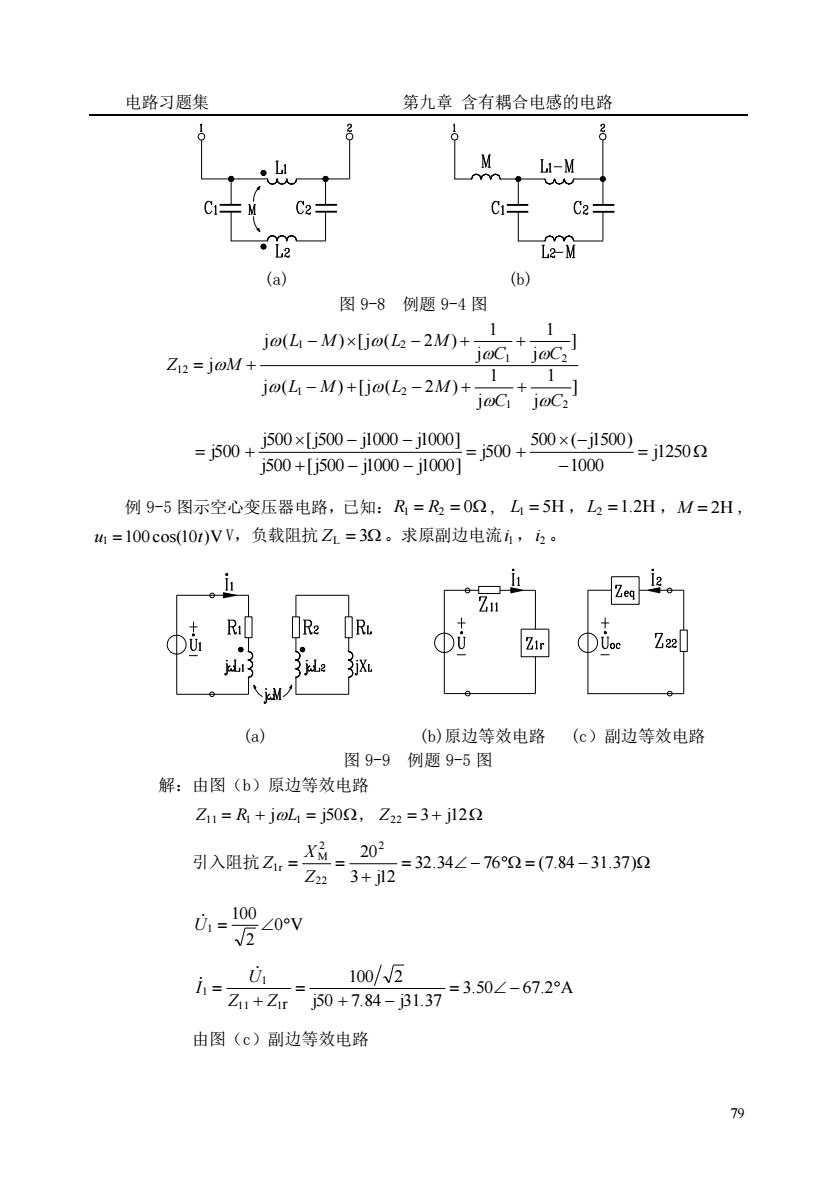
电路习题集第九章含有耦合电感的电路20-02O0MLi-MLiYC2C2CiL2-ML2(a)(b)图9-8例题9-4图1jo(L-M)x[jo(L-2M)+jacjaC2Z12 = joM +1jo(L -M)+[jo(L, -2M)+jaCijaC2j500×[j500j1000-j1000]500 ×(-j1500)=j500+j500+j125021000j500+[j500-j1000-j1000]例9-5图示空心变压器电路,已知:R=Rz=0Q,L=5H,L=1.2H,M=2H,ui=100cos(10t)VV,负载阻抗ZL=3Q。求原副边电流i,i2。iiZ11++RiR2RLZ22PZirDUocOUjLijXr(a)(b)原边等效电路(c)副边等效电路图9-9例题9-5图解:由图(b)原边等效电路Z11=R + j@L=j50Q2,Z22=3+j12Q202XM引入阻抗Z=32.34/-76°=(7.84-31.37)2Z223+j12U,=100ZO0VV20,100//2ii:Jj50 +7.84-j31.37 =3.50Z -67.2°AZut + Zir由图(c)副边等效电路79
电路习题集 第九章 含有耦合电感的电路 79 (a) (b) 图 9-8 例题 9-4 图 ] j 1 j 1 j ( ) [j ( 2 ) ] j 1 j 1 j ( ) [j ( 2 ) j 1 2 1 2 1 2 1 2 12 C C L M L M C C L M L M Z M − + − + + − − + + = + = − − = + + − − − − = + j1250 1000 500 ( j1500) j500 j500 [j500 j1000 j1000] j500 [j500 j1000 j1000] j500 例 9-5 图示空心变压器电路,已知: R1 = R2 = 0 , L1 = 5H ,L2 =1.2H ,M = 2H , u1 =100 cos(10t)V V,负载阻抗 ZL = 3 。求原副边电流 i1 ,i2 。 (a) (b)原边等效电路 (c)副边等效电路 图 9-9 例题 9-5 图 解:由图(b)原边等效电路 Z11 = R1 + jL1 = j50, Z22 = 3 + j12 引入阻抗 = − = − + = = 32.34 76 (7.84 31.37) 3 j12 202 22 2 M 1r Z X Z 0 V 2 100 U1 = 3.50 67.2 A j50 7.84 j31.37 100 2 11 1r 1 1 = − + − = + = Z Z U I 由图(c)副边等效电路