一、正态总体的抽样分布定理 当总体为正态分布时,教材上给出了4个重要的抽样分布定理 定理1一一样本均值、方差的分布R.141Th6.1) 设X1,X2,…,Xn是 取自正态总体N(μ,o2)的样本,则 ⑩X~N(4,): 正态分布的线性组合仍服从正态分布(P115例18) E=μ,DR=o2n(样本矩性质1P184Th1) 2) a5-玄K-xrs2 i=1 (3)X和S2相互独立. (2)与(3)证明参见参考文献 n=16 0.4 1=6 0.2 7 0 0 5 10 15 0 10 20
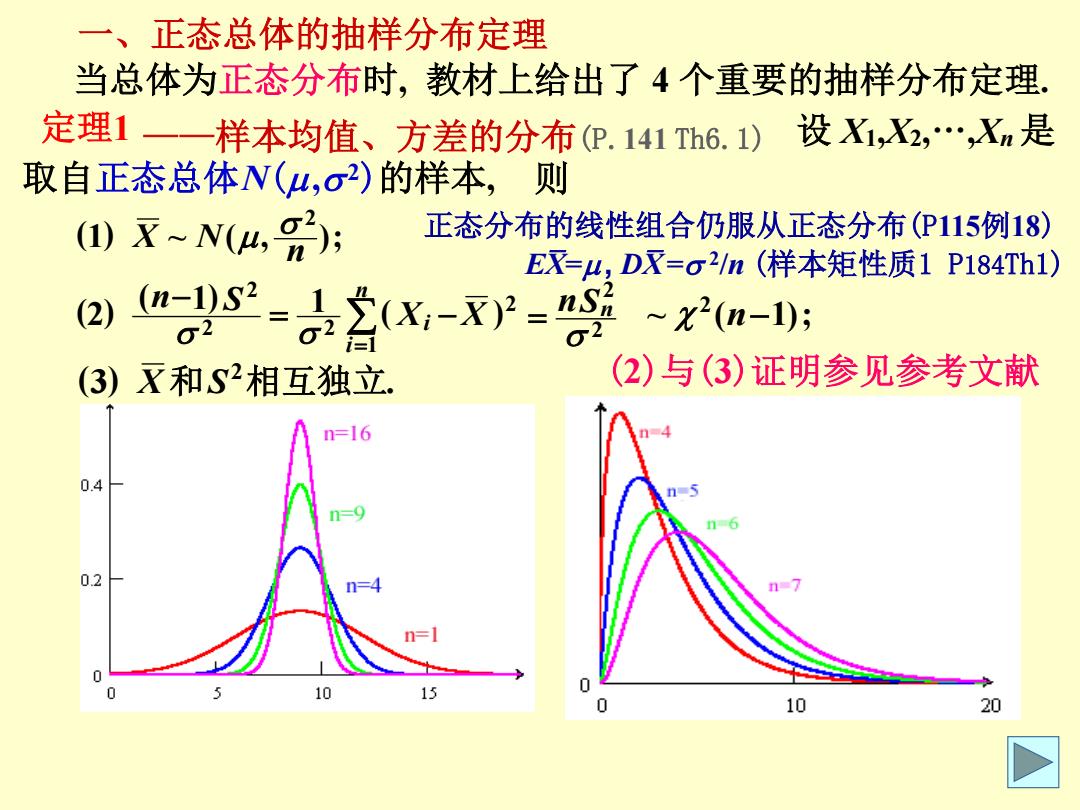
设 X1,X2,„,Xn 是 取自正态总体N(,2)的样本, 当总体为正态分布时, 教材上给出了 4 个重要的抽样分布定理. 一、正态总体的抽样分布定理 定理1 则 (1) ~ ( , ); 2 n X N n i Xi X n S 1 2 2 2 2 ( ) ( 1) 1 (2) (3) . X 和S 2相互独立 EX= , DX= 2 /n (样本矩性质1 P184Th1) 正态分布的线性组合仍服从正态分布(P115例18) 2 2 nSn ~ ( 1); 2 n (2)与(3)证明参见参考文献 ——样本均值、方差的分布(P.141 Th6.1)

定理2一一样本均值和方差标准化的抽样分布(P.142T) 设X1,X2,,X是取自正态总体N(山,σ2)的样本,则 X-4 X-4 ~t(n-1) Sn/An-1 证由定理t1的()知X~N(4,), → -业 ~N(0,1) on 由定理1的(3)与(2)知 :与 (n-1)S2 02 相互独立,且 X-4 由T分布定义知 X-4 Gn ~t(n-1). g2 上述两个定理中所涉及到的样本均是来自同一个正态总体, 但实际中,我们还经常需要考察来自不同的正态总体样本.不妨假 定取自不同总体的样本总是独立的
不妨假 定取自不同总体的样本总是独立的. 但实际中, 我们还经常需要考察来自不同的正态总体样本. 设 X1, X2, „, Xn 是取自正态总体 N(,2)的样本, 则 ~ ( 1) 1 t n S n X n 定理2——样本均值和方差标准化的抽样分布(P.142 Th) S n X n i Xi X 1 2 ( ) 证 由定理1的(1)知 ~ ( , ), 2 n X N ~ N(0,1), n X 由定理1的(3)与(2)知 n X 2 2 ( 1) 与 n S 相互独立, 且 ~ ( 1), ( 1) 2 2 2 n n S 由 T 分布定义知 ~ ( 1) . 2 2 t n S n X S n X 上述两个定理中所涉及到的样本均是来自同一个正态总体

定理3一一 两个正态总体的抽样分布(P.142Th) 设X,,,Xm是取自正态总体N(山☑的样本,Y,2,,Yn 是取自正态总体N(h☑的样本,则 卫-(山= (X-) ≈N0,1); 独立正态分布 D(X-) 的连续函数 (2) ~F(m,; 3) S/σ ~F(m-1,n-1), 含(出-4Pnci 其中Sx2,S,2分别是这两个样本的样本方差 证(2) -41~N0,1),由x2分布的定义知。(X-4x(m: O1 同 ,房(-一m:相互独立,由F分布的定义知 证(3) S/o1_(m-1))S/o(m-1) (n-1)So(n-1) 由F分布定义知(3)成立. (m-1)S_ 含(xm-: 1 同理, n-可S-x2n-0;
Y1, Y2, „, Yn 是取自正态总体 N(2 ,2 2)的样本, 相互独立, (3) 2 ~ ( 1, 1), 2 2 2 1 2 F m n S S Y X 则 定理3 —— 两个正态总体的抽样分布(P.142 Th) 其中 SX 2 , SY 2分别是这两个样本的样本方差 . 设 X1, X2, „, Xm 是取自正态总体 N(1 ,1 2)的样本, ~ ( , ); ( ) ( ) (2) 2 2 1 2 2 2 1 1 2 1 F m n Y n X m n i i m i i E(X Y ) 独立正态分布 D(X Y ) 的连续函数 证(2) 由 ~ (0,1) , 2 分布的定义知 1 1 N Xi 同理, ( ) ~ ( ); 1 2 2 1 2 1 1 X m m i i 证(3) , ( 1) ( 1) ( 1) ( 1) 2 2 2 2 1 2 2 2 2 2 1 2 n S n m S m S S Y X Y X m i i X X X m S 1 2 2 1 2 1 2 ( ) ( 1) 1 同理, ~ ( 1); ( 1) 2 2 2 2 n n SY ( ) ~ ( ); 1 2 2 1 2 2 2 Y n n i i ~ ( 1); 2 m Th1(2) 由F 分布定义知(3)成立. ~ (0, 1); ( ) (1) 2 2 2 1 1 2 N m n X Y 由F 分布的定义知

定理4一一两同方差正态总体的抽样分布(P.142Th) 设X,X,,Xm是取自正态总体N(山,o2)的样本,Y1,Y2,,Yn 是取自正态总体N(山,σ2)的样本,则有 吴了h二华-m+n-2),(S。=V (m-1)S录+(n-1)S2 m+n-2 m+n 定理6.1的特例 (2) 其中Sx2,S2分别是这两个样本的样本方差 证(1)由两异方差总体的抽样定理之(1): -T-(山-2)~N0,1); m足-xm-1,a超-x-:品+4 2 且相互独立,由x2分布的可加性知m-S主r-S-xm+m-2); 由t分布的定义知 X-7-(41-2) ~t(m+n-2), m-1)S+(n-1)S2 1 m+n-2 \m+n
定理4 Y1, Y2, „, Yn 是取自正态总体 N(2 ,2)的样本, ~ ( 2) , 1 1 ( ) (1) 1 2 t m n m n S X Y 其中SX 2 , SY 2分别是这两个样本的样本方差. 则有 —— 两同方差正态总体的抽样分布(P.142 Th) 证(1) 设 X1, X2, „, Xm 是取自正态总体 N(1 ,2)的样本, ) ; 2 ( 1) ( 1) ( 2 2 m n m S n S S X Y 2 ~ ( 1, 1) . 2 F m n S S Y X (2) 定理6.1的特例 由两异方差总体的抽样定理之(1): ~ (0, 1); 1 1 ( 1 2 ) N m n X Y ~ ( 1), ( 1) 2 2 2 m m SX ~ ( 1); ( 1) 2 2 2 n n SY 且相互独立, 由 2 分布的可加性知 ~ ( 2); ( 1) ( 1) 2 2 2 2 m n m SX n SY 由 t 分布的定义知 ~ ( 2) , 1 1 2 ( 1) ( 1) ( ) 2 2 1 2 t m n m n m n m S n S X Y X Y