
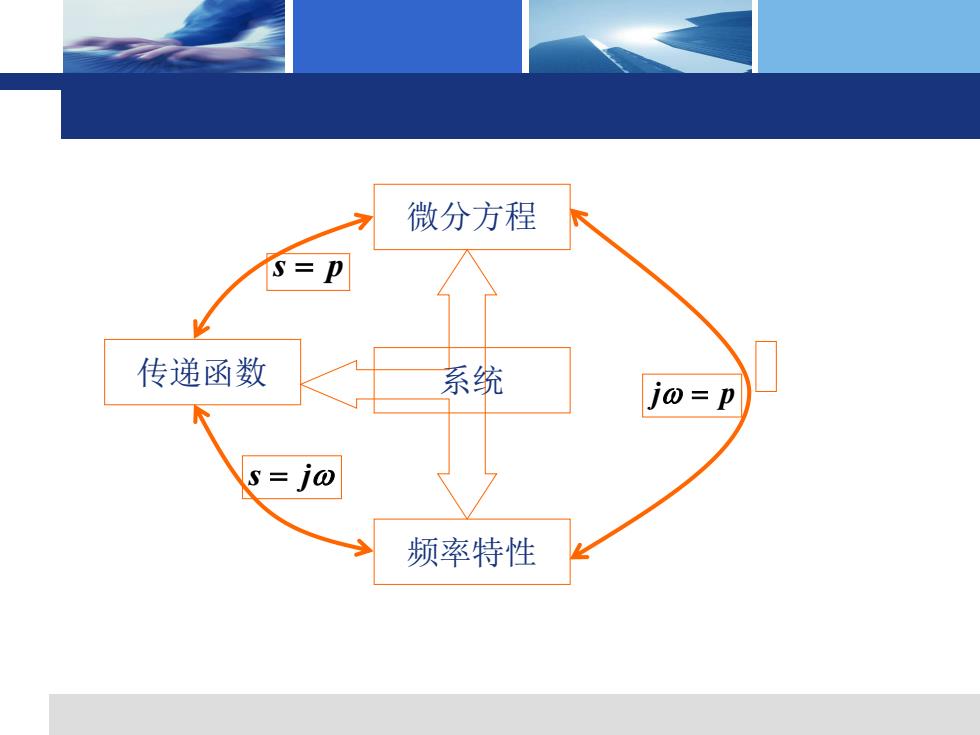
说明: 1.在稳态求出的输出信号与输入信号的幅值比是ω的非 线性函数,称为幅频特性YX=GGo)川 2.输出信号与输入信号的相位差是o的非线性函数,称 为相频特性它描述在稳态情况下,当系统输入不同频率 的谐波信号时,其相位产生超前(中>0)或滞后(中<0)的 特性, 3.幅频特性和相频特性总称为频率特性,记为 G(j@)=G(j@)ei-GiO) 4.频率特性的求取G(o)=G(s)s=j0 结论:频率特性和传递函数以及微分方程一样,也 表征了系统的运动规律,这就是频率响应能 够从频率特性出发研究系统的理论依据
, : , 4. G(j ) G(s) G(j ) G(j ) e 3. , . , ( 0) ( 0) . , 2. , , Y/X | G(j )| 1. : s j j G(j ) 够从频率特性出发研究系统的理论依据。 表征了系统的运动规律 这就是频率响应能 结论 频率特性和传递函数以及微分方程一样 也 频率特性的求取 幅频特性和相频特性总称为频率特性 记为 特性 的谐波信号时 其相位产生超前 或滞后 的 为相频特性它描述在稳态情况下 当系统输入不同频率 输出信号与输入信号的相位差 是 的非线性函数 称 线性函数 称为幅频特性 在稳态求出的输出信号与输入信号的幅值比是 的非 说明 = = = =
微分方程 S=卫 传递函数 系统 jo=p s=jo 频率特性
微分方程 频率特性 传递函数 系统 j = p s = j s = p

1. 幅相频率特性(Nyquist图) 当频率o从0到无穷大变化时,向量GGo)的端点在复 平面上的运动轨迹。 规定极坐标图的实轴正方向为相角零度线,逆时针转过 的角度为正,顺时针转过的角度为负。 2.对数频率特性(Bode图) 由两张图组成:一张是对数幅频特性,另一张是对数相频 特性
二. 频率特性的几何表示 1. 幅相频率特性(Nyquist 图) 当频率 从0到无穷大变化 时,向量G(j )的端点在复 平面上的运动轨迹。 规定极坐标图的实轴正方向为相角零度线,逆时针转过 的角度为正,顺时针转过的角度为负。 2. 对数频率特性(Bode图) 由两张图组成:一张是对数幅频特性,另一张是对数相频 特性

0 0=0 0→00 -45° u 0.707 0=1/T
RC网络的幅相曲线绘在s平面上 jv 0 u =0 →∞ -45° 0.707 =1/T

频率响应的Nyquist图 一.典型环节的Nyquist图 1.放大环节 频率特性( G(jo)=K 幅频特性A(o)=G(Uo)=K K 0 u 相频特性 (o)=∠G(Uo)=09
频率响应的Nyquist 图 一. 典型环节的Nyquist图 1. 放大环节 0 u jv K 频率特性 G(j) = K 幅频特性 A() = G(j) = K 相频特性 ( ) ( ) o = G j = 0