
说明: 1.网络的稳态输出仍是弦电压其频率与输入电压相同 幅值是输入电压的yr。(幅频特性,相角比输入电压 滞后-arctgT@(相频特性). V1+T2@2 它描述了网络在正弦输作用下,稳态输出时电压幅值 和相角随正弦输入电题率0变化的规律称为网络的频 率特性 3. I+ioT TS+1 S-jo
TS 1 S j 1 1 j T 1 1 j T 1 j 1 jT -jarctg T 1 1 T 1 1 1 3. . , , 2. e e - arctgT ( ). ( ), 1. , , : (1 jT ) 1 2 2 2 2 + + = + + + + = = = + 率特性 和相角随正弦输入电压频 率 变化的规律 称为网络的 频 它描述了网络在正弦输入作用下 稳态输出时电压幅值 滞 后 相频特性 幅值是输入电压的 幅频特性 相角比输入电压 网络的稳态输出仍是正弦电压 其频率与输入电压相同 说 明 T
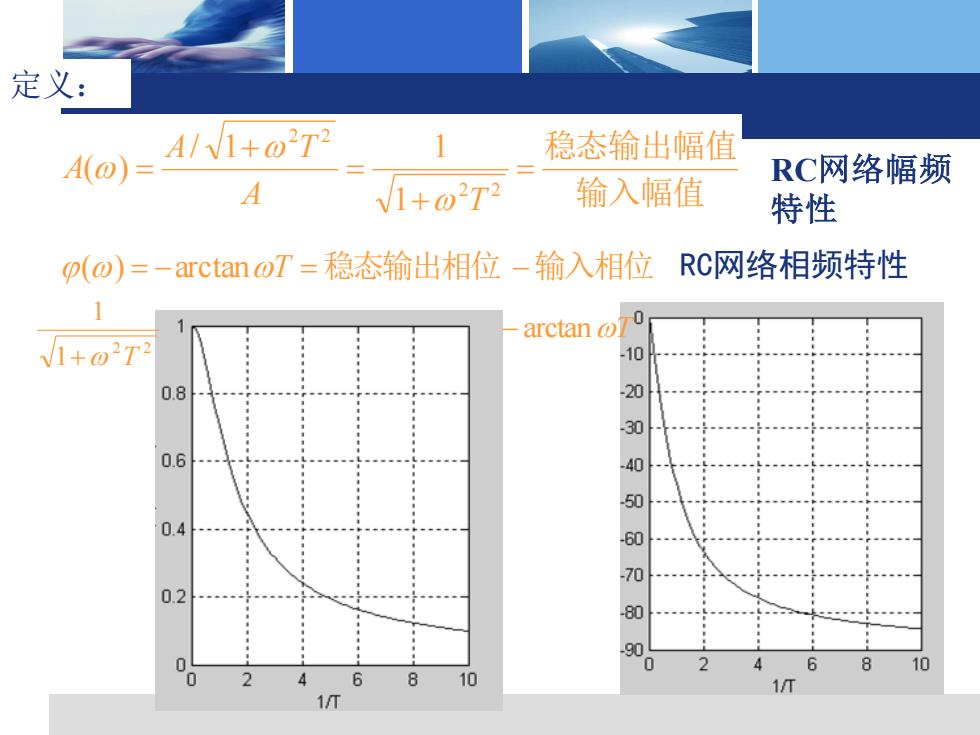
定义: A(o)= A/V1+02T2 稳态输出幅值 RC网络幅频 A V1+02T2 输入幅值 特性 p(o)=-arctan@T=稳态输出相位-输入相位 RC网络相频特性 1 arctan of 1+02T2 -10 0.8 20 0.6 0.4 040000 0.2 0 8 10 0 6 8 10 1/
定义: 输入幅值 稳态输出幅值 = + = + = 2 2 2 2 1 / 1 1 ( ) A T A T A RC网络幅频 特性 () = −arctan T = 稳态输出相位 −输入相位 RC网络相频特性 2 2 1 1 + T − arctan T

G(j0)= RCjo+11+jol 1 e/(-arctanoT) V1+02T2 A(@)ej) C电路的这一特性,对于任何稳定的线性网络都成立 虽然在前面的分析中,设定输入信号是正弦信号,然而频 率特性是系统的固有特性,与输入信号无关, 即当输入为非正弦信号时,系统仍然具有自身的频率特性
将s以j 代入RC网络传递函数,即得RC网络频率特性 RCj j T G j + = + = 1 1 1 1 ( ) ( arctan ) 2 2 1 1 j T e T − + = ( ) ( ) j = A e RC电路的这一特性,对于任何稳定的线性网络都成立 虽然在前面的分析中,设定输入信号是正弦信号,然而频 率特性是系统的固有特性,与输入信号无关, 即当输入为非正弦信号时,系统仍然具有自身的频率特性

频率特性定义为输出量的Fourier?变换与输入量 的Fourier?变换之比,即 G(w)-X.(o) X(io)
频率特性定义为输出量的Fourier变换与输入量 的Fourier变换之比,即 ( ) ( ) ( ) X j X j G j i 0 =

频率特性是一个复数,有三种表示: V(@) Gj) 代数式GUo)=U(o)+j(o) A(@) (@) 极坐标式 U()u G(Uo)=G(jo)∠G(jo)=Ao)∠p(o) 指数式 G(j@)=G(j@)ej2G()=A(@)e) A@)=G(j@)=JUP(@)+V2(@ U(@)=A@)cosp(@) V(o (@)=arctan V(@)=A(o)sino(@)
频率特性是一个复数,有三种表示: 代数式 G(j) =U() + jV() 极坐标式 ( ) ( ) ( ) ( ) ( ) j G j j G j = G j e = A e G( j) = G( j)G( j) = A()() 指数式 () ( ) () () 2 2 A = G j = U +V ( ) ( ) ( ) = U V arctan U() = A()cos() V() = A()sin() U() V() A() G(j) () u jv 0 频率特性的矢量图