
14.2 Redundant number representations 96 A symmetric signed-digit representation uses the digit set Dr.=a1,0,1,..a}where r is the radix and a is the largest digit in the set. A number in this representation is written as W- Xe=xr-1xw-3Xw-3…xn=∑xw-广 i=0 The sign of the number is given by the sign of the most significant non-zero digit. ·Digit set D<2.1>={1,0,1, ■3<2.1>=00110r0101 6
6 14.2 Redundant number representations A symmetric signed-digit representation uses the digit set D<r.α>={α, …, 1, 0, 1, …, α }, where r is the radix and α is the largest digit in the set. A number in this representation is written as : The sign of the number is given by the sign of the most significant non-zero digit. Digit set D<2.1>={1,0,1}, 3<2.1>=0011 or 0101 1 0 , 1 2 3 0 1 . .... W i i r W W W W i X x x x x x r

14.2 Redundant number representations /966 Minimally redundant and maximally redundant Digit Set D.r.d 0 Redundancy Factor p r-1 Incomplete <(r-1)/2 〈克 Complete but non-redundant =(r-1)/2 :含 Redundant ≥「r/2] >是 Minimally redundant =「r/2 and <1 Maximally redundant =r-1 =1 Over-redundant >r-1 >1 The greater the redundancy factor,the greater the redundancy of the representation. D2.1>is also referred to as signed binary digit (SBD), redundant signed digit(RSD),and borrow save(BS) representations. 7
7 Minimally redundant and maximally redundant The greater the redundancy factor, the greater the redundancy of the representation. D<2.1> is also referred to as signed binary digit (SBD), redundant signed digit (RSD), and borrow save (BS) representations. r 1 14.2 Redundant number representations

14.3 Carry-free Radix-2 Addition and /96 subtraction Redundant number representations limit the carry propagation to a few bit-positions,which is usually independent of the word length W. The algorithm to carry out signed binary digit addition is not unique,and therefore its logic implementation can be diverse. A radix-2 signed digit number is coded using 2 unsigned binary numbers,1 positive and 1 negative,as X=X+-X-. 8
8 14.3 Carry-free Radix-2 Addition and subtraction Redundant number representations limit the carry propagation to a few bit-positions, which is usually independent of the word length W. The algorithm to carry out signed binary digit addition is not unique, and therefore its logic implementation can be diverse. A radix-2 signed digit number is coded using 2 unsigned binary numbers, 1 positive and 1 negative, as X=X+-X -

14.3 Carry-free Radix-2 Addition and /96 subtraction In a hybrid operation,1st input operand and the output operand are in redundant signed digit representation,and the 2nd input operand is conventional unsigned number. A signed digit addition can be viewed as a concatenation of one hybrid addition and one hybrid subtraction. 9
9 In a hybrid operation, 1st input operand and the output operand are in redundant signed digit representation, and the 2nd input operand is conventional unsigned number. A signed digit addition can be viewed as a concatenation of one hybrid addition and one hybrid subtraction. 14.3 Carry-free Radix-2 Addition and subtraction
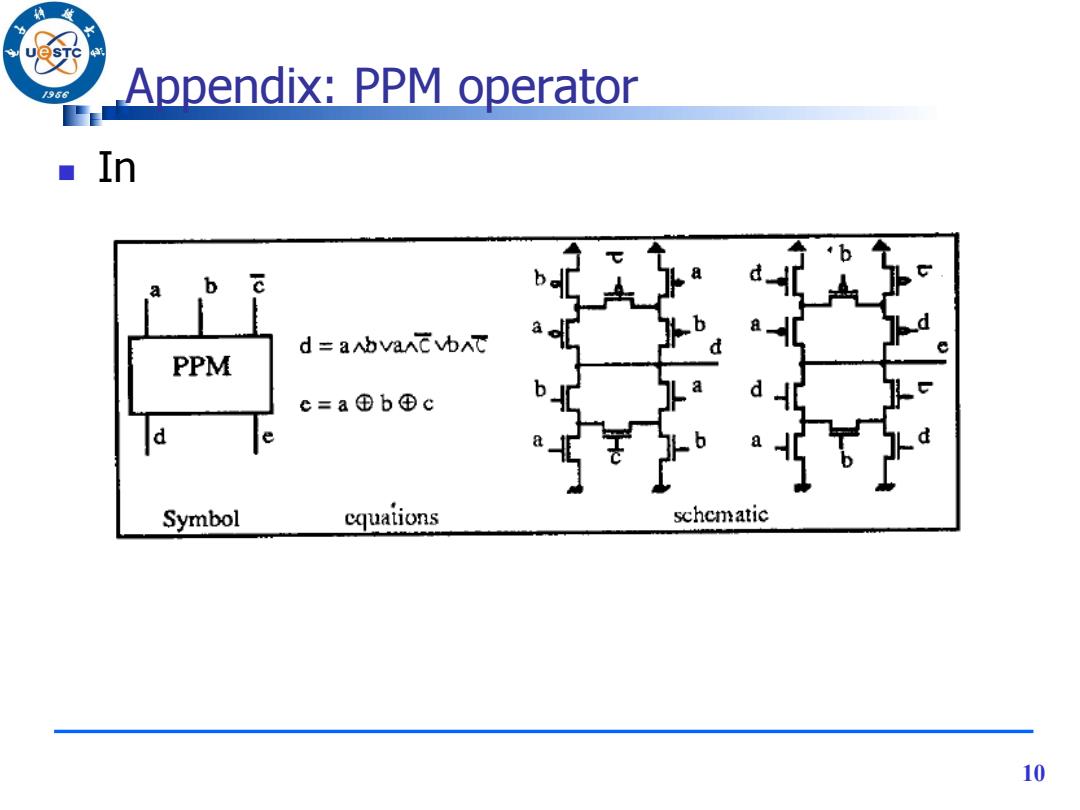
/966 Appendix:PPM operator In b b d=anbvancvbac PPM c=a⊕b⊕c d Symbol cquations schematic 10
10 In Appendix: PPM operator