第14章线性动态电路的复频域分析 本章目录 14.1 拉普拉斯变换的定义 14.2 拉普拉斯变换的基本性质 14.3 拉普拉斯反变换的部分分式展开 14.4 运算电路 14.5 用拉普拉斯变换法分析线性电路 14.6 网络函数的定义 14.7 网络函数的极点和零点 14.8 极点、零点与冲激响应 14.9 极点、零点与频率响应 1

重点 ①KL、元件VCR的运算形式,运算电路; ②运算法的求解步骤; ③网络函数的定义与类型、极点与零点的概念。 了难点 ①正确理解和计算动态元件初始值引起的附加电源; ②网络函数的零、极点与冲激响应和频率响应的关系。 与其它章节的联系 拉氏变换:解决电路的动态分析问题。即解决第7 章的问题,称之为运算法。是后续各章的基础,是前几 章基于变换思想的延续。网络函数部分以拉氏变换为基 础;冲激响应参见第7章、频率响应参见第11章
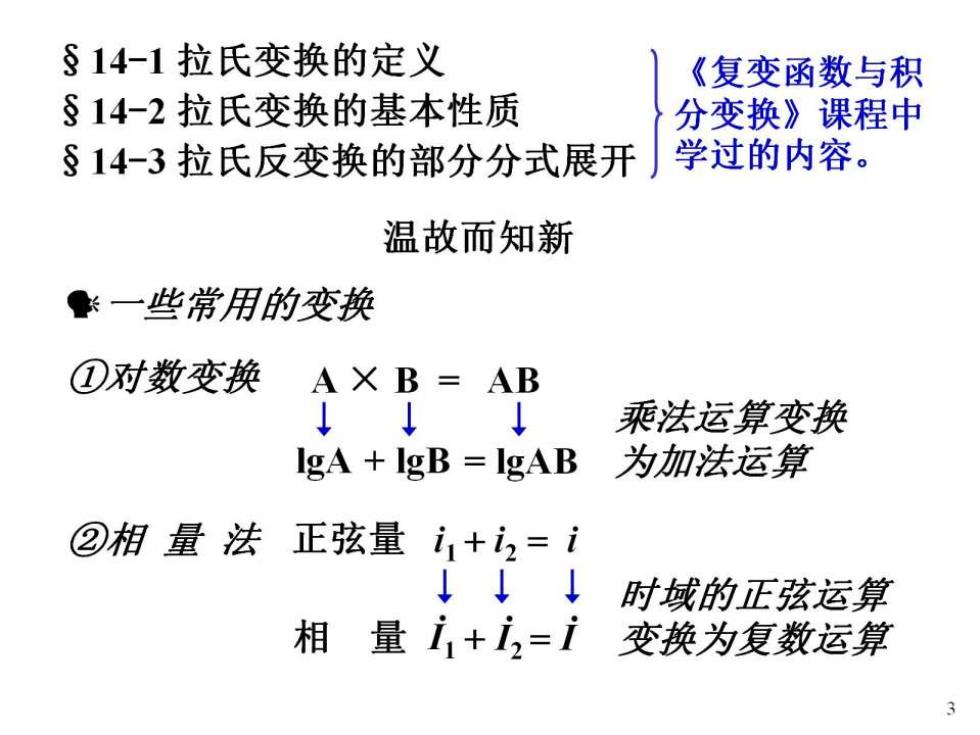
§14-1拉氏变换的定义 《复变函数与积 §14-2拉氏变换的基本性质 分变换》课程中 §14-3拉氏反变换的部分分式展开 学过的内容。 温故而知新 一些常用的变换 ①对数变换 AX B=AB ↓↓↓ 乘法运算变换 IgA IgB IgAB 为加法运算 ②相量法」 正弦量i1+i2=i ↓↓↓ 时域的正弦运算 相 量i+i2=i 变换为复数运算

引言 第七章研究了一阶电路和二阶电路,应用电路定律 和VCR建立方程,方程为以时间为自变量的线性常 微分方程,求解方程可得到时域内的解(经典法)。 对具有多个动态元件的复杂电路,建立时域的高阶 微分方程方程,直接求解方程工作量很大。 积分变换法:通过积分变换把时域函数变为频域函 数,从而把时间域的高阶微分方程变换为复频域的 代数方程;求出频域函数后,再做反变换,返回时 域,可求得解,而不需要确定积分常数
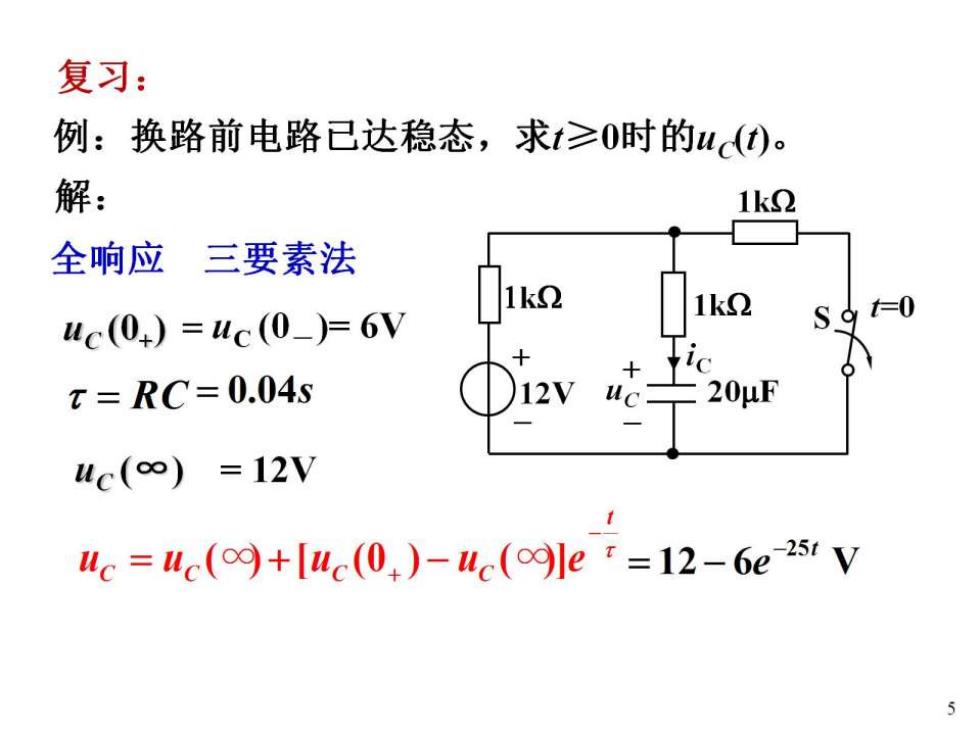
复习: 例:换路前电路已达稳态,求t≥0时的uc(t)。 解: 1k2 全响应 三要素法 1k2 uc(0+)=uc(0_)=6V S=0 x=RC=0.04s 12V 20μF uc(∞)=12V c=uc(o∞+luc(0,)-uc(o∞ler=12-6e2tV 5