
(4)求解联立方程组,得到个支路电流, 需要明确:以上支路电流法求解电路的步骤只适用于电路中每一条支路电压都能用支路电 流表示的情况,若电路中含有独立电流源或受控电流源,因其电压不能用支路电流表示,故不能直 接使用上述步骤。此外,若电路中含有受控源,还应将控制量用支路电流表示,即要多加一个辅助 方程。 3-8 用网孔电流法求解题图3-7中电流,。 解:设网孔电流为.2,其绕行方向如题图3-7中所标。列写网孔方程 「2011-10i2-813=-40 -10in+24i2-4ia=-20 -81n-4i2+20i3=20 应用行列式法解上面方程组 20-10-8 120-10-40 4=1024-4=5104,4,=1024-20=-4880 -8-420 -8-420 所以 注:网孔电流法是以假想的网孔电流作为求解量,它仅适用于平面电路。从本题的求解可以归 纳出用网孔电流法求解电路的步骤是: (1)选取网孔电流2,,如网孔电流方向即认为是列网孔WL方程的绕行方向。 (2)列网孔电流方程。观察电路求自电阻R,R2·(一个网孔中所有电阻之和称该网孔的自 电阻,如本题中R,=202,R2=242,R=202,自电阻总为正值):互电阻R2,R,Rg.(两 网孔公共支路上的电阻之和,如本题中R,=-10,R:=-8,凡=一4,当流过互电阻的两网孔电流 方向一致,互电阻为正值,否则为负值),等效电压源数值(方程右方为各回路中电压源的代数和, 与网孔电流方向一致的电压源前取负号,否则取正号)。 3.9 用回路电流法求解题图3-7中电流·
(4)求解联立方程组,得到个支路电流, 需要明确:以上支路电流法求解电路的步骤只适用于电路中每一条支路电压都能用支路电 流表示的情况,若电路中含有独立电流源或受控电流源,因其电压不能用支路电流表示,故不能直 接使用上述步骤。此外,若电路中含有受控源,还应将控制量用支路电流表示,即要多加一个辅助 方程。 3-8 用网孔电流法求解题图 3-7 中电流 5 i 。 解:设网孔电流为 1, 2 3 , l l l i i i ,其绕行方向如题图 3-7 中所标。列写网孔方程 − − + = − + − = − − − = − 8 4 20 20 10 24 4 20 20 10 8 40 1 2 3 1 2 3 1 2 3 l l l l l l l l l i i i i i i i i i 应用行列式法解上面方程组 4880 8 4 20 10 24 20 20 10 40 5104, 8 4 20 10 24 4 20 10 8 3 = − − − − − − − = = − − − − − − = 所以 i i l 0.956 A 5104 3 4880 5 3 = − − = = = 注:网孔电流法是以假想的网孔电流作为求解量,它仅适用于平面电路。从本题的求解可以归 纳出用网孔电流法求解电路的步骤是: (1)选取网孔电流 1, 2 3 , l l l i i i ,如网孔电流方向即认为是列网孔 KVL 方程的绕行方向。 (2)列网孔电流方程。观察电路求自电阻 11 22 R R, (一个网孔中所有电阻之和称该网孔的自 电阻,如本题中 11 22 33 R R R = = = 20 , 24 , 20 ,自电阻总为正值);互电阻 12 13 23 R R R , , (两 网孔公共支路上的电阻之和,如本题中 12 13 23 R R R = − = − = − 10, 8, 4 ,当流过互电阻的两网孔电流 方向一致,互电阻为正值,否则为负值),等效电压源数值(方程右方为各回路中电压源的代数和, 与网孔电流方向一致的电压源前取负号,否则取正号)。 3-9 用回路电流法求解题图 3-7 中电流 3 i
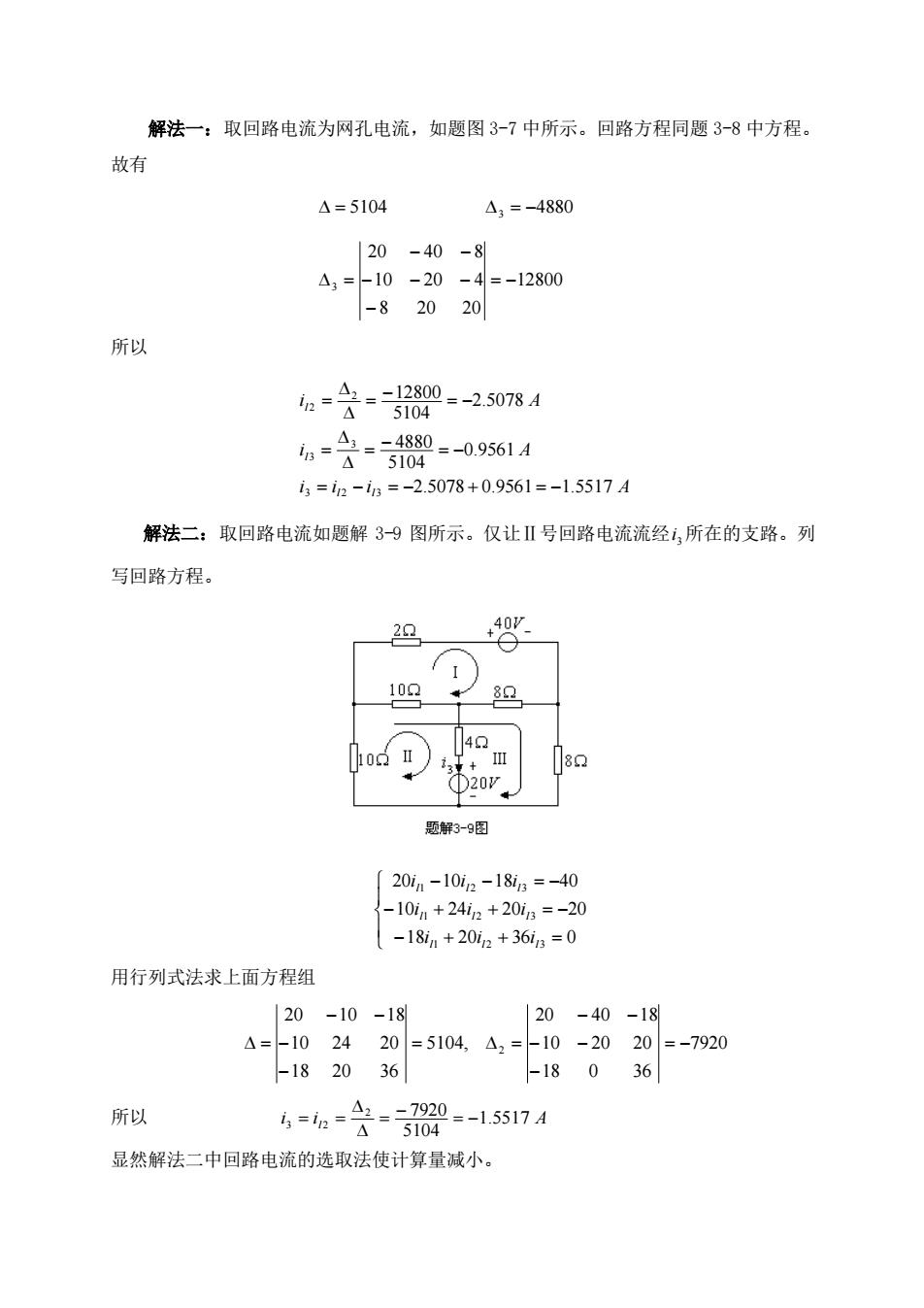
解法一:取回路电流为网孔电流,如题图3-7中所示。回路方程同题3-8中方程。 故有 △=5104 △,=-4880 |20-40-8 43=-10-20-4=-12800 -82020 所以 公=会=器0-250784 h=是=解0=-095614 43=i2-i3=-2.5078+0.9561=-1.5517A 解法二:取回路电流如题解39图所示。仅让Ⅱ号回路电流流经1,所在的支路。列 写回路方程。 20 102 82 20. 题解3-9图 [20in-10i2-18i3=-40 -101n+24i2+20i3=-20 -181n+20i2+361=0 用行列式法求上面方程组 20 -10-18 120-40-18 △=-102420=5104,△2=-10-2020=-7920 -182036 -18036 所以 4=6=会-0-15174 显然解法二中回路电流的选取法使计算量减小
解法一:取回路电流为网孔电流,如题图 3-7 中所示。回路方程同题 3-8 中方程。 故有 = 5104 3 = −4880 12800 8 20 20 10 20 4 20 40 8 3 = − − − − − − − = 所以 i i i A i A i A l l l l 2.5078 0.9561 1.5517 0.9561 5104 4880 2.5078 5104 12800 3 2 3 3 3 2 2 = − = − + = − = − − = = = − − = = 解法二:取回路电流如题解 3-9 图所示。仅让Ⅱ号回路电流流经 3 i 所在的支路。列 写回路方程。 − + + = − + + = − − − = − 18 20 36 0 10 24 20 20 20 10 18 40 1 2 3 1 2 3 1 2 3 l l l l l l l l l i i i i i i i i i 用行列式法求上面方程组 7920 18 0 36 10 20 20 20 40 18 5104, 18 20 36 10 24 20 20 10 18 2 = − − − − − − = = − − − − = 所以 i i l 1.5517 A 5104 2 7920 3 2 = − − = = = 显然解法二中回路电流的选取法使计算量减小

注:回路电流法适用于平面或非平面电路,比网孔法更具灵活性。回路法分析电路时,首先要 确定一组基本回路,表定回路电流的绕行方向,其余步骤与网孔法类似。需要指出的是回路电流法 中两回路的共有支路有时会有多条,因而互有电阻的确定要特别细心。否则会发生遗漏互有电阻的 错误。 3-10 用回路电流法求解题图中52电阻中的电流1。 32 厂4 30 50 62 ①16 ①48 题3-10图 解:选取网孔为基本回路,回路电流的绕行方向如图中所示。列回路方程 [12n-6i2=32-48+16=0 -611+17i2-81a=48 -812+1613=0 应用行列式法 12-60 12-60 4=617-8=1920, 43=-61748=4608 0-816 0-80 所以 3-11 用回路电流法求解图示电路中电压U
注:回路电流法适用于平面或非平面电路,比网孔法更具灵活性。回路法分析电路时,首先要 确定一组基本回路,表定回路电流的绕行方向,其余步骤与网孔法类似。需要指出的是回路电流法 中两回路的共有支路有时会有多条,因而互有电阻的确定要特别细心。否则会发生遗漏互有电阻的 错误。 3-10 用回路电流法求解题图中 5 电阻中的电流 i 。 解:选取网孔为基本回路,回路电流的绕行方向如图中所示。列回路方程 − + = − + − = − = − + = 8 16 0 6 17 8 48 12 6 32 48 16 0 2 3 1 2 3 1 2 l l l l l l l i i i i i i i 应用行列式法 4608 0 8 0 6 17 48 12 6 0 1920, 0 8 16 6 17 8 12 6 0 3 = − − − = = − − − − = 所以 i i l 2.4 A 1920 3 4608 3 = = = = 3-11 用回路电流法求解图示电路中电压 Uo

136r①t40 题3-11图 解:回路电流如图中所标。因3A电流源仅与回路I相关,即有,=3A其余两回 路的方程为 -81n+50i2+10ia=136 -181n+10i2+201a=136-50=86 把n=3A带入两个方程中,加以整理得 50i2+10i3=160 10i2+20=140 解得 2=2A 电压 Un=40×i2=40x2=80V 3-12 用回路电流法求解题3-12图所示电路中电流1,及电压U。 9 2.52 14V 1141 152 解:按图示设网孔电流为回路电流。因受控电流源仅和Ⅲ号回路相关,故有 n-1=6-1=5,对回路I和Ⅱ列方程,并代入i3=-0.in有 ∫34i1-4i2+10×0.1i,=0 -4n+10in+5×0.1in=-420 整理得
解:回路电流如图中所标。因 3A 电流源仅与回路Ⅰ相关,即有, i l1 = 3 A 其余两回 路的方程为 18 10 20 136 50 86 8 50 10 136 1 2 3 1 2 3 − + + = − = − + + = l l l l l l i i i i i i 把 i l1 = 3 A 带入两个方程中,加以整理得 + = + = 10 20 140 50 10 160 2 3 2 3 l l l l i i i i 解得 i l 2 = 2 A 电压 Uo = 40i l2 = 40 2 = 80V 3-12 用回路电流法求解题 3-12 图所示电路中电流 a I 及电压 Uo 。 14V + − 15 I a Uo + − 4 1.4I a 2.5 8 2 解 : 按图示设网孔 电流 为回路 电流 。因受 控电 流源仅 和Ⅲ 号回路 相关 ,故有 n− = − = 1 6 1 5 ,对回路Ⅰ和Ⅱ列方程,并代入 3 1 1 0. l l i = − i 有 − + + = − − + = 4 10 5 0.1 420 34 4 10 0.1 0 1 2 1 1 2 1 l l l l l l i i i i i i 整理得