经典Sobolev空间 定义2.1 设f∈L(2),a∈NP且p∈C洽(2).如果存在一个g∈L1(2)满 足 人=(-1人9k 则称g是f的a阶弱导数. 4口4+4左,4生+主分QC 美芳芳。 第三幸Sobolev空间
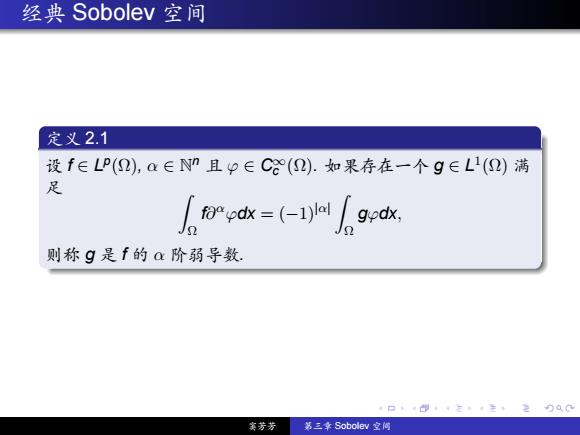
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 经典 Sobolev 空间 定义 2.1 设 f ∈ L p (Ω), α ∈ N n 且 φ ∈ C∞ c (Ω). 如果存在一个 g ∈ L 1 (Ω) 满 足 Z Ω f∂ αφdx = (−1)|α| Z Ω gφdx, 则称 g 是 f 的 α 阶弱导数. 窦芳芳 第三章 Sobolev 空间

定义2.2 设1≤p≤oo,设m≥0为自然数.如果函数f的弱导数8Pf a≤m)存在且属于LP(),则称其是WmP(2)的.如果f在 WmP(2)中,定义f的Wm.P(2)函数为 IIflwn()∑l- l31≤m WP(2)即为LP(2). 对任意k,p,WmP()Wm+1P(2). 例2.1 函数|si在W,°()中,但并不在经典意义下处处可微. 实芳芳 第三章Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 定义 2.2 设 1 ≤ p ≤ ∞, 设 m ≥ 0 为自然数. 如果函数 f 的弱导数 ∂ αf (|α| ≤ m) 存在且属于 L p (Ω),则称其是 Wm,p (Ω) 的. 如果 f 在 Wm,p (Ω) 中, 定义 f 的 Wm,p (Ω) 函数为 ||f||Wm,p(Ω) △ = X |β|≤m ||∂ β f||L p(Ω). W0,p (Ω) 即为 L p (Ω). 对任意 k, p,Wm,p (Ω) ⊃ Wm+1,p (Ω). 例 2.1 函数 |sin x| 在 W1,∞(R) 中, 但并不在经典意义下处处可微. 窦芳芳 第三章 Sobolev 空间

引理2.1 设1≤p<oo,k≥0.则试验函数空间C(R”)是P(R)的 稠密子集。 Schwartz函数空间S(Rn)在WP(Rn)中稠密. 练习2.1 证明引理2.1对p=0时不成立. (提示:设k≥0.证明C2(Rn)在Wk©(R)中的闭包包含于 C(R”)中) 引理2.1总结了试验函数空间C2(R”)是WkP(R)的一个 稠密子集.一般来说,当将R”替换为2时是不对的.这将需要介 绍WP(2),是关于范数|·wmp@的C2(2)的闭包. a 窝芳芳 第三幸Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 引理 2.1 设 1 ≤ p < ∞,k ≥ 0. 则试验函数空间 C∞ c (R n ) 是 Wk,p (R n ) 的 稠密子集. Schwartz 函数空间 S(R n ) 在 Wk,p (R n ) 中稠密. 练习 2.1 证明引理 2.1 对 p = ∞ 时不成立. (提示: 设 k ≥ 0. 证明 C∞ c (R n ) 在 Wk,∞(R n ) 中的闭包包含于 C k (R n ) 中.) 引理 2.1 总结了试验函数空间 C∞ c (R n ) 是 Wk,p (R n ) 的一个 稠密子集. 一般来说, 当将 R n 替换为 Ω 时是不对的. 这将需要介 绍 W m,p 0 (Ω), 是关于范数 | · |Wm,p(Ω) 的 C∞ c (Ω) 的闭包. 窦芳芳 第三章 Sobolev 空间

坐标卡 从WmP(Rn)的性质得到WmP(2)的性质,其中R?有一个 相对简单的边界 令2CR”,边界为n-1维Cm-流形.2(局部)位于边界 02的一侧. 设Q={y∈R”:ly以≤1,1≤j≤n, Qo={y∈Q:yn=0},及Q+={y∈Q:yn>0},可如下计算最 后一个条件: 存在一个R”中的有界开集集合{1≤≤N(如果2无界,N 可为+o∞),使得a2CU{1sjsN;以及相应的有正Jacobian J(9)的函数9j∈Cm(Q,),1≤j≤N,且9j分别是Q,Q+和 Q0到20,2∩2,∩2的双射.对每一j(9,2)是对边界的 一个坐标卡. 实芳芳 第三幸Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 坐标卡 从 Wm,p (R n +) 的性质得到 Wm,p (Ω) 的性质, 其中 R n + 有一个 相对简单的边界. 令 Ω ⊂ R n,边界为 n − 1 维C m-流形. Ω(局部)位于边界 ∂Ω 的一侧. 设 Q = {y ∈ R n : |yj | ≤ 1, 1 ≤ j ≤ n}, Q0 = {y ∈ Q : yn = 0}, 及 Q+ = {y ∈ Q : yn > 0}, 可如下计算最 后一个条件: 存在一个 R n 中的有界开集集合 {Ωj}1≤j≤N (如果 Ω 无界,N 可为 +∞) ,使得 ∂Ω ⊂ S {Ωj}1≤j≤N ;以及相应的有正 Jacobian J(φj) 的函数 φj ∈ C m(Q, Ωj) , 1 ≤ j ≤ N, 且 φj 分别是 Q,Q+ 和 Q0 到 Ω0, Ωj ∩ Ω, Ωj ∩ ∂Ω 的双射. 对每一 j, (φj , Ωj) 是对边界的 一个坐标卡 . 窦芳芳 第三章 Sobolev 空间

给定如上定义的坐标卡集合{(9,)}1≤≤N,构造R”中相应 的开集集合F满足FC及 UF5a9. 1<j<N 定义D0=D及Fo=D\Uh≤swF,则FCo.又注意到 2cQU UF 1≤jsN 及 2cUF 0≤jKN 对每一j,0≤j≤N,设y∈C(R)的选取满足 0≤(x)≤1, x∈Rn, supp(aj)c j a(X)=1, VxE Fj. 实芳芳 第三章Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 给定如上定义的坐标卡集合 {(φj , Ωj)}1≤j≤N, 构造 R n 中相应 的开集集合 Fj 满足 F¯ j ⊂ Ωj 及 [ 1≤j≤N Fj ⊃ ∂Ω. 定义 Ω0 = Ω 及 F0 = Ω \ S 1≤j≤N F¯ j , 则 F¯ 0 ⊂ Ω0. 又注意到 Ω¯ ⊂ Ω ∪ [ 1≤j≤N Fj 及 Ω ⊂ [ 0≤j≤N F¯ j . 对每一 j, 0 ≤ j ≤ N, 设 αj ∈ C∞ c (R n ) 的选取满足 0 ≤ αj(x) ≤ 1, ∀x ∈ R n , supp (αj) ⊂ Ωj , αj(x) = 1, ∀x ∈ F¯ j . 窦芳芳 第三章 Sobolev 空间