
Generating Functions
Generating Functions

Generating Functions: Enumerative Combinatorics "the most useful but most Volume I difficult to understand method RICHARD P.STANLEY (for counting)
“the most useful but most difficult to understand method (for counting)” Generating Functions:

generate ©umerate all subsets of {O,●,Q} (x0+x21)(x0+x1)(x0+2) z0aOx0 +x0xOx1+z0x1x0+x0x1z1 x1x0x0+x1x0x1+x1x1x0+x1x1x1 (1+x)3=1+3x+3x2+x3 coefficient of:of k-subsets
{ , , } enumerate all subsets of generate (x0 + x1)(x0 + x1)(x0 + x1) = + + + + + + + x1 x0x0x0 x0x0x1 x0 x0 x1 x0 x1 x1 x0 x0 x1 x0 x1 x1 x0 x1 x1 x1 x1 (1 + x) 3 =1+3x + 3x2 + x3 coefficient of xk : # of k-subsets

{○,O,○, ●,●,●,O, ○,○,○,○,○} (1+x+x2+x3) (1+x+x2+x3+x4) (1+x+x2+x3+x4+x5) 三 1+3+6x2+10x3+14x4+17x5+18x6 +17x7+14x8+10x9+6x10+3x11+x12
(1 + x + x2 + x3) (1 + x + x2 + x3 + x4) (1 + x + x2 + x3 + x4 + x5) { } , , , , , , , , , , , = 1+3+6x2 + 10x3 + 14x4 + 17x5 + 18x6 +17x7 + 14x8 + 10x9 + 6x10 + 3x11 + x12
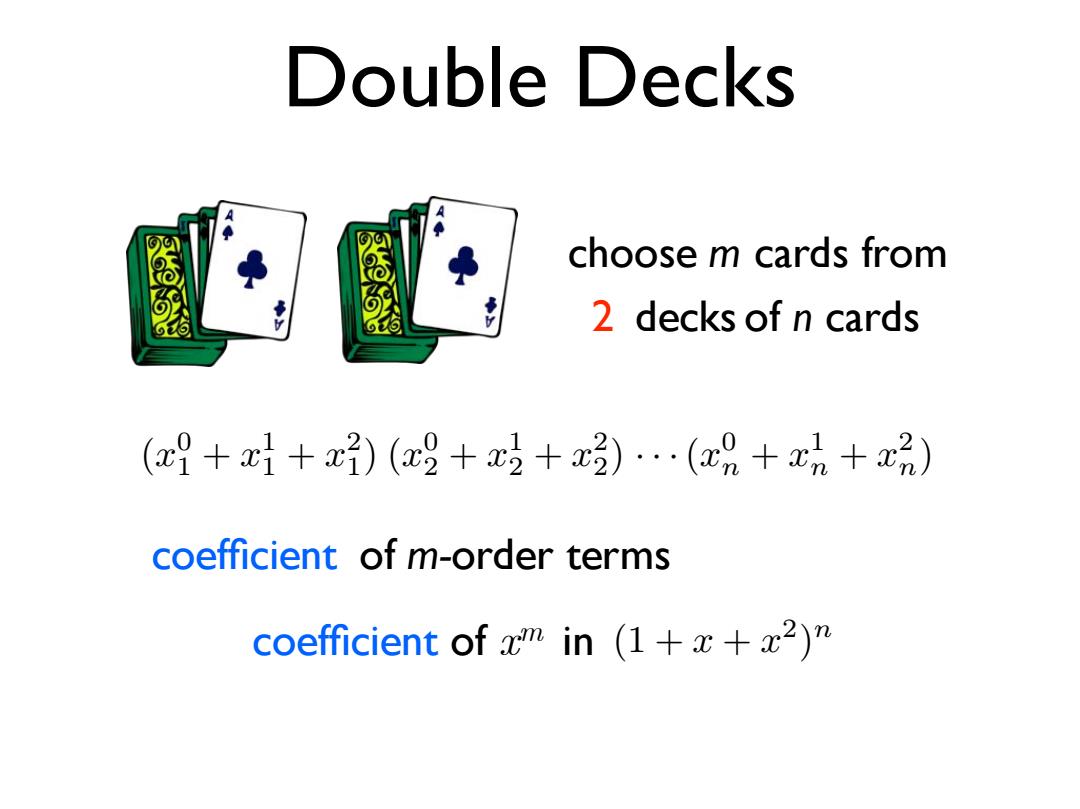
Double Decks choose m cards from 2 decks of n cards (+1+x)(唱+2+x)…(a%+x%+x品) coefficient of m-order terms coefficient of xmm in (1+x+x2)
coefficient Double Decks (x0 1 + x1 1 + x2 1) (x0 2 + x1 2 + x2 2) ···(x0 n + x1 n + x2 n) of m-order terms (1 + x + x2) n coefficient of xm in 2 deck of s n cards choose m cards from