
则可计算出各支路电压电流分别为 4。=4。=g×20=1×20=20V 42=42=×(4+20)=1x24=24y i4==02/12=24/12=2A 3=1=i+i,=2+1=3A u1=w1=1×5+42=3×5+24=39V 1==+6=1+3=4A 4=,=×4+a1=4×4+39=55V 即当激励4,=4,=55时,各电压、电流如以上计算数值,现给定4,=10V, 相当于将以上激励(缩小了号倍,即K一品 102 故电路各支路的电流和结点电压应同时缩小二倍,有 4=-品4=音=04 M=k=子×39=78y 2 11 2 40 输出电压和激励的比值为= 注:本题的计算采用“倒退法”,即先从梯形电路最远离电源的一端开始,对 电压或电流设一便于计算的值,倒退算至激励处,最后再按齐性定理予以修正。 4-7 图示电路中,当电流源和电压源4反向时(4,不变),电压4是原 来的0.5倍当i和42反向时(4不变),电压4是原来的0.3倍。问:
则可计算出各支路电压电流分别为 ' ' 5 ' ' 2 2 5 ' ' 4 4 2 ' ' ' 3 3 4 5 ' ' ' 1 1 3 2 ' ' ' 1 1 2 3 ' ' ' 1 1 20 1 20 20 (4 20) 1 24 24 /12 24 /12 2 2 1 3 5 3 5 24 39 1 3 4 4 4 4 39 55 o o n n n n n n s s n u u i V u u i V i i u A i i i i A u u i u V i i i i A u u i u V = = = = = = + = = = = = = = = + = + = = = + = + = = = + = + = = = + = + = 即当 激 励 ' us = us = 55V 时,各 电 压、电流 如 以 上计 算 数值 ,现 给 定 us = 10 V, 相当于将以上激励 ' s u 缩 小了 55 10 倍 ,即 11 2 55 10 K = = 故电路各支路的电流和结点电压应同时缩小 11 2 倍, 有 ' 1 1 ' 2 2 ' 3 3 ' 4 4 ' 5 5 ' 1 1 ' 2 2 ' 2 8 4 0.727 11 11 2 2 1 11 11 2 6 3 11 11 2 4 2 11 11 2 2 1 11 11 2 78 39 11 11 2 48 24 11 11 2 40 20 11 11 n n n n o o i Ki A i Ki A i Ki A i Ki A i Ki A u Ku V u Ku V u Ku V = = = = = = = = = = = = = = = = = = = = = = = = = 输出电压和激励的比值为 40 4 11 0.364 10 11 o s u u = = = 注 : 本题 的 计 算 采用 “ 倒 退 法”, 即 先从 梯 形 电 路 最远 离 电 源 的 一端 开 始 ,对 电压或电流设一便于计算的值,倒退算至激励处,最后再按齐性定理予以修正 。 4-7 图 示 电 路 中 , 当电 流 源 s1 i 和电压源 s1 u 反向时( s2 u 不 变), 电 压 ab u 是 原 来的 0 .5 倍 ;当 s1 i 和 s2 u 反向 时 ( s1 u 不变), 电压 ab u 是 原 来的 0.3 倍 。问 :
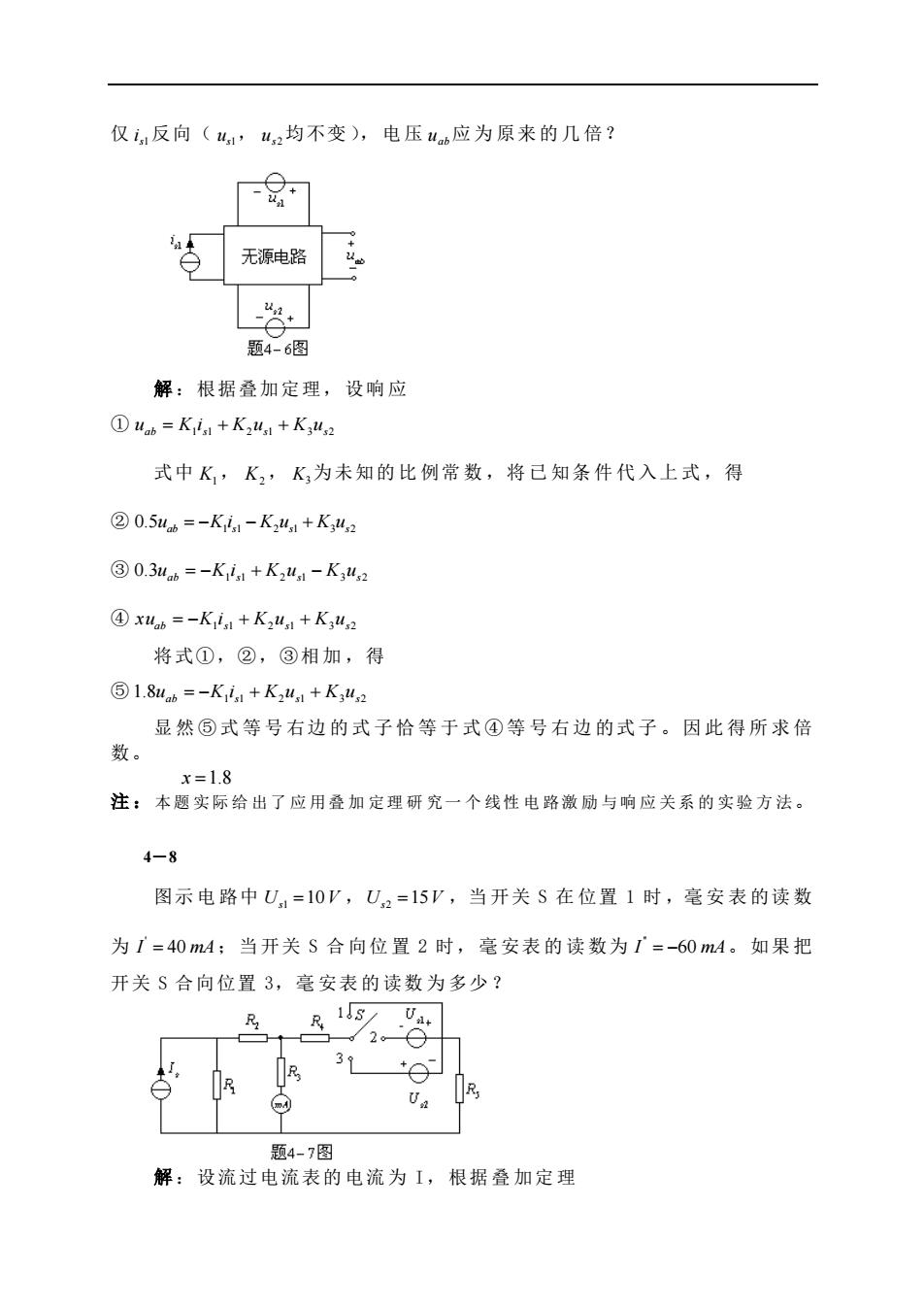
仅i,反向(41,42均不变),电压4s应为原来的几倍? 无源电路 题4-6图 解:根据叠加定理,设响应 ①ub=K1+K4,1+Kg4a 式中K,K2,K为未知的比例常数,将己知条件代入上式,得 ②0.5u=-K1-K41+K4 ③0.3b=-K41+K41-K42 ④x4a=-K1+K241+K,42 将式①,②,③相加,得 同1.86=-K1+K,41+K42 显然⑤式等号右边的式子恰等于式④等号右边的式子。因此得所求倍 数。 x=1.8 注:本题实际给出了应用叠加定理研究一个线性电路激励与响应关系的实验方法。 48 图示电路中U=10V,U2=15V,当开关S在位置1时,毫安表的读数 为1=40m4:当开关S合向位置2时,毫安表的读数为1=-60m4。如果把 开关S合向位置3,毫安表的读数为多少? 3+△ Ua 题4-7图 解:设流过电流表的电流为【,根据叠加定理
仅 s1 i 反向( s1 u , s2 u 均不变 ), 电 压 ab u 应 为 原来 的 几 倍? 解 :根据叠加定理,设响应 ① ab 1 s1 K2us1 K3us2 u = K i + + 式中 K1, K2, K3 为未知的 比 例常 数 ,将 已 知条 件 代 入上 式 ,得 ② 1 1 2 1 3 2 0.5 ab s s s u K i K u K u = − − + ③ 3 1 1 2 1 3 2 0. ab s K us K us u = −K i + − ④ ab 1 s1 K2us1 K3us2 xu = −K i + + 将式①,②,③相 加 ,得 ⑤ 8 1 1 2 1 3 2 1. ab s K us K us u = −K i + + 显 然 ⑤ 式 等 号 右边 的 式 子 恰 等 于 式 ④ 等 号 右 边 的式 子 。 因 此 得 所 求 倍 数。 x =1.8 注 : 本题 实际 给 出了 应 用叠 加 定理 研 究一 个 线性 电 路激 励 与响 应 关系 的 实验 方 法。 4-8 图示 电 路中 1 10 U V s = , 2 15 U V s = ,当 开关 S 在 位置 1 时 ,毫 安 表 的读 数 为 ' I mA = 40 ;当 开关 S 合 向位 置 2 时, 毫 安表 的 读 数为 '' I mA = −60 。 如果 把 开关 S 合向位置 3,毫 安表 的 读数 为 多少 ? 解 :设流过电流表的电流为 I, 根据 叠 加定 理

I=K 1,+KU, 当开关S在位置1时,相当于U,=0,当开关S在位置2时,相当于 U,=U, 当开关S在位置3时,相当于U,=-U2,把上述条件代入以上方程式中, 可 得关系式 40=K,L, -60=K1,+KU1=40+K2×10 从中解出 10 所以当S在位置3时,有1=Kl,+K,(U2)=40+(-10)x(-15)=190m4 4-9 求图示电路的戴维宁和诺顿等效电路。 手92950里22 A 22 60 1024e 。b (a) (a解: 2 a a 29 42 22 20 6 025A 1) (2) (3) 求开路电压Wc。设w参考方向如图所示,由KVL列方程 (2+4)1+3+2(1-1)=0 解得 4=4×1=4x(-3)=-0.5 求等效内阻R·
1 2 s s I K I K U = + 当开 关 S 在 位置 1 时, 相 当于 Us = 0 , 当开 关 S 在 位置 2 时 ,相 当 于 Us = Us1, 当开 关 S 在 位置 3 时 ,相 当 于 U U s s = − 2 ,把 上述 条 件 代入 以 上方 程 式中 , 可 得关系式 60 40 10 40 1 2 1 2 1 − = + = + = K I K U K K I s s s 从中解出 10 10 100 2 = − − K = 所以当 S 在位置 3 时,有 1 2 2 ( ) 40 ( 10) ( 15) 190 s s I K I K U mA = + = + − − = 4-9 求图示电路的戴维宁和诺顿等效电路。 (a) (b) (a)解 : (1) (2) (3) 求开路电压 oc u 。设 oc u 参考方向如图所示,由 KVL 列方程 (2 + 4)I + 3+ 2(I −1) = 0 解得 I A 8 1 = − uoc I ) 0.5V 8 1 = 4 = 4 (− = − 求等效内阻 Req

将原图中电压源短路,电流源开路,电路变为题解4一8(a)图,应用 电阻串并联等效,求得 R=(2+2)/4=22 画出戴维宁等效电路如图(b)所示,应用电源等效变换得诺顿等效电 路如图(c)所示。 其中 -元-950254 注意画等效电路时不要将开路电压u的极性画错,本题设a端为4s的 “+”极性端,求得的u®为负值,故(b)图中的b端为开路电压的实际“+” 极性端。 (b) 1929472222 l62 1024x 1 解:本题电路为梯形电路,根据齐性定理,应用“倒退法”求开路电 压u。设4=W=I0V,各支路电流如图示,计算得 4=4=8=14 n2=42=(2+10)x1=12 i,=i=2=是-244 4=6=+5=2.4+1=3.4A 4a==7×+42=7x3.4+12=35.8y 4=6=4-358-5967A 6 1=+4=5.967+3.4=9.367A 4=4,=9×+4=9×9.367+35.8=120.1V 故当4,=5V时,开路电压4为 5 Me=K=12×10=04160 将电路中的电压源短路,应用电阻串并联等效,求得等效内阻R为 R=[(9∥6+7)∥5+2]110=3.5052
将原 图 中电 压 源短 路,电 流源 开 路,电路 变 为 题解 4-8(a)图,应 用 电阻串并联等效,求得 Req =(2+2)//4=2 画出 戴 维宁 等 效电 路 如图( b)所 示 ,应 用电 源 等效 变 换得 诺 顿等 效 电 路如图(c)所示 。 其中 A R u I eq oc sc 0.25 2 0.5 = − − = = 注意 画 等效 电 路时 不 要将 开 路电 压 oc u 的极 性 画 错,本题 设 a 端 为 oc u 的 “+ ”极 性端 ,求 得的 oc u 为 负值 ,故(b)图 中的 b 端 为开 路 电压 的 实际“ +” 极性端。 (b) 解 : 本 题 电 路 为梯 形 电 路 , 根 据 齐 性 定 理 , 应用 “ 倒 退 法 ” 求 开 路电 压 oc u 。设 ' 10 oc oc u u V = = ,各支路电 流 如图 示 ,计 算 得 ' 5 5 ' 2 2 ' ' 2 4 4 ' ' ' 3 3 4 5 ' ' 1 1 3 2 ' 1 2 2 ' ' 1 2 3 ' ' 1 1 10 1 10 (2 10) 1 12 12 2.4 5 5 2.4 1 3.4 7 7 3.4 12 35.8 35.8 5.967 6 6 5.967 3.4 9.367 9 9 9.367 35.8 120.1 n n n n n n n s s n i i A u u V u i i A i i i i A u u i u V u i i A i i i A u u i u = = = = = + = = = = = = = + = + = = = + = + = = = = = = + = + = = = + = + = V 故当 5 s u V = 时,开路电压 oc u 为 ' 5 10 0.416 12.1 oc oc u Ku V = = = 将电路中的电压源短路,应用电阻串并联等效,求得等效内阻 R eq 为 [(9 // 6 7) // 5 2]//10 3.505 R eq = + + =