
【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“V,错误 的画“X” ()若一条直线平行于一个平面,则这条直线平行于这个平面 内的任一条直线.(X) (2)如果一个平面内的两条直线平行于另一个平面,那么这两 个平面平行.(X) (3)如果两个平面平行,那么分别在这两个平面内的两条直线 平行或异面.(√) (4)若平面a∥平面B,直线mcf,则m∥a(√)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√” ,错误 的画“×” . (1)若一条直线平行于一个平面,则这条直线平行于这个平面 内的任一条直线.( ) (2)如果一个平面内的两条直线平行于另一个平面,那么这两 个平面平行.( ) (3)如果两个平面平行,那么分别在这两个平面内的两条直线 平行或异面.( ) (4)若平面α∥平面β,直线m⊂β,则m∥α.( ) × × √ √
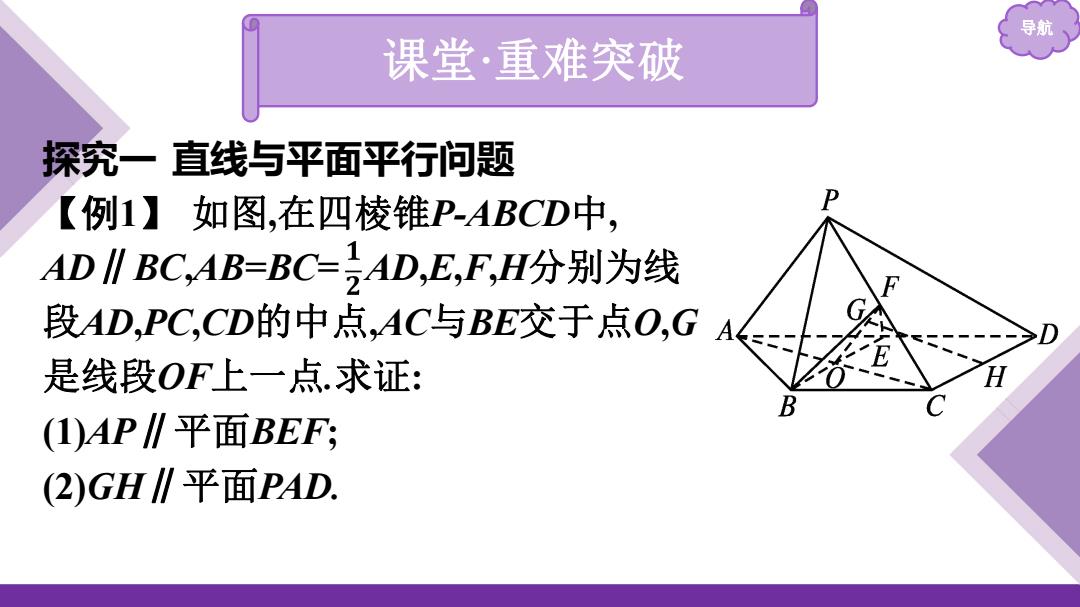
导航 课堂·重难突破 探究一直线与平面平行问题 【例1】如图,在四棱锥P-ABCD中, AD∥BC,AB=BC=)AD,E,F,H分别为线 段AD,PC,CD的中点,AC与BE交于点O,G A 是线段OF上一点.求证: B (1)AP∥平面BEF; 2)GH∥平面PAD
导航 课堂·重难突破 探究一 直线与平面平行问题 【例1】 如图,在四棱锥P-ABCD中, AD∥BC,AB=BC= AD,E,F,H分别为线 段AD,PC,CD的中点,AC与BE交于点O,G 是线段OF上一点.求证: (1)AP∥平面BEF; (2)GH∥平面PAD
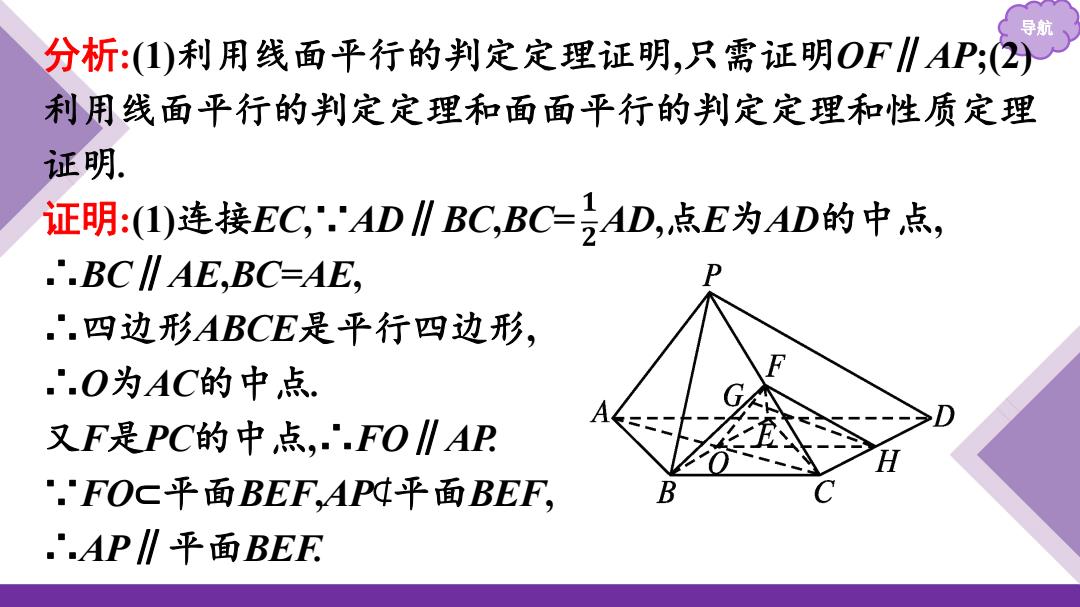
导期 分析:(1)利用线面平行的判定定理证明,只需证明OF∥AP;(2 利用线面平行的判定定理和面面平行的判定定理和性质定理 证明. 证明:(1)连接EC,.'AD∥BC,BC-=AD,点E为AD的中点, .'.BC∥AE,BC=AE, .'.四边形ABCE是平行四边形, ..O为AC的中点. A 叉F是PC的中点,∴.FO∥AP "."FOC平面BEF,AP¢平面BEF, .'.AP∥平面BEF
导航 分析:(1)利用线面平行的判定定理证明,只需证明OF∥AP;(2) 利用线面平行的判定定理和面面平行的判定定理和性质定理 证明. 证明:(1)连接EC,∵AD∥BC,BC= AD,点E为AD的中点, ∴BC∥AE,BC=AE, ∴四边形ABCE是平行四边形, ∴O为AC的中点. 又F是PC的中点,∴FO∥AP. ∵FO⊂平面BEF,AP⊄平面BEF, ∴AP∥平面BEF

导航 (2)连接FH,OH,"."点F,H分别是PC,CD的中点, .FH∥PD.又FHt平面PAD,PDC平面PAD, .FH∥平面PAD. "O是AC的中点,H是CD的中点, .'.OH∥AD.又OH平面PAD,ADC平面PAD, .'.OH∥平面PAD. 又FH∩OH=H,且FH,OHc平面OHF, .".平面OHF∥平面PAD. 又GHc平面OHF,.∴.GH∥平面PAD
导航 (2)连接FH,OH,∵点F,H分别是PC,CD的中点, ∴FH∥PD.又FH⊄平面PAD,PD⊂平面PAD, ∴FH∥平面PAD. ∵O是AC的中点,H是CD的中点, ∴OH∥AD.又OH⊄平面PAD,AD⊂平面PAD, ∴OH∥平面PAD. 又FH∩OH=H,且FH,OH⊂平面OHF, ∴平面OHF∥平面PAD. 又GH⊂平面OHF,∴GH∥平面PAD

导航 反思感悟 证明线面平行的方法:(1)线面平行的定义;2)线面平行的判定 定理;3)面面平行的性质(a∥B,acaa∥)
导航 证明线面平行的方法:(1)线面平行的定义;(2)线面平行的判定 定理;(3)面面平行的性质(α∥β,a⊂α⇒a∥β)