第一布里渊区里的色散关系: (q】 0=1 ★分离原子集体振动形成的格 波与连续介质中的弹性波相比,色 散关系发生了色散,偏离了线性关 系,而且具有周期性和反射对称性 2π o(g+2m)=o(g) o(q)=o(-q) 在波矢空间 ★从解的表达式中可以看出:把aq改变2π的整数倍后, 所有原子的振动实际上没有任何区别,因此有物理意义的q取 值范围可以限制在第一布里渊区内。 元 元 -π≤ag<π 1<十 a 这就避免了某一频率的格波有很多波长与之对应的问题 这种性质称作格波的简约性。 2π 一 维单原子链的倒格矢: a
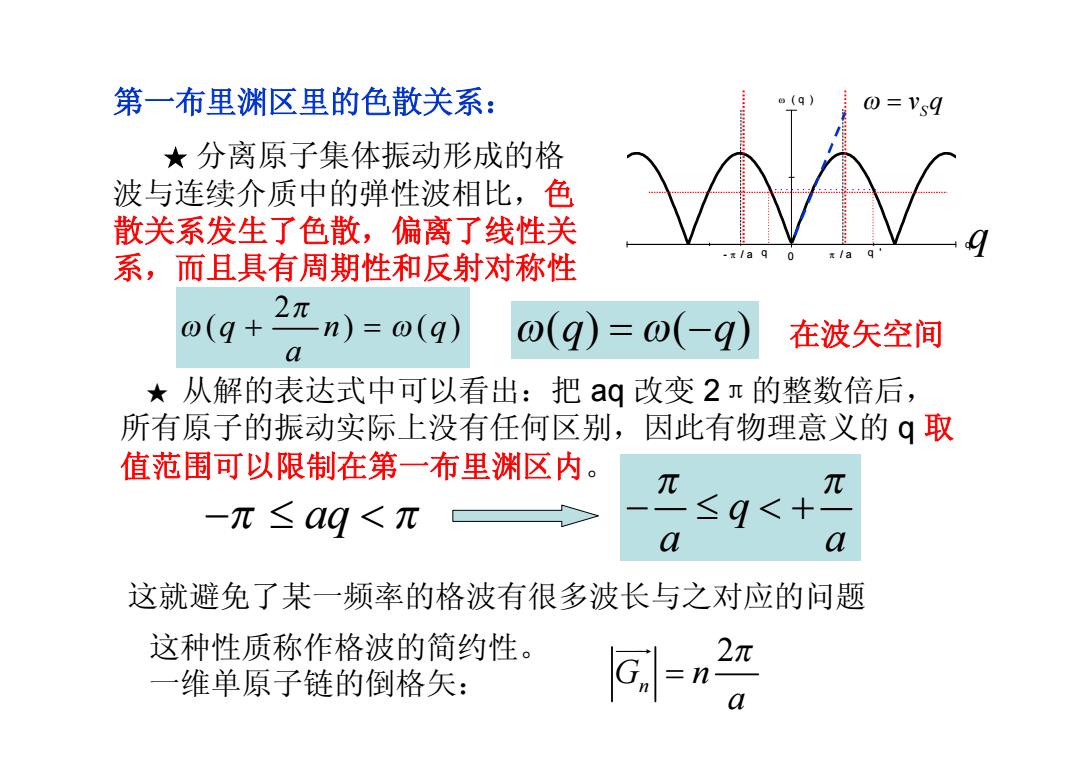
第一布里渊区里的色散关系: ★ 分离原子集体振动形成的格 波与连续介质中的弹性波相比,色 散关系发生了色散,偏离了线性关 系,而且具有周期性和反射对称性 q q ' 0 q w ( q ) - p / a p / a S w = v q 2 (q n q ) ( ) a p w w + = w w (q q ) = -( ) q ★ 从解的表达式中可以看出:把 aq 改变 2π的整数倍后, 所有原子的振动实际上没有任何区别,因此有物理意义的 q 取 值范围可以限制在第一布里渊区内。 -p p £ < aq q a a p p - £ < + 这种性质称作格波的简约性。 一维单原子链的倒格矢: 2 G n n a p = uur 在波矢空间 这就避免了某一频率的格波有很多波长与之对应的问题
入=4a 2π 9= 2a 4 参考黄昆书p85图 2π 5π 92 2a ·: 2 a : a 3 : a : 由图明显看出两个不同波长的格波只表示晶体原子的一 种振动状态,q只需要在第一布里渊区内取值即可,这是与 连续介质弹性波的重大区别
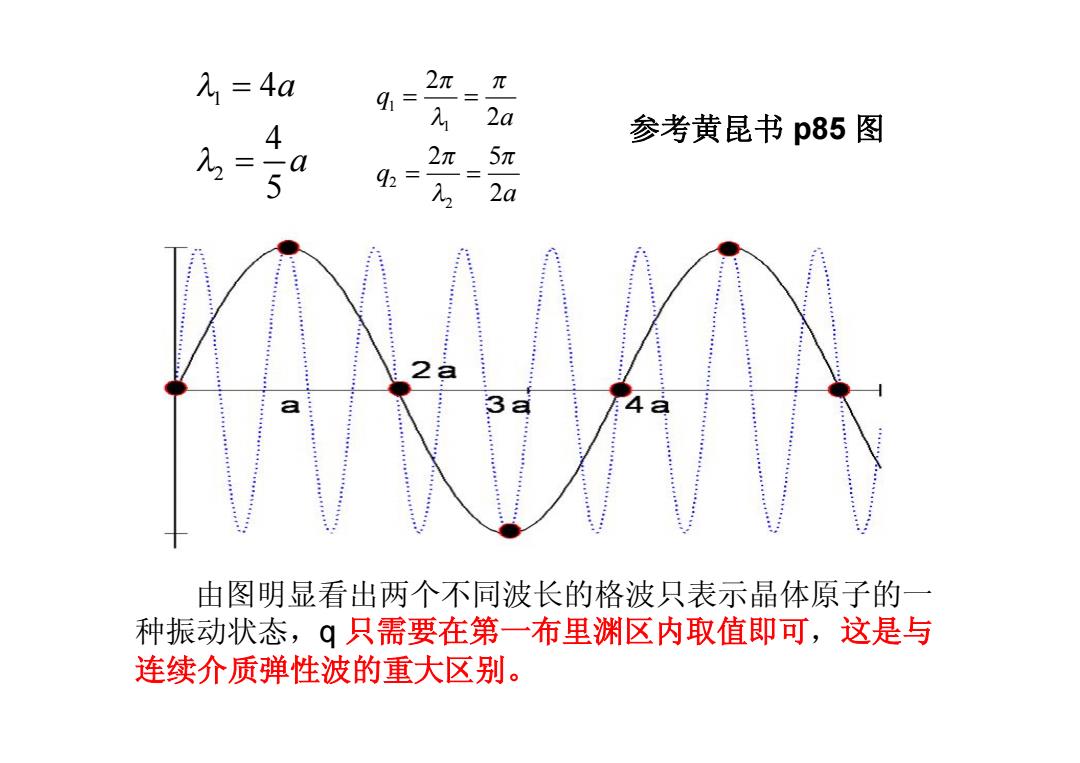
由图明显看出两个不同波长的格波只表示晶体原子的一 种振动状态,q 只需要在第一布里渊区内取值即可,这是与 连续介质弹性波的重大区别。 1 2 4 4 5 a a l l = = 1 1 2 2 2 2 2 5 2 q a q a p p l p p l = = = = 参考黄昆书 p85 图
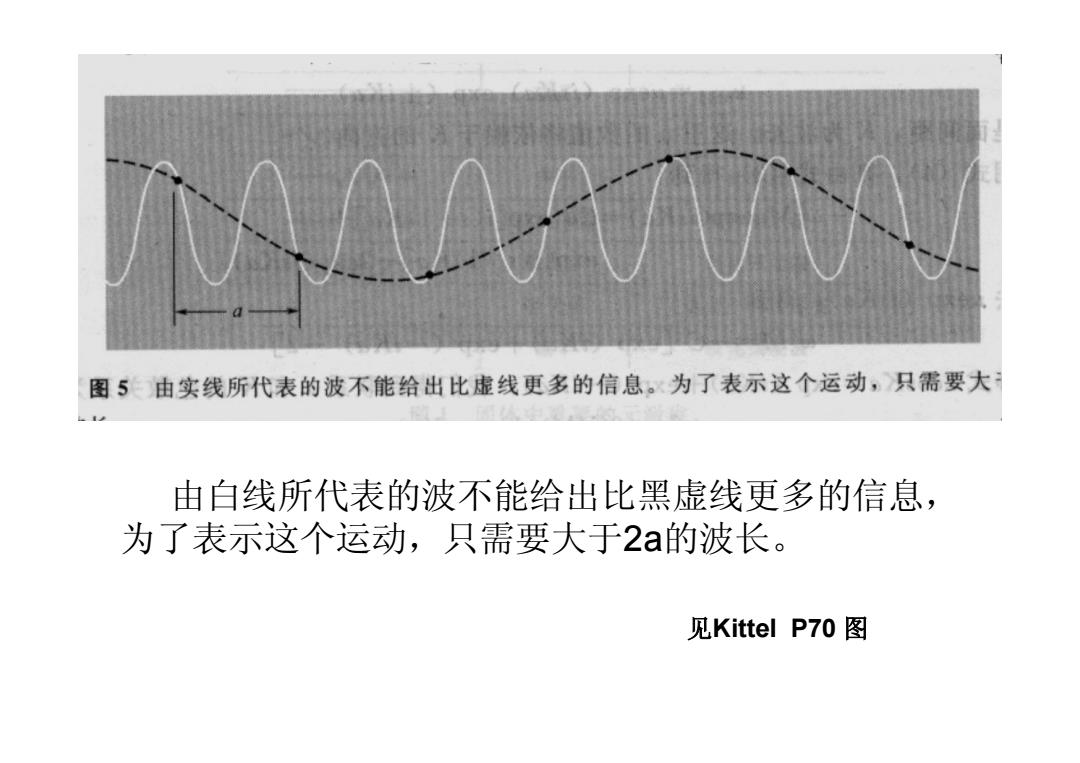
图5由实线所代表的波不能给出比虚线更多的信息。为了表示这个运动,只需要大 由白线所代表的波不能给出比黑虚线更多的信息, 为了表示这个运动,只需要大于2a的波长。 见Kittel P70图
由白线所代表的波不能给出比黑虚线更多的信息, 为了表示这个运动,只需要大于2a的波长。 见Kittel P70 图

周期性边界条件(Borm一Karman边界条件) 上面求解假定原子链无限长,这是不现实的,确定何种边界 条件才既能使运动方程可解,又能使结果符合实际晶体的测量结 果呢?Born一Karman最早利用周期性边界条件解决了此问 题,成为固体理论的一个典范。 所谓周期性边界条件就是将一有限长度的晶体链看成无限长 晶体链的一个重复单元,即:4w=4, Aeto-(Nn)ag]=der(or-nag) 即:ea=1 2π n=任意整数,但考虑到q值的取值范围,n取值 Na 数目是有限的:只有布里渊区内的N个整数值。 π 2 n< π N ≤n< a Na a 2 2 周期性边界条件并没有改变方程解的形式,只是对解提出一 定的条件,q只可取N个不同的值,每个q对应着一个格波
周期性边界条件(Born-Karman 边界条件) m N + n = m n 上面求解假定原子链无限长,这是不现实的,确定何种边界 条件才既能使运动方程可解,又能使结果符合实际晶体的测量结 果呢? Born-Karman 最早利用周期性边界条件解决了此问 题,成为固体理论的一个典范。 所谓周期性边界条件就是将一有限长度的晶体链看成无限长 晶体链的一个重复单元,即: i t (N n)aq i( t naq) Ae Ae é ù ë û w - + w - = =1 - iNaq 即:e 2 q n Na p \ = × n =任意整数,但考虑到 q 值的取值范围,n 取值 数目是有限的:只有布里渊区内的 N 个整数值。 2 n a Na a p p p - £ < 2 2 N N \- £ < n 周期性边界条件并没有改变方程解的形式,只是对解提出一 定的条件,q 只可取N个不同的值,每个q对应着一个格波

引入周期性边界条件后,波数q不能任意取值,只能取分 2π 立的值。在g轴上,相邻两个g的取值相距 Na 2π 即在g轴上,每一个g的取值所占的空间为: Na 所以,g值的分布密度(单位长度上的模式数目): p(g)= Na L L=Na为晶体链的长度。 2π 2π 第一布里渊区中波数▣的取值总数等于晶体链的原胞个数, 即:晶格振动格波的总数=N1=晶体链的总自由度数。 a p(q)- 2 Na =N π a 2n 至此,我们可以有把握的说找到了原子链的全部振动模
引入周期性边界条件后,波数 q 不能任意取值,只能取分 立的值。在 q 轴上,相邻两个 q 的取值相距 , 即在 q 轴上,每一个 q 的取值所占的空间为: Na 2p Na 2p 所以,q 值的分布密度(单位长度上的模式数目): ( ) 2 2 Na L r q p p = = L=Na 为晶体链的长度。 第一布里渊区中波数 q 的取值总数等于晶体链的原胞个数, 即:晶格振动格波的总数 =N·1= 晶体链的总自由度数。 2 2 ( ) 2 Na q N a a p p r p = = 至此,我们可以有把握的说找到了原子链的全部振动模