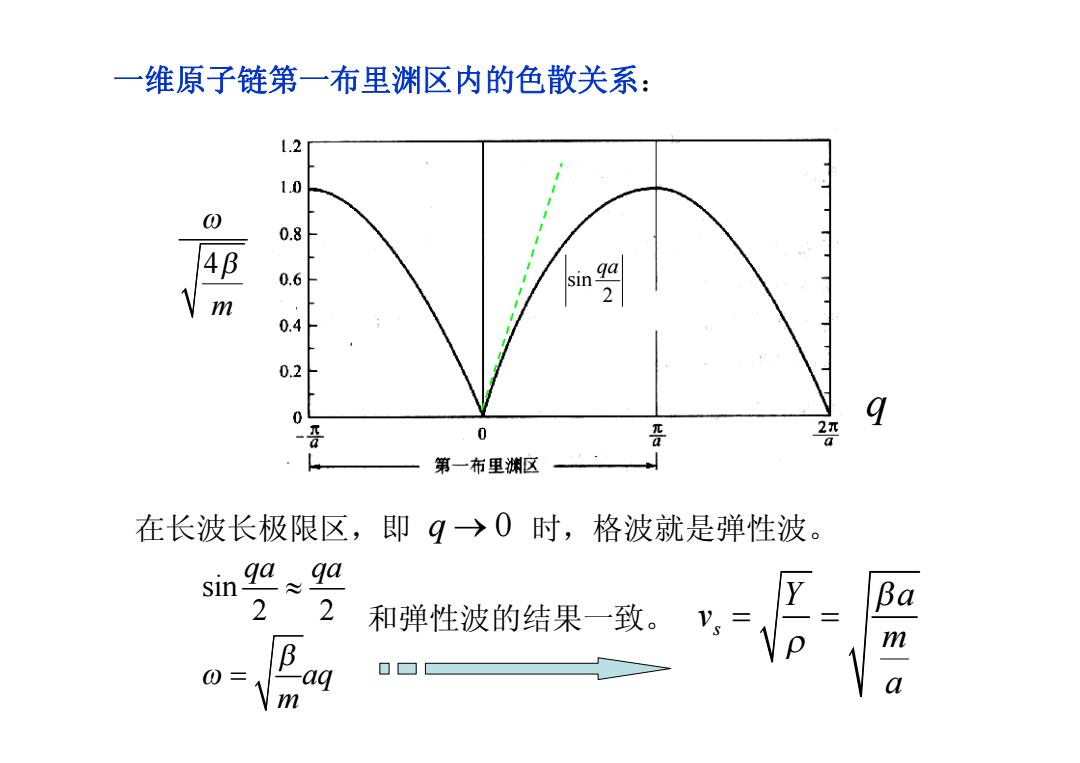
一 维原子链第一布里渊区内的色散关系: 1.2 1.0 0.8 4B 0.6 m 2 0.4 0.2 0 9 0 晋 2 第一布里渊区 在长波长极限区,即9→0时,格波就是弹性波。 sin ga ga 2 2 和弹性波的结果一致。V。= m m
4 m w b 一维原子链第一布里渊区内的色散关系: q sin 2 qa 在长波长极限区,即 q ® 0 时,格波就是弹性波。 sin 2 2 qa qa aq m b w » = s Y a v m a b r 和弹性波的结果一致。 = =

随着q的增长,⊙数值逐渐偏离线性关系,变得平缓, 在布里渊区边界,格波频率达到极大值。 9→元 4B 0→0max a m 相速和群速: 相速度V是单色波单位时间内一定的振动位相所传播的 距离。群速度V是平均频率为ω,平均波矢为q的波包的 传播速度,它是合成波能量和动量的传播速度。 dω p=f= dq 在9→0的长波极限下:Vp=Vg=V 即声速
随着 q的增长,ω数值逐渐偏离线性关系,变得平缓, 在布里渊区边界,格波频率达到极大值。 q a p ® ± max 4 m b w w ® = 相速和群速: 相速度 是单色波单位时间内一定的振动位相所传播的 距离。群速度 是平均频率为ω,平均波矢为q 的波包的 传播速度,它是合成波能量和动量的传播速度。 p v f q w = l × = p v q v d d q v q w = 在 q ® 0 的长波极限下: p q s v = = v v 即声速
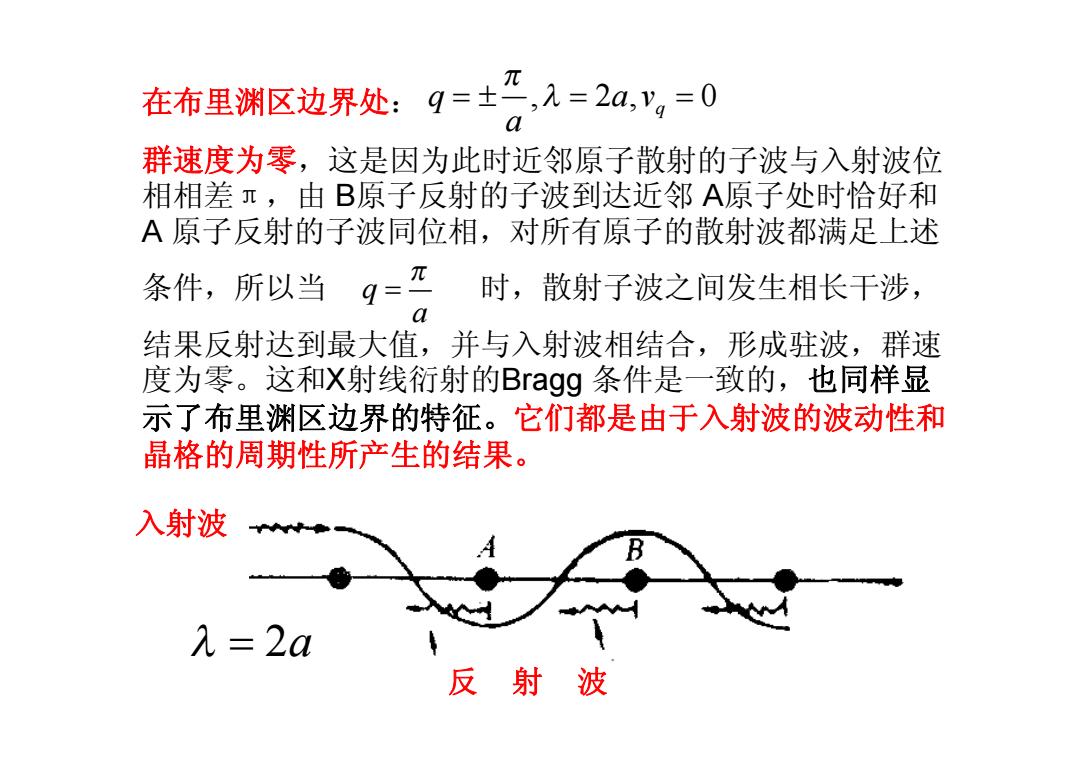
在布里渊区边界处:q=±元,入=2a,y,=0 a 群速度为零,这是因为此时近邻原子散射的子波与入射波位 相相差,由B原子反射的子波到达近邻A原子处时恰好和 A原子反射的子波同位相,对所有原子的散射波都满足上述 条件,以当 q-1 时,散射子波之间发生相长干涉, 结果反射达到最大值,并与入射波相结合,形成驻波,群速 度为零。这和X射线衍射的Bragg条件是一致的,也同样显 示了布里渊区边界的特征。它们都是由于入射波的波动性和 晶格的周期性所产生的结果。 入射波 λ=2a 反射波
在布里渊区边界处: , 2 , 0 q q a v a p = ± l = = 群速度为零,这是因为此时近邻原子散射的子波与入射波位 相相差π,由 B原子反射的子波到达近邻 A原子处时恰好和 A 原子反射的子波同位相,对所有原子的散射波都满足上述 条件,所以当 时,散射子波之间发生相长干涉, 结果反射达到最大值,并与入射波相结合,形成驻波,群速 度为零。这和X射线衍射的Bragg 条件是一致的,也同样显 示了布里渊区边界的特征。它们都是由于入射波的波动性和 晶格的周期性所产生的结果。 入射波 反 射 波 l = 2a q a p =
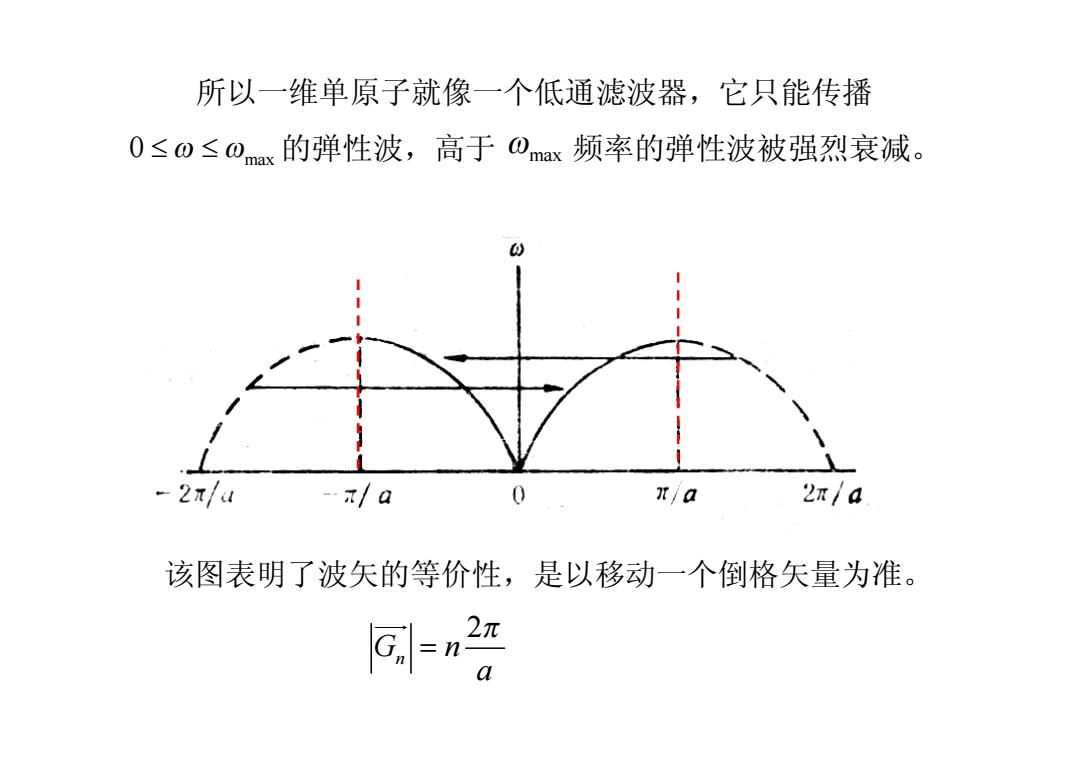
所以一维单原子就像一个低通滤波器,它只能传播 0≤o≤ox的弹性波,高于Omax频率的弹性波被强烈衰减。 -2πu nia 2n/a 该图表明了波矢的等价性,是以移动一个倒格矢量为准
所以一维单原子就像一个低通滤波器,它只能传播 0 £ £ w wmax 的弹性波,高于 wmax 频率的弹性波被强烈衰减。 该图表明了波矢的等价性,是以移动一个倒格矢量为准。 2 G n n a p = uur