
第二章晶体结合 2.1晶体中的结合力和结合能; 2.2 元素和化合物晶体结合的规律性; 2.3弹性应变和晶体中的弹性波; 本章介绍原子、分子是以怎样相互作用结合成晶 体的。晶体结合的方式与固体的结构以及物理化学性 质都有密切关系,因此确定晶体的结合形式也是研究 材料性质的基础。 说明:晶体结合力的研究主要考虑价电子行为,更多的是化学问题,这里 只作为基础知识,简单介绍一些涉及到的物理问题。弹性一节十分重要, 既是学习晶格振动理论的必要基础,又对理解晶体力学性质很有帮助。 (Kittel书5版删掉此节,7版之后又恢复充分说明它的重要性) 参考:黄昆《固体物理学》第2章p49-77 Kittel8版第3章p36-66
第二章 晶体结合 2.1 晶体中的结合力和结合能; 2.2 元素和化合物晶体结合的规律性; 2.3 弹性应变和晶体中的弹性波; 参考:黄昆《固体物理学》 第2章p49-77 Kittel 8版 第3章 p36-66 说明:晶体结合力的研究主要考虑价电子行为,更多的是化学问题,这里 只作为基础知识,简单介绍一些涉及到的物理问题。弹性一节十分重要, 既是学习晶格振动理论的必要基础,又对理解晶体力学性质很有帮助。 (Kittel 书5版删掉此节,7版之后又恢复充分说明它的重要性) 本章介绍原子、分子是以怎样相互作用结合成晶 体的。晶体结合的方式与固体的结构以及物理化学性 质都有密切关系,因此确定晶体的结合形式也是研究 材料性质的基础

2.1晶体的结合力和结合能 一.晶体结合的一般概念 二.晶体的弹性性质 一.晶体结合的一般概念: 三.晶体结合的基本类型 四.离子晶体的结合能 自然界的矿物中绝大多 五.分子晶体的结合能 数物质都以晶态存在,说明 晶体的能量比构成晶体的粒 子处在自由状态时的能量总 和要低的多,因此可以给出: En=EN-Uo Uo是晶体在OK时的总能量,EN是N个自由粒子能量之和, 因此Eb是0K时把晶体分解为相距无限远、静止的中性自由 原子所需要的能量,称作内聚能(Cohesive energy)或结 合能(binding energy)。取EN=O,做能量基点,则有: E6=-U
2.1 晶体的结合力和结合能 一. 晶体结合的一般概念: 一.晶体结合的一般概念 二.晶体的弹性性质 三. 晶体结合的基本类型 四. 离子晶体的结合能 自然界的矿物中绝大多 五. 分子晶体的结合能 数物质都以晶态存在,说明 晶体的能量比构成晶体的粒 子处在自由状态时的能量总 和要低的多,因此可以给出: Eb N = - E U0 U0是晶体在 0K 时的总能量,EN是N个自由粒子能量之和, 因此 Eb是0K时把晶体分解为相距无限远、静止的中性自由 原子所需要的能量,称作内聚能(Cohesive energy)或结 合能(binding energy)。取EN =0,做能量基点,则有: E U b = - 0

严格计算晶体总能量需要求解复杂的多粒子体系的定态薛 定锷方程,这是十分困难的。但我们可以近似把原子对间相互 作用能量之和当作晶体的总相互作用能。 物质以晶态存在是由于构成固体的原子之间存在着相当大 的相互作用力,尽管不同晶体这种结合力的类型和大小不同, 但两个粒子之间相互作用力(势)与它们间距离的关系在定性 上是相同的。 u(r) 晶体中粒子的相互作用 可以分为2大类:斥力 和引力。较大距离上引 斥力势 力为主,很接近时斥力 总相互作用势 为主,无限远处,相互 作用为零,晶态是粒子 间斥力、引力处于平衡 结合能 时的状态。 引力势
严格计算晶体总能量需要求解复杂的多粒子体系的定态薛 定锷方程,这是十分困难的。但我们可以近似把原子对间相互 作用能量之和当作晶体的总相互作用能。 物质以晶态存在是由于构成固体的原子之间存在着相当大 的相互作用力,尽管不同晶体这种结合力的类型和大小不同, 但两个粒子之间相互作用力(势)与它们间距离的关系在定性 上是相同的。 斥力势 引力势 u(r) r 晶体中粒子的相互作用 可以分为2大类:斥力 和引力。较大距离上引 力为主,很接近时斥力 为主,无限远处,相互 作用为零,晶态是粒子 间斥力、引力处于平衡 时的状态。 m r 总相互作用势 结 合 能
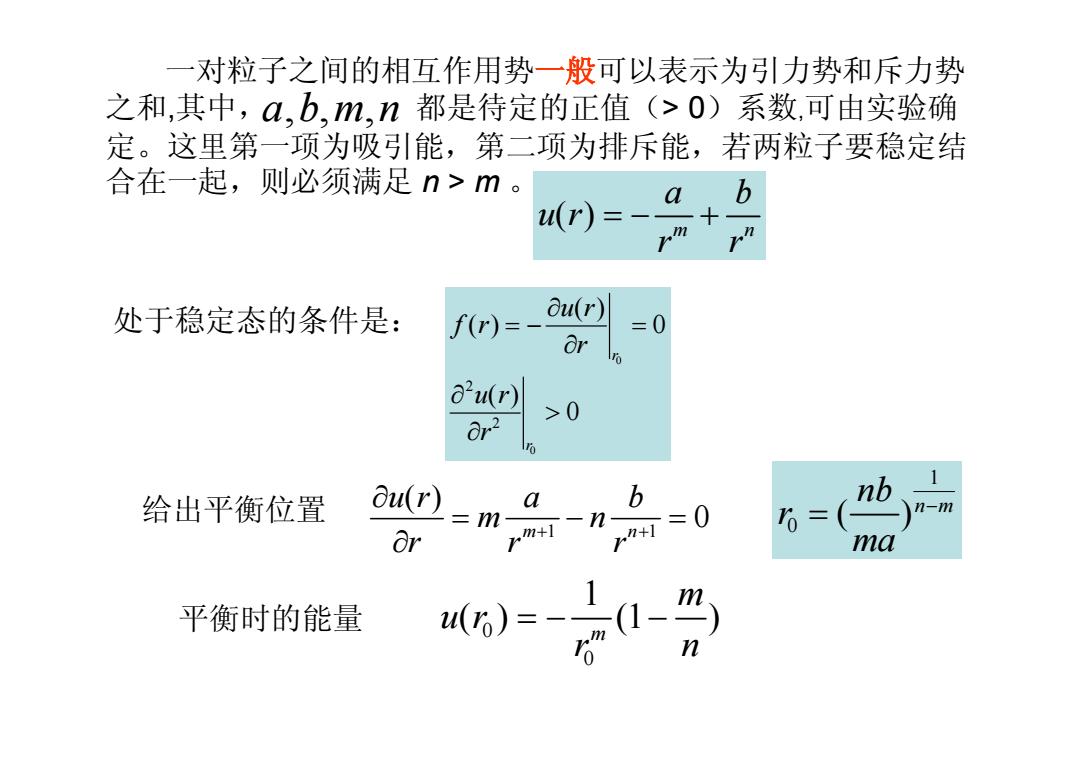
一对粒子之间的相互作用势一般可以表示为引力势和斥力势 之和,其中,a,b,m,n都是待定的正值(>0)系数,可由实验确 定。这里第一项为吸引能,第二项为排斥能,若两粒子要稳定结 合在一起,则必须满足n>m。 b (r)= rm 处于稳定态的条件是: f()=- ou(r) =0 Or a2u(r) 0r2 >0 au(r) a b nb、 给出平衡位置 =0 6=(2)n-m Or ma 平衡时的能量 )=1-2
一对粒子之间的相互作用势一般可以表示为引力势和斥力势 之和,其中, 都是待定的正值(> 0)系数,可由实验确 定。这里第一项为吸引能,第二项为排斥能,若两粒子要稳定结 合在一起,则必须满足 n > m 。 ( ) m n a b u r r r = - + 处于稳定态的条件是: 0 0 2 2 ( ) ( ) 0 ( ) 0 r r u r f r r u r r ¶ = - = ¶ ¶ > ¶ a,b, , m n 给出平衡位置 0 0 1 ( ) (1 ) m m u r r n 平衡时的能量 = - - 1 1 ( ) 0 m n u r a b m n r r r + + ¶ = - = ¶ 1 0 ( ) n m nb r ma - =

★从上式可以看出晶体有平衡态的条件是:n>m ★更符合实际斥力势变化规律的表达式为指数形式: be N个原子组成晶体后的总相互作用能,忽略边界的差异,可 以近似表示为: U)∑24,)24,) 严格说,晶体作为一个封闭系统的内能应包括: a.(上面给出的)晶格相互作用能UV),它是体积的函数。 b.晶格振动能U(T,),T≠OK时能量的增加。 C.零点能,这是量子效应。 d.晶格缺陷能。 本章只限于考虑晶格能,第3、4两章再分别讨论2、4两项,以 后还将考虑:电子气能量,磁自旋波能量等
★从上式可以看出晶体有平衡态的条件是:n > m ★更符合实际斥力势变化规律的表达式为指数形式: r be a - N个原子组成晶体后的总相互作用能,忽略边界的差异,可 以近似表示为: 1 1 1 1 ( ) ( ) ( ) 2 2 N N N ij ij i i i j i i N U r u r u r ¹ ¹ = åå å B 严格说,晶体作为一个封闭系统的内能应包括: a.(上面给出的)晶格相互作用能U(V),它是体积的函数。 b. 晶格振动能U(T,V),T≠0K 时能量的增加。 c. 零点能,这是量子效应。 d. 晶格缺陷能。…… 本章只限于考虑晶格能,第3、4两章再分别讨论2、4两项,以 后还将考虑:电子气能量,磁自旋波能量等