
4.3金属的热容和顺磁磁化率 一自由电子的热容 二.自由电子的顺磁磁化率 参考:黄昆书p282-286,p395-399 Kittel8版6.4节:11.6节 4.1节中提到:室温下几乎观测不到经典理论预言的自 由电子对热容的贡献,因此索末菲自由电子理论能否正确地 解释金属热容和顺磁磁化率随温度的变化关系,克服经典电 子论的这个困难是它是否成功的考验。 其实从4.2节的描述中已经定性地看到了结果,自由电子 服从费米-狄拉克分布,只有位于费米面附近的少数电子才能 受到kT的热激发,对热容有贡献,其它大部分电子是不能 被激发参与热容贡献的,这就改正了经典理论全部电子都参 与贡献的错误判断
4.3 金属的热容和顺磁磁化率 一. 自由电子的热容 二. 自由电子的顺磁磁化率 参考:黄昆 书p282-286,p395-399 Kittel 8版6.4节;11.6节 4.1 节中提到:室温下几乎观测不到经典理论预言的自 由电子对热容的贡献,因此索末菲自由电子理论能否正确地 解释金属热容和顺磁磁化率随温度的变化关系,克服经典电 子论的这个困难是它是否成功的考验。 其实从4.2节的描述中已经定性地看到了结果,自由电子 服从费米-狄拉克分布,只有位于费米面附近的少数电子才能 受到 kBT 的热激发,对热容有贡献,其它大部分电子是不能 被激发参与热容贡献的,这就改正了经典理论全部电子都参 与贡献的错误判断

一.电子热容量: 4.2中我们曾讨论了T>0K时电子的分布,此时的能量为: (E(E-cEC 仍利用分部积分和函数E)的特点求解,可得: 由于正常情况下E>kT 所以能量随温度的增加很小。 平均到每个电子的能量为: 门
一. 电子热容量: 4.2 中我们曾讨论了T>0K时电子的分布,此时的能量为: ' 3 5 2 2 0 0 0 2 ( ) ( )d ( )d ( )d 5 U Ef E N E E C E f E E CE f E E ¥ ¥ ¥ æ ö = = = ç ÷ è ø ò ò ò 仍利用分部积分和函数 f(E) 的特点求解,可得: 2 2 0 0 5 1 12 B F k T U U E p é ù æ ö = + ê ú ç ÷ ê ú è ø ë û 由于正常情况下 所以能量随温度的增加很小。 0 EF B >> k T 平均到每个电子的能量为: 2 2 2 0 2 0 0 0 5 3 5 1 1 12 5 12 B B F F F k T k T u u E E E p p é ù é ù æ ö æ ö = ê + ú = + ê ú ç ÷ ç ÷ ê è ø ú ê ú è ø ë û ë û

自由电子系统的克分子热容为: C。=N4 - 即便是在较高温度下,T<<TE,所以:Ce<Cy ~1% 但在极低温度下,晶格热容下降很快,电子热容反而会 显著起来。 =bT3 (见3.3节) C。=yT 所以极低温度下,应有: C=C。+Cv=yT+bT3 实验完全证实了这个关系,测出的Y和b值都成了 标识材料性质的量
自由电子系统的克分子热容为: 2 2 0 2 2 B e A A B A B V F F u k T T C N N k N k T E T æ ö ¶ p p æ ö æ ö = ç ÷ = = ç ÷ ç ÷ è ø ¶ è ø è ø 即便是在较高温度下,T<<TF,所以:Ce <<CV。 但在极低温度下,晶格热容下降很快,电子热容反而会 显著起来。 3 12 4 3 5 V A B D T C N k bT T p æ ö = = ç ÷ è ø C T e = g 所以极低温度下,应有: 3 C = Ce V + C = + gT bT 实验完全证实了这个关系,测出的 和 b 值都成了 标识材料性质的量。 g : 1% (见3.3节)
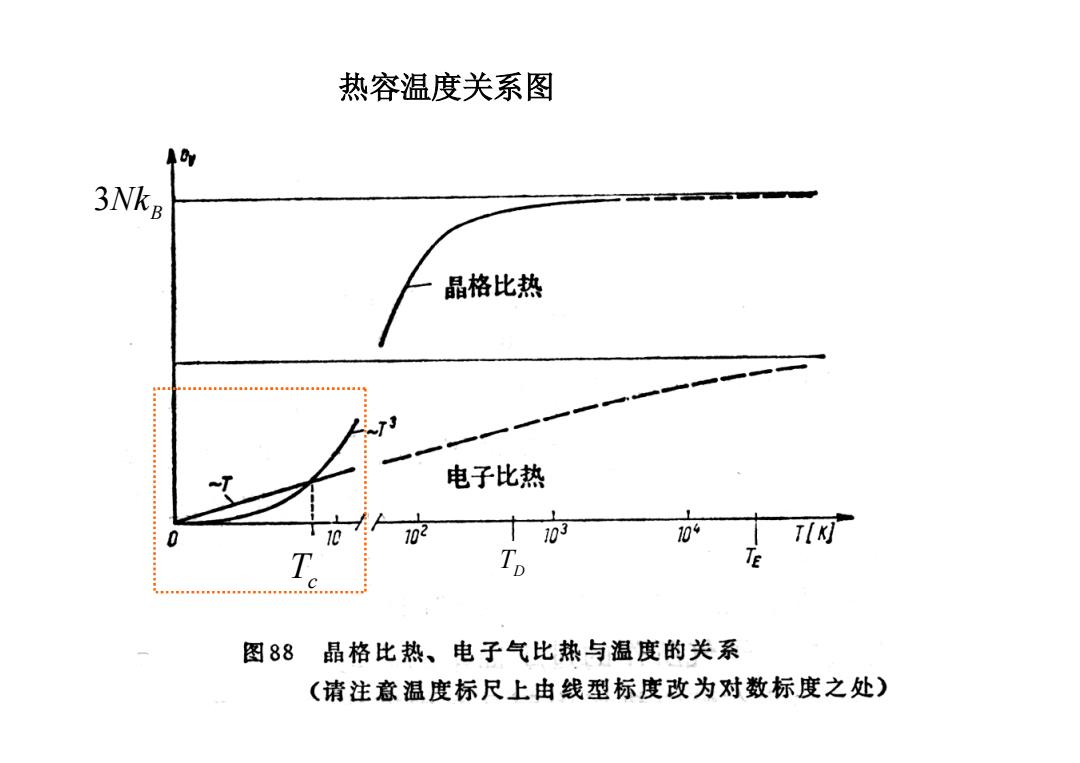
热容温度关系图 3Nkg 晶格比热 电子比热 102 03 10 T[K] T T 图88晶格比热、电子气比热与温度的关系 (请注意温度标尺上由线型标度改为对数标度之处)
热容温度关系图 3NkB TD T c

金属极低温下热容的变化曲线:存在一个临界温度,此温度 以下,电子热容反而变得比 晶格热容更大些。 当Ce=Cv时,有: 号wk (C。+C) 可确定出此时的温度: 1.2 78 4元2TE 对于简单金属,TD~102K, TF~104K,估算出Tc~1K的 数量级。所以,在很低温度 下,电子热容量与晶格热容量 Temperature (kelvins) 同数量级,这时,电子热容量 见:Blakemore书p179 就不可忽略
金属极低温下热容的变化曲线:存在一个临界温度,此温度 以下,电子热容反而变得比 晶格热容更大些。 当Ce=CV时,有: 3 2 12 4 5 2 A B A B D F T T N k N k T T p p æ ö æ ö ç ÷ = ç ÷ è ø è ø 可确定出此时的温度: 3 2 5 24 D c F T T p T = 见:Blakemore 书p179 对于简单金属, TD ~ 102 K, TF ~ 104 K,估算出TC ~ 1 K的 数量级。所以,在很低温度 下,电子热容量与晶格热容量 同数量级,这时,电子热容量 就不可忽略