
5.5克勒尼希-彭尼(Kronig-Penny)模型: 我们从近自由电子近似(NFE)和紧束缚近似(TB) 两种极端情形下的讨论中得出了共同的结论,即:晶体中 电子的能级形成允带和禁带,但为了能和实际晶体的实验 结果相比较,使用尽可能符合晶体实际情况的周期势,求解 具体Schrodinger方程的尝试从没有停止过,最早的一个 模型是1931年Kronig-Penney一维方形势场模型,它可 以用简单的解析函数严格求解,也得出了周期场中运动的 粒子允许能级形成能带,能带之间是禁带的结论,但这是 一维周期势场,还不能算是真正的尝试。不过近来却常使 用Kronig-Penney势讨论超晶格的能带。 见: Kittel8版7.3节p119:7.4.4节p124 方俊鑫书5.6节p204; 冯端《凝聚态物理学》5.2.4节p150
我们从近自由电子近似(NFE)和紧束缚近似(TB) 两种极端情形下的讨论中得出了共同的结论,即:晶体中 电子的能级形成允带和禁带,但为了能和实际晶体的实验 结果相比较,使用尽可能符合晶体实际情况的周期势,求解 具体 Schrodinger 方程的尝试从没有停止过,最早的一个 模型是 1931年 Kronig-Penney 一维方形势场模型,它可 以用简单的解析函数严格求解,也得出了周期场中运动的 粒子允许能级形成能带,能带之间是禁带的结论,但这是 一维周期势场,还不能算是真正的尝试。不过近来却常使 用 Kronig-Penney 势讨论超晶格的能带。 5.5 克勒尼希-彭尼(Kronig-Penny) 模型: 见: Kittel 8版 7.3节 p119;7.4.4节p124 方俊鑫 书5.6节 p204; 冯端《凝聚态物理学》5.2.4节p150
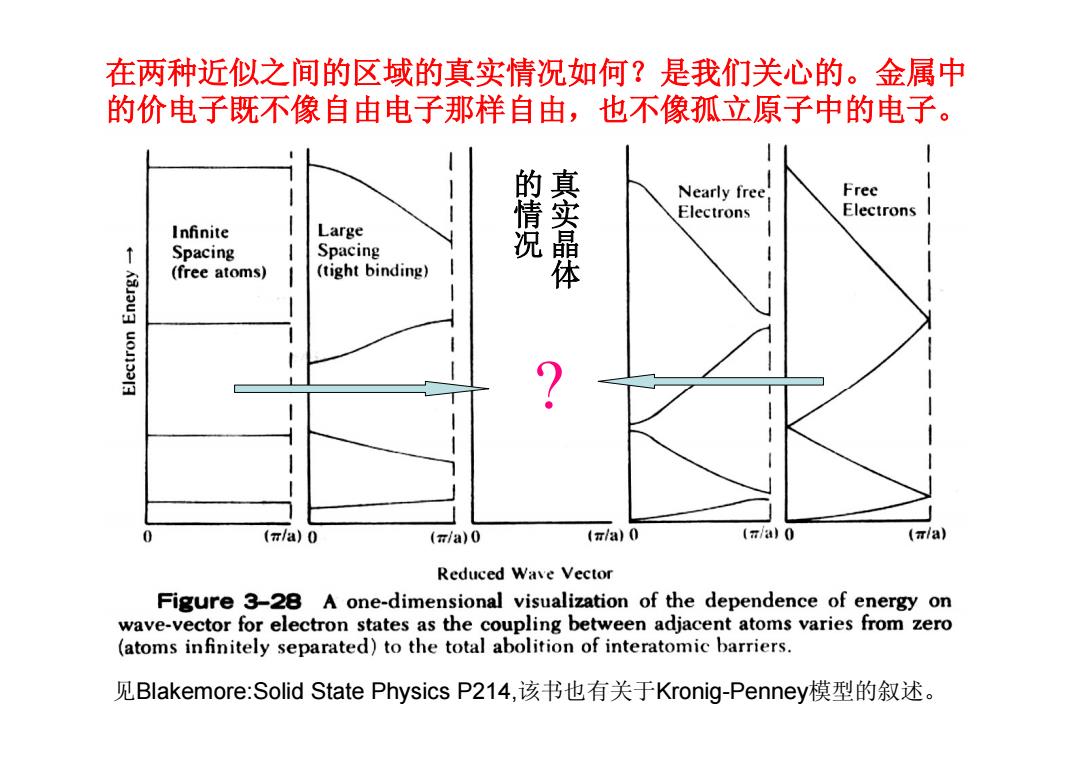
在两种近似之间的区域的真实情况如何?是我们关心的。金属中 的价电子既不像自由电子那样自由,也不像孤立原子中的电子。 的情况 真实晶体 Nearly free Free Electrons Electrons Infinite Large Spacing Spacing (free atoms) (tight binding) (r/a)0 (m/a)0 (z/a)0 (n/a)0 (mia) Reduced Wave Vector Figure 3-28 A one-dimensional visualization of the dependence of energy on wave-vector for electron states as the coupling between adjacent atoms varies from zero (atoms infinitely separated)to the total abolition of interatomic barriers. 见Blakemore:Solid State Physics P214,该书也有关于Kronig-Penney模型的叙述
在两种近似之间的区域的真实情况如何?是我们关心的。金属中 的价电子既不像自由电子那样自由,也不像孤立原子中的电子。 ? 真 实 晶 体 的 情 况 见Blakemore:Solid State Physics P214,该书也有关于Kronig-Penney模型的叙述
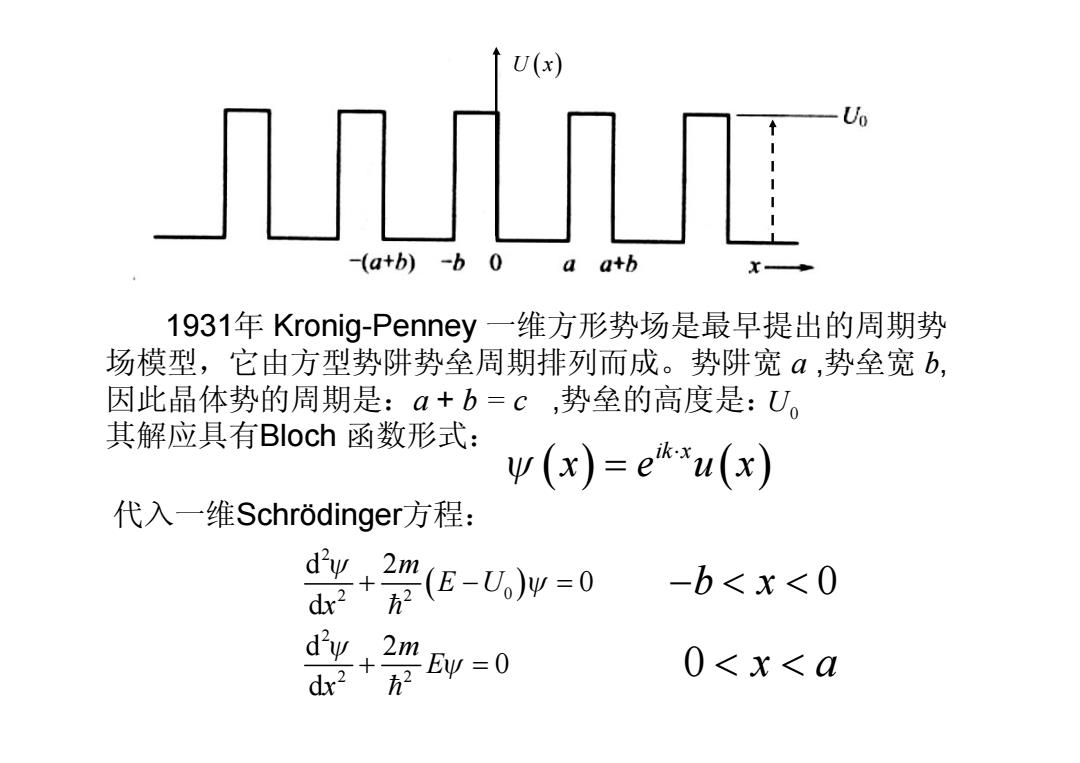
U(x) Uo -(a+b)-b 0 aa+b x 1931年Kronig-Penney一维方形势场是最早提出的周期势 场模型,它由方型势阱势垒周期排列而成。势阱宽α,势垒宽b, 因此晶体势的周期是:a+b=c,势垒的高度是:U。 其解应具有Bloch函数形式: w(x)=eu(x) 代入一维Schrodinger方程: +(5-w=0 d2 -b≤x<0 dx2 dw .3 dx2 2m Ew =0 2 0<x<a
1931年 Kronig-Penney 一维方形势场是最早提出的周期势 场模型,它由方型势阱势垒周期排列而成。势阱宽 a ,势垒宽 b, 因此晶体势的周期是:a + b = c ,势垒的高度是: 其解应具有Bloch 函数形式: U x( ) U0 ( ) ( ) ik x y x e u x × = 代入一维Schrödinger方程: ( ) 2 2 2 0 2 2 2 d 2 0 d d 2 0 d m E U x m E x y y y y + - = + = h h -b x < < 0 0 < < x a

1.在区域0<x<a:U,=0 2e+[-)-0 dx2 dx 令: 2mE = h2 +2a-a0 dx2 这是一个二阶常系数微分方程,它的解为: u(x)=Aea-k)*+Be-iatk) w(x)=Aeiax+Be-icx 其中A,B都是任意常数。这个区域内的本征函数是向右 和向左行进的平面波的线性组合。而能量: E= h2a2 2m
1. 在区域 0 < < x a : 0 U = 0 ( ) ( ) ( ) 2 2 2 2 d d 2 2 0 d d u x u x m ik E k u x x x é ù + + - = ê ú ë û h 令: 2 2 2mE = a h ( ) ( ) ( ) 2 2 2 2 d d 2 0 d d u x u x ik k u x x x + + é ù a - = ë û 这是一个二阶常系数微分方程,它的解为: ( ) i( k )x i( k x) u x Ae Be a a - - + = + 其中A,B都是任意常数。这个区域内的本征函数是向右 和向左行进的平面波的线性组合。而能量: 2 2 2 E m a = h ( ) i x i x x Ae Be a a y × - × = +

2.在区域:-b<x<0 tem+-)o0 dx2 E<Uo g--)-2m心- -2a-[g]a(=o dx2 其解: u(x)=Ce(-)+De-(+) 所以有: w(x)=Ceax+De-Bx 同样C,D都是任意常数。 U。-E= h2B2 2m
2. 在区域: -b x < < 0 ( ) ( ) ( ) ( ) 2 2 2 2 0 d d 2 2 0 d d u x u x m ik E U k u x x x é ù + + - - = ê ú ë û h ( ) 2 2 0 2 2 0 2 2 m mU b a = U E - = - h h E U< 0 ( ) ( ) ( ) 2 2 2 2 d d 2 0 d d u x u x ik k u x x x + - é ù b + = ë û 其解: ( ) ( ik )x ( ik x) u x Ce De b b - - + = + 同样C,D都是任意常数。 ( ) x x x Ce De b b y - = + 2 2 0 2 U E m b - = h 所以有: