一.一维单原子链的振动 运动方程: 考虑N个质量为m的同种原子组成的一维单原子链的。设 平衡时相邻原子间距为a(即原胞大小),在t时刻第n个原 子偏离其平衡位置的位移为n (+1)a (n+2)a &微880m0om0 1(n-2)a }(n-1)a 装匹 Un_2 un un+2
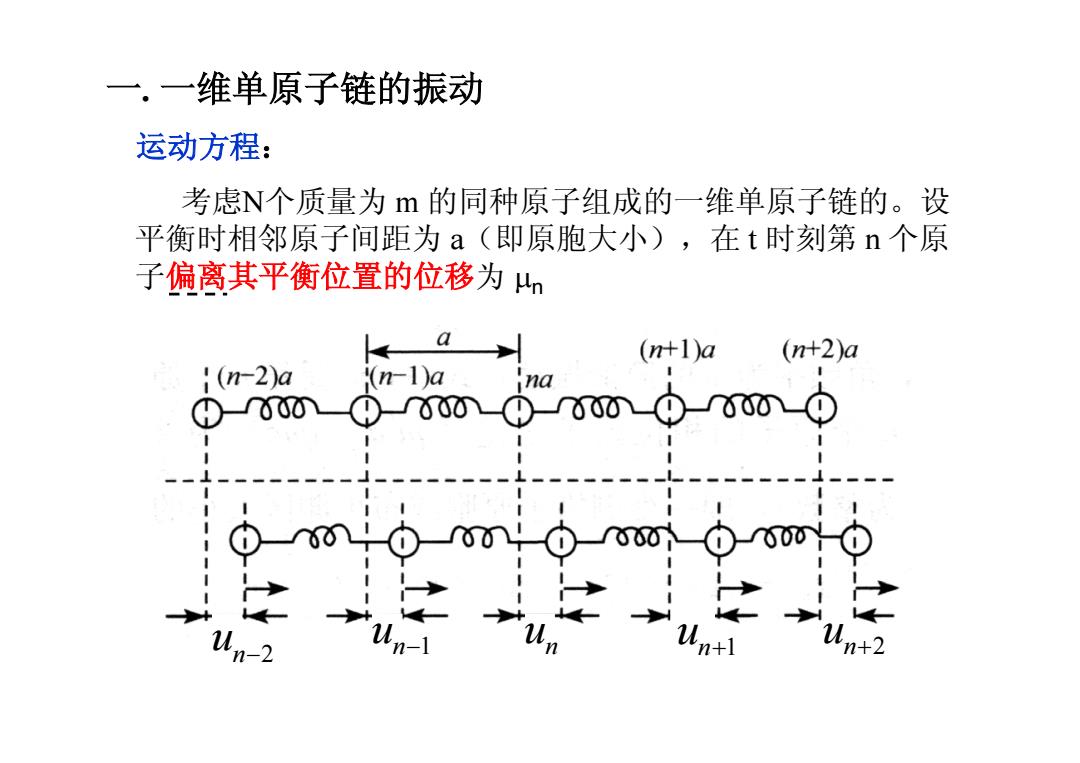
一. 一维单原子链的振动 运动方程: 考虑N个质量为 m 的同种原子组成的一维单原子链的。设 平衡时相邻原子间距为 a(即原胞大小),在 t 时刻第 n 个原 子偏离其平衡位置的位移为 mn n u n 1 u + n 2 u n 1 + u - n 2 u -

为了建立起运动方程,我们首先要对原子之间的相互作用力 做些讨论,设在平衡时,两原子的相互作用势为V(),产生 相对位移(例如δ=u1-w,)后势能发生变化是V(a+δ), 将它在平衡位置附近做泰勒展开: 首项是常数,可取为能量零点,由于平衡时势能取极小值,第 二项为零,简谐近似下,我们只取到第三项,即势能展开式 中的二阶项(δ项),而忽略三阶及三阶以上的项,显然, 这只适用于微振动,即δ值很小的情况。此时,恢复力: 6=-β6 相当于把相邻原子间的相互作用力看 dr dr2 作是正比于相对位移的弹性恢复力。 d"V B称为恢复力常数 B=
为了建立起运动方程,我们首先要对原子之间的相互作用力 做些讨论,设在平衡时,两原子的相互作用势为V(a),产生 相对位移(例如 )后势能发生变化是V(a+δ) , 将它在平衡位置附近做泰勒展开: n n 1 d u u = - + 2 3 2 3 2 3 d 1 d 1 d ( ) ( ) ( ) d a 2 d 3! d a a V V V V r V a V a r r r d d d d æ ö æ ö æ ö = + = + + + + ××× ç ÷ ç ÷ ç ÷ è ø è ø è ø 首项是常数,可取为能量零点,由于平衡时势能取极小值,第 二项为零,简谐近似下,我们只取到第三项,即势能展开式 中的二阶项(δ2项),而忽略三阶及三阶以上的项,显然, 这只适用于微振动,即δ值很小的情况。此时,恢复力: 2 2 d d d d a V V f r r d bd æ ö = - = -ç ÷ = - è ø β称为恢复力常数 2 2 d d a V r b æ ö = -ç ÷ è ø 相当于把相邻原子间的相互作用力看 作是正比于相对位移的弹性恢复力

如只考虑最近邻原子间的相互作用,第n个原子受到的力: fn=f+2=-B(4n-4n+1)-B(4n-4n-1)=B(un+1+4n-1-24n)) 于是第n个原子的运动方程可写为: m d=B(4+4-24,) 一 维原子链上的每个原子,忽略边界原子的区别,应 有同样的方程,所以它是和原子数目相同的N个联立的线 性齐次方程。 方程的解:这样的线性齐次方程应有一个波形式的解: Hng Aei(ol-nag) 2元 λ A是振幅,w是角频率,q是波数,入是波长,naq是第n 个原子的位相因子,将试解代入方程求解
( ) ( ) ( ) f n = f f 1 + 2 = -b mn - mn+1 - b mn - mn-1 = b mn+ - 1 1 + - m m n n 2 如只考虑最近邻原子间的相互作用,第 n 个原子受到的力: ( ) 2 2 1 1 d 2 d n n n n u m t = b m + - + - m m 于是第n个原子的运动方程可写为: 一维原子链上的每个原子,忽略边界原子的区别,应 有同样的方程,所以它是和原子数目相同的 N个联立的线 性齐次方程。 方程的解:这样的线性齐次方程应有一个波形式的解: ( ) nq i t naq Ae w m - = A是振幅,ω是角频率,q 是波数,λ是波长,naq 是第n 个原子的位相因子,将试解代入方程求解。 2 q p l =

-mw'Ae-l=BhAeor-ao+Aeao-网-2ieeun -mo2=B(e-iag +eiag-2)=2B(cosaq-1) (利用欧拉公式) 色散关系 解得 -ag m Dispersion curves 这里⊙可正可负,我们取正值。丢掉了虚数解,因为晶体稳定 性要求o2≥0,否则原子位移将随时间增长而趋于无穷。 这个结果与无关,说明N个方程都有同样结果,即所有原 子都同时以相同的频率。和相同的振幅A在振动,但不同的 原子间有一个相差,相邻原子间的相差是ga 该结果还表示:只要⊙和q满足上述关系,试解就是联立方 程的解。通常把⊙和q的关系称作色散关系
这里ω可正可负,我们取正值。丢掉了虚数解,因为晶体稳定 性要求ω2≥0,否则原子位移将随时间增长而趋于无穷。 这个结果与 n 无关,说明 N 个方程都有同样结果,即所有原 子都同时以相同的频率ω和相同的振幅 A 在振动,但不同的 原子间有一个相差,相邻原子间的相差是 。 该结果还表示:只要ω和q 满足上述关系,试解就是联立方 程的解。通常把ω和 q 的关系称作色散关系。 ( ) ( ) ( ) ( ) { } 2 1 1 2 i t naq i t n aq i t n aq i t naq m Ae Ae Ae Ae w w w w w b é ù é ù ë û ë û - - - + - - - = + - ( ) ( ) 2 2 2 cos 1 iaq iaq mw b b e e aq - - = + - = - 1 2 sin 2 aq m b 解得 w = —— 色散关系 Dispersion curves qa (利用欧拉公式)

解的物理意义:格波 Aei(ot-nag) 原子振动以波的方式在晶体中传播。当两原子相距 2x 的 整数倍时,两原子具有相同的振幅和位相。 如:ma=na+2π1,m,n.l都是整数) 有:wn=Aexp[i(ot-mag)]=Aexp[i(ot-nag)]exp(-i2πl) Aexp i(ot-naq)=u, ≥1 该解表明:晶体中所有原子共同 参与的振动,以波的形式在整个 ↑】 n+2 晶体中传播,称为格波。 从形式上看,格波与连续介质弹性波完全类似,但连续介质 弹性波中的x是可以连续取值的;而在格波中只能取na格点位 置这样的孤立值。 连续介质弹性波:Ae(o-q)
解的物理意义: 格波 原子振动以波的方式在晶体中传播。当两原子相距 的 整数倍时,两原子具有相同的振幅和位相。 2 ma na l,(m, , n l q p = + 都是整数)。 2 q p 如: ( ) ( ) ( ) exp exp exp( 2 ) exp m n u A i t maq A i t naq i l A i t naq u w w p w = é - ù = é ù - - ë û ë û = é ù - = ë û 有: = 1 该解表明:晶体中所有原子共同 参与的振动,以波的形式在整个 晶体中传播,称为格波。 从形式上看,格波与连续介质弹性波完全类似,但连续介质 弹性波中的 x 是可以连续取值的;而在格波中只能取 na 格点位 置这样的孤立值。 ( ) nq i t naq Ae w m - = ( ) A i t xq e 连续介质弹性波: w -