
2极坐标系 某些平面图形,用极坐标来计算是比较方便的 若曲线由极坐标方程r=r(8),(≤0≤)给出 极坐标系下研究面积的基本图形不是曲边梯形 而是由射线0=与8=B甲辩=(日) 所围成的称为曲边扇形的区域 由于曲边扇形的面积分布与有关 当d很小时r()的变化不大 △A可用半径为r(8)圆心角为d0
2 极坐标系 某些平面图形,用极坐标来计算是比较方便的 若曲线由极坐标方程 r = r( ),( ) 给出 极坐标系下研究面积的基本图形不是曲边梯形 而是由射线 = 与 = 及曲线r = r( ) 所围成的称为曲边扇形的区域 与有关 当d很小时 r( )的变化不大 A 可用半径为 r( ) 圆心角为 d 由于曲边扇形的面积分布
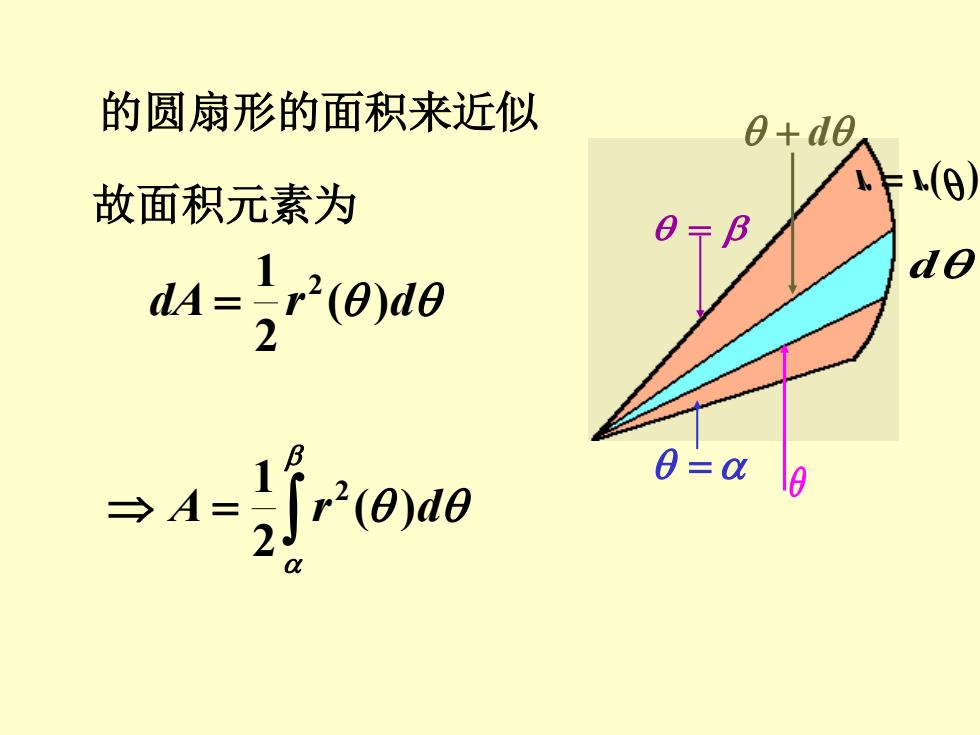
的圆扇形的面积来近似 +do 故面积元素为 (0 AOo do =0 18
故面积元素为 = A r ( )d 2 1 2 dA r ( )d 2 1 2 = = = + d d r = r( ) 的圆扇形的面积来近似
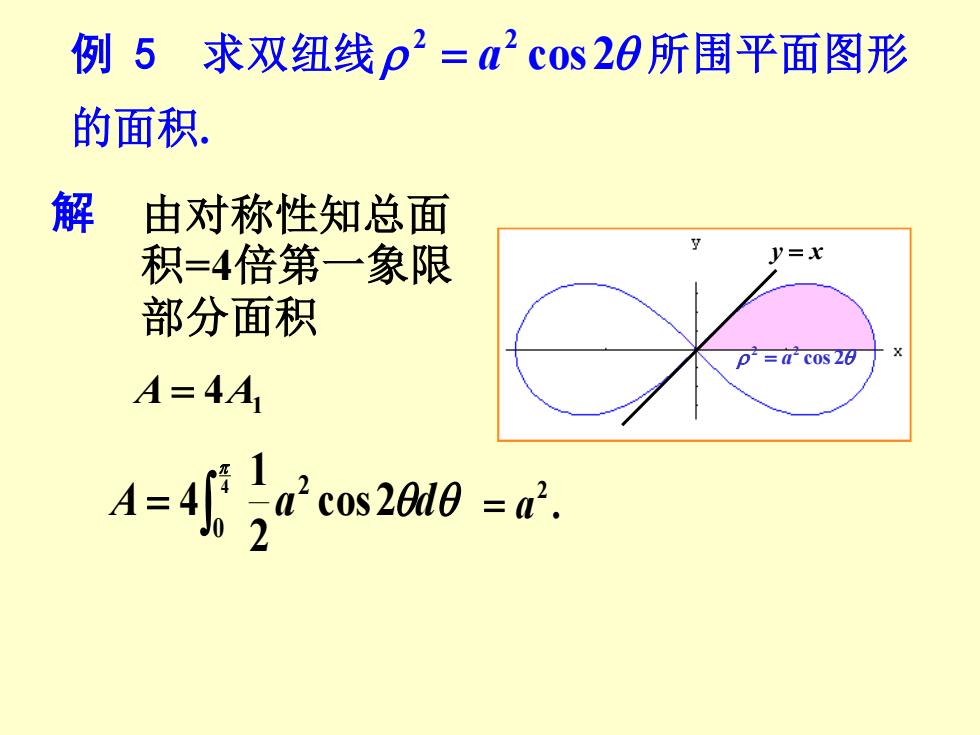
例5求双纽线p2=2c0s20所围平面图形 的面积. 解 由对称性知总面 积=4倍第一象限 P=x 部分面积 p=心c0s20 A=4A1 a"cos20d0 a
例 5 求双纽线 cos 2 2 2 = a 所围平面图形 的面积. 解 由对称性知总面 积=4倍第一象限 部分面积 A = 4A1 A a cos 2 d 2 1 4 4 0 2 = . 2 = a cos 2 2 2 = a y = x