
自动控制理论 零阶保持器(ZOH)是把kT时刻的采样值恒值地保持到下一采样时 刻(K+1)T。 由图7-13(b)得 脉冲响应 8h(t)=1(t)-1(t-T) 传递函数 C,(S)=1-ew S 频率特性 G(j@)=1-e- sin(OT =TO e jo 把T=2” 2 代入上式,得 G,(j@)= 2 sin(@o) -e @s π0 /0s 16 第七章离散控制系统 2025/1/14
ZOH 16 第七章 离散控制系统 2025/1/14 零阶保持器( )是把kT时刻的采样值恒值地保持到下一采样时 刻(K+1)T。 由图7-13(b)得 脉冲响应 传递函数 频率特性 g (t) l(t) l(t T) h = − − S e G S TS h − − = 1 ( ) 2 2 ) 2 sin( 1 ( ) j T Tj h e T T T j e G j − − = − = S T 2 = ( ) sin( ) 2 ( ) S j S h S S G j e − = 把 代入上式,得 自动控制理论
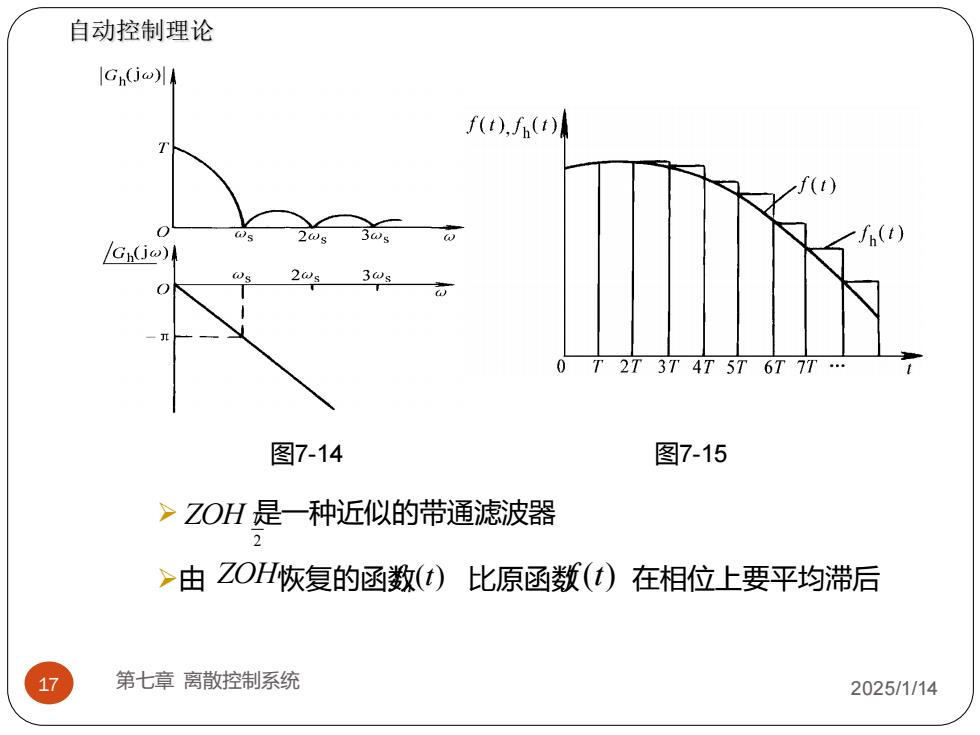
自动控制理论 Gh(j) f(),f() Gh(j) 27T 3T 4T 5T 6T 7T 图7-14 图7-15 >ZOH是一种近似的带通滤波器 >由ZOH恢复的函数(t)比原函数(t)在相位上要平均滞后 17 第七章离散控制系统 2025/1/14
ZOH f (t) h 2 ZOH T 17 第七章 离散控制系统 2025/1/14 图7-14 图7-15 ➢ 是一种近似的带通滤波器 ➢由 恢复的函数 比原函数 f (t) 在相位上要平均滞后 自动控制理论

自动控制理论 第三节Z变换与Z反变换 一、Z变换 设离散化信号 f(->f(T)6u-KT) k=0 F^(s)=[f(】=∑fkT)es 令Z=es,则 ()=( L- 定义: F(e)=Zf(=∑fkT): Z变换的三种求法: 18 第七章离散控制系统 2025/1/14
第三节 Z变换与Z反变换 18 第七章 离散控制系统 2025/1/14 一、Z变换 设离散化信号 * 0 ( ) ( ) ( ) k f t f kT t kT = = − = − = = 0 * * ( ) [ ( )] ( ) k kTS F s L f t f k T e TS Z = e = − = = = 0 l n 1 * ( ) ( ) ( ) k k z T s F z F s f k T z = − = = 0 * ( ) [ ( )] ( ) k k F z Z f t f k T z 令 ,则 定义: Z变换的三种求法: 自动控制理论

自动控制理论 1、级数求和法 例7-1求:Z1(t)] 解: 当k≥0时,f(kT)=1,则有 F(e)=Z[]=∑=1+21+z2+ k=0 如果<1,则上式可写为: F(z)=, 例7-2求:ZIe],a>0 解:f(e)-e:*-1+e:+erg3+ k-0 如果ez<1,则: F(e)-1-o 19 第七章离散控制系统 2025/1/14
z 1 1 1 1 ( ) 1 − = − = − z z z F z a T a T z e z e z F z − − − − = − = 1 1 1 ( ) 19 第七章 离散控制系统 2025/1/14 Z t [1( )] k 0 f (kT) =1 1 2 0 ( ) [1( )] 1 . k k F z Z t z z z − − − = = = = + + + 解: 例7-1 求: 1、级数求和法 当 时, ,则有 如果 ,则上式可写为: [ ] at Z e − a 0 1 1 − − e z aT ( ) 1 . 1 2 2 0 = = + + + − − − − = − − F z e z e z e z a T a T k akT k 例7-2 求: , 解: 如果 ,则: 自动控制理论

自动控制理论 2、部分分式法 a 例7-3求的F(s)= 的Z变换 s(s+a) 解: FS)=11 ss+a f(t)=1-e-aT 1 1 (1-e-aT)=1 Fe)=Zf]=1-1-e21-2X1-e 例7-4求 Z(sna)-1 解: -212 F(s)s+jas-jd F(2)= 1-earz-T1-earz- (sin aT)z 1-(2cosaT)z+-2 20 第七章离散控制系统 2025/1/14
20 第七章 离散控制系统 2025/1/14 ( ) ( ) s s a a F s + = 2、部分分式法 例7-3 求的 的Z变换 解: (1 )(1 ) (1 ) 1 1 1 1 ( ) [ ( )] 1 1 1 1 1 − − − − − − − − − − − = − − − = = z e z e z z e z F z Z f t aT aT aT aT f t e − ( ) =1− s s a F s + = − 1 1 ( ) Z(sin at) s j a j s j a j s a a F s − + + − = + = 2 1 2 1 ( ) 2 2 1 2 1 1 1 1 (2cos ) (sin ) 1 2 1 1 2 1 ( ) − − − − − − − + = − + − − = aT z z aT z e z j e z j F z jaT jaT 例7-4 求 解: 自动控制理论