
(4)不可逆相变过程的相变熵 可逆相变一定是在恒温恒压下进行的,但并不意味凡是恒 温恒压下进行的相变都是可逆相变。例如101.325kPa、90℃的水 蒸气在恒温恒压下变成同温同压的液体水,此过程就不是可逆 相变。凡不是在无限接近相平衡条件下进行的相变过程,均为 不可逆相变过程。因此,在求取不可逆相变过程的△相变S时,不 能用不可逆相变过程中系统与环境交换的热Q除以过程温度T来 计算。不可逆相变过程的△相变S的计算是通过在相同的始末态间 设计一可逆过程,然后计算此可逆过程熵变△相变S,由于始末态 确定后,状态函数熵的变化值△相变S与过程无关,故由可逆过程 求得的△相变S也就是不可逆相变过程的△相变S。 例5-1-4计算101.325kPa、50℃的1molH0(1)变成101.325kPa、 50℃的1molH2Og)的△amS。已知水的C2m(1)=73.5J-K-1.mol-1, Cpm(g)=33.6J-K-.mol-,100C时的△aHnm=40.59 kJ-mol'-
(4)不可逆相变过程的相变熵 可逆相变一定是在恒温恒压下进行的,但并不意味凡是恒 温恒压下进行的相变都是可逆相变。例如101.325kPa、90℃的水 蒸气在恒温恒压下变成同温同压的液体水,此过程就不是可逆 相变。凡不是在无限接近相平衡条件下进行的相变过程,均为 不可逆相变过程。因此,在求取不可逆相变过程的△相变S时,不 能用不可逆相变过程中系统与环境交换的热 Q 除以过程温度T来 计算。不可逆相变过程的△相变S的计算是通过在相同的始末态间 设计一可逆过程,然后计算此可逆过程熵变△相变S,由于始末态 确定后,状态函数熵的变化值△相变S与过程无关,故由可逆过程 求得的△相变S也就是不可逆相变过程的△相变S。 例5-1-4 计算101.325kPa、50℃的1molH2O(1)变成101.325kPa、 50℃的1molH2O(g)的△vapS。已知水的Cp.m(1) =73.5J·K-1·mol-1, Cp,m(g) =33.6J·K-1·mol-1,100℃时的△vapHm= 40.59kJ·mol-1

解:这是一不可逆相变过程,△pS不能直接求取,需要始末态 之间设计一可逆过程。可逆过程如何设计,应取决于题目给出 的数据。如本题给了水在100℃、101.325kPa的摩尔蒸发焓,为 此可设计出如下的可逆途径。 H20(1) T2=323.15K T,P H20(1) T2=323.15K 1mol P2101.325kPa △相S2 1mol P2101.325kPa P △S p △S H20(1) T1=373.15K T H20(1) T1=373.15K 1mol P1=101.325kPa △相1 1mol P1-101.325kPa 因此△S2=△S1+△和S1+△S A心-月2Cuor-CH,o T
解:这是一不可逆相变过程,△vap S不能直接求取,需要始末态 之间设计一可逆过程。可逆过程如何设计,应取决于题目给出 的数据。如本题给了水在100℃、101.325kPa的摩尔蒸发焓,为 此可设计出如下的可逆途径。 H 2O ( l ) T2 = 323.15K 1mol p 2=101.325kPa H 2O ( l ) T2 = 323.15K 1mol p 2=101.325kPa H 2O ( l ) T1 = 373.15K 1mol p 1=101.325kPa H 2O ( l ) T1 = 373.15K 1mol p 1=101.325kPa T , p △ 相 S2 T , p △ 相 S 1 p △ S 1 p △ S3 因此 △ 相 S2 = △ S1+ △ 相 S1+ △ S3 2 1 , 2 , 2 1 ( H O,1 )ln ( H O,1 ) 1 2 T T dT nC T nC S p m T T p m ∆ = = ∫
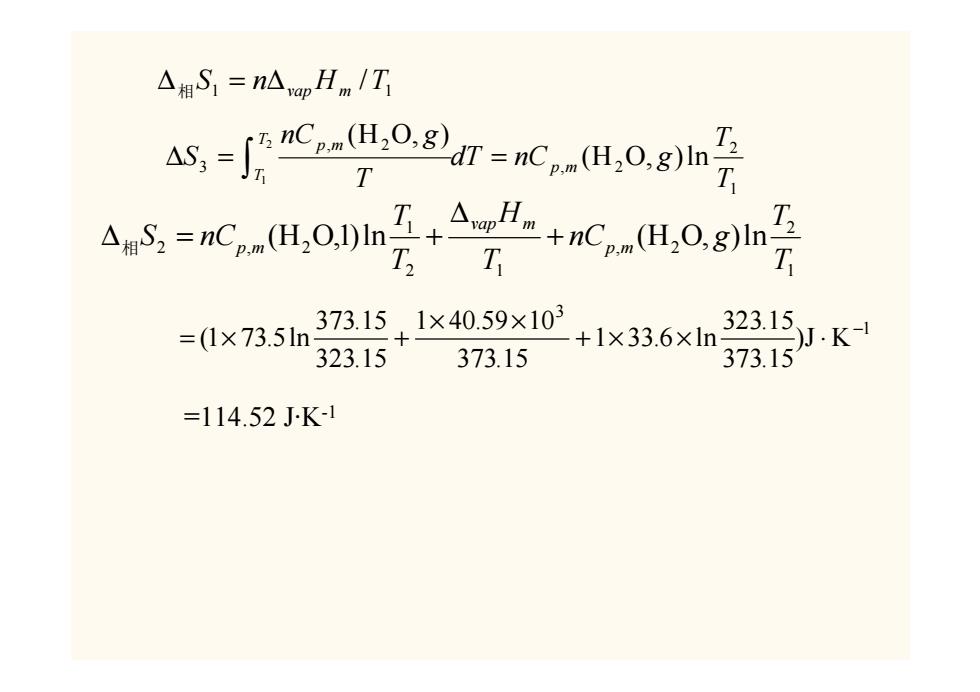
△相S1=nAyap Hm/T A,-C-H0副r=Kom,0gn2 T dS,=nC,H0h2+△≥-+nC,(H,0g T 373.15.x4059×10+1×33.6xn 323.15 =(1×73.5ln )J.K- 323.15 373.15 373.15 =114.52JK-1
1 2 , 2 , 2 3 (H O, )ln (H O, ) 2 1 T T dT nC g T nC g S p m TT p m ∆ = = ∫ 1 1 ∆相S = n∆vapHm /T 1 2 , 2 2 1 1 2 , 2 (H O,1)ln (H O, )ln TT nC g TH TT S nC p m vap m p m + ∆ ∆相 = + 1 3 )J K 373.15 323.15 1 33.6 ln 373.15 1 40.59 10 323.15 373.15 (1 73.5ln − + × × ⋅ × × = × + =114.52 J·K-1

4相变过程自发性判据 为了判断一个在指定条件下进行的相变过程能否自发进 行, 需要热力学判据。这样的判据有两个,一个是把系统和环境看 成是一个孤立系统,分别计算出系统和环境的熵变后,应用孤 立系统的熵变作为判据来判断过程的自发性。另一个是分别计 算出系统的焓变和熵变后,再计算系统的吉布斯函数增量,应 用封闭系统在恒温、恒压、非体积功为零条件下的吉布斯函数 的增量作为判据来判断过程的自发性。 例5-1-5求1.00mol过冷水在101325Pa及-10℃时凝固过程的 △S。己知冰的质量熔化焓为334.7小g1,水和冰的质量热容分 别为CH0,1)=4.184Jg1-K-1,C,H20,s)=2.092Jg1K-1。 解: H20(1,263K)→H20(s,263K) 过冷水是在非两相平衡条件下凝固,因此是一个不可逆相变过 程。要计算其△S,可在同样始末态间设计可逆途径来进行
4 相变过程自发性判据 为了判断一个在指定条件下进行的相变过程能否自发进 行, 需要热力学判据。这样的判据有两个,一个是把系统和环境看 成是一个孤立系统,分别计算出系统和环境的熵变后,应用孤 立系统的熵变作为判据来判断过程的自发性。另一个是分别计 算出系统的焓变和熵变后,再计算系统的吉布斯函数增量,应 用封闭系统在恒温、恒压、非体积功为零条件下的吉布斯函数 的增量作为判据来判断过程的自发性。 例5-1-5 求1.00mol过冷水在101325Pa及-10℃时凝固过程的 △S。已知冰的质量熔化焓为334.7J·g-1,水和冰的质量热容分 别为Cp(H2O,1) = 4.184J·g-1·K-1,Cp(H2O,s) = 2.092J·g-1·K-1。 解: H2O(1,263K)→H2O(s,263K) 过冷水是在非两相平衡条件下凝固,因此是一个不可逆相变过 程。要计算其△S,可在同样始末态间设计可逆途径来进行

H,0(1) T2=263.15K T,P H,0(s)T2=263.15K 1mol p=101.325kPa △S 1mol p=101.325kPa P AS p△S3 H20(1) T1=273.15K T,P H0(s) T1=273.15K 1mol p=101.325kPa △S2 1mol p=101.325kPa As,-Jcg-c0n 273 =(1.00×18.0×4.184×ln JK1=2.81JK 263 =ao9=m9 3 T 263 =(1.00×18.0×2.092×ln )J.K=-1.41JK 273
H2O ( l ) T2 = 263.15K 1mol p=101.325kPa H2O ( s ) T2 = 263.15K 1mol p=101.325kPa H2O ( l ) T1 = 273.15K 1mol p=101.325kPa H2O ( s ) T1 = 273.15K 1mol p=101.325kPa T , p △S T , p △S2 p △S1 p △S3 ∫ ∆ = = 12 21 1 , , (l) (l)ln TT p m p m TT nC TdT S nC 1 1 )J K 2.81J K 263 273 (1.00 18.0 4.184 ln − − = × × × ⋅ = ⋅ 1 2 3 , , ( ) ( )ln 2 1 T T nC s T dT S nC s p m TT ∆ = p m = ∫ 1 1 )J K 1.41J K 273 263 (1.00 18.0 2.092 ln − − = × × × ⋅ = − ⋅