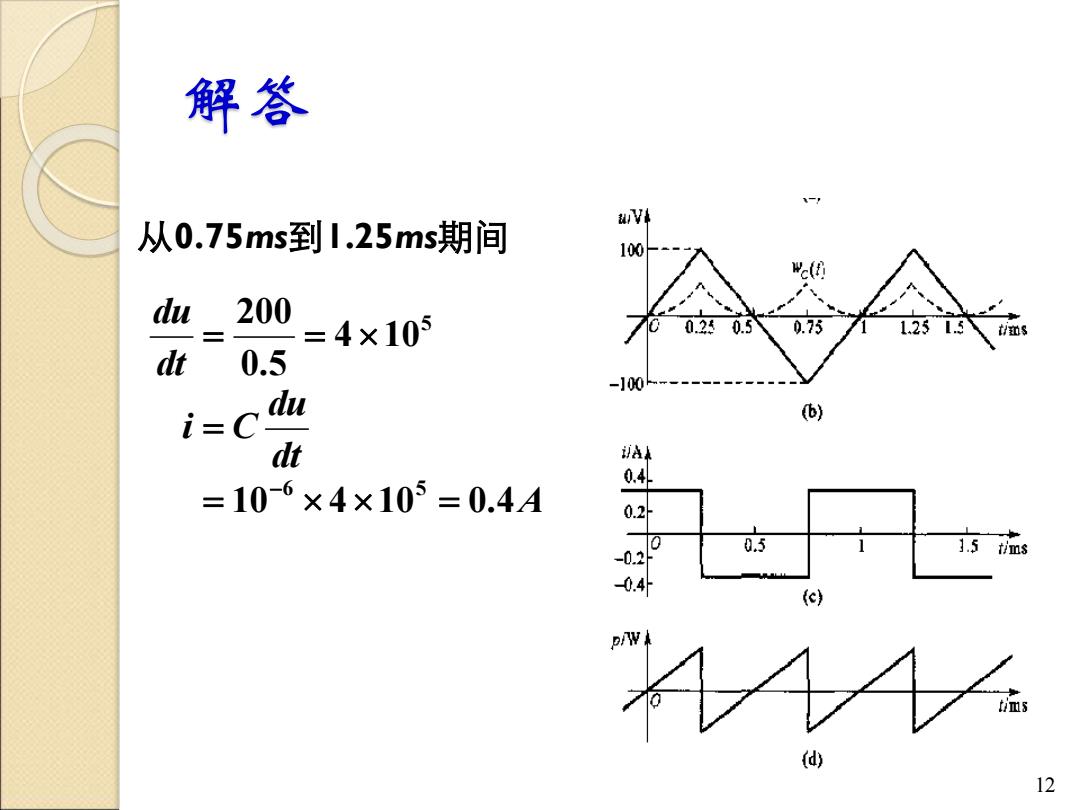
解答 -7 V 从0.75ms到1.25ms期间 100 "e( du 200 一 =4×105 0.250.5 0.75 1.25 l.3 道s dt 0.5 -00- du i=C (b) dt A 0,4 =10-6×4×105=0.4A 0.5 -02 1.5 tims 0.4 o/W tims 12
解答 从0.75ms到1.25ms期间 12 A dt du i C dt du 10 4 10 0.4 4 10 0.5 200 6 5 5 = = = = = −
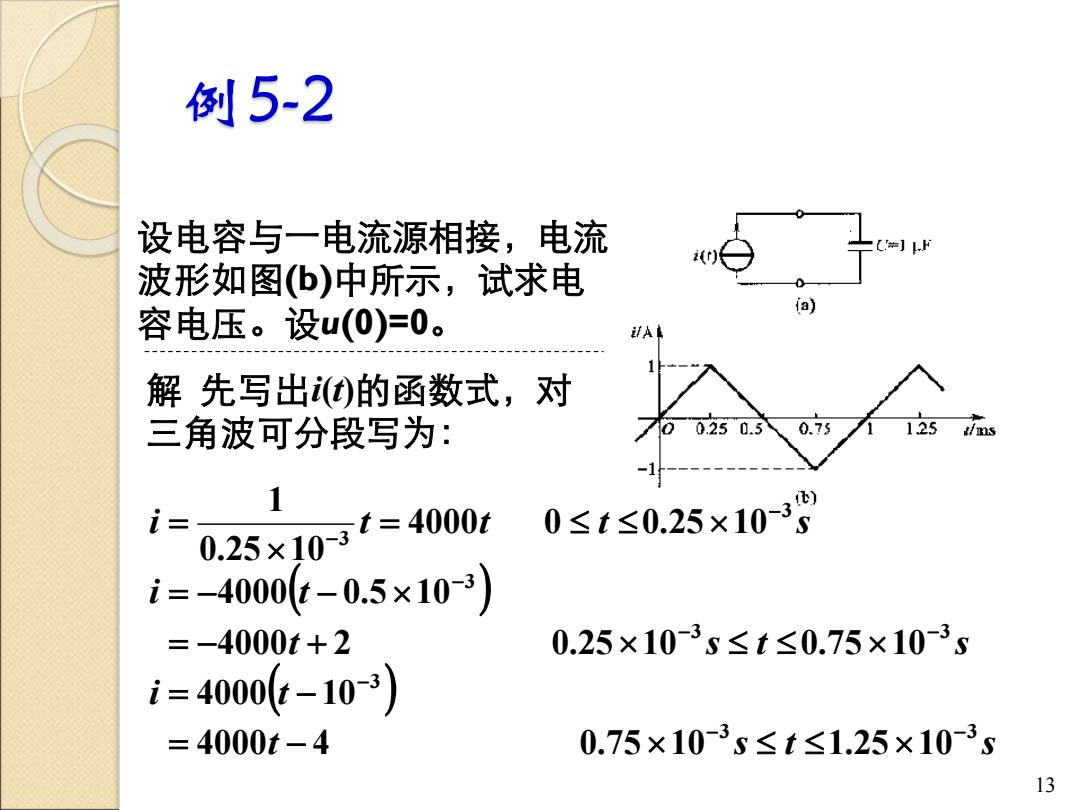
例5-2 设电容与一电流源相接,电流 ]LF 波形如图(b)中所示,试求电 容电压。设u(0)=0。 计Ai 解先写出)的函数式,对 三角波可分段写为: 760250.3 0.75 125 t/ms 1 i= 0.25x103t=4000r 0≤t≤0.25×103 i=-4000(t-0.5×10-3) =-4000t+2 0.25×10-3s≤t≤0.75×10-3s i=4000(-10-3) =4000t-4 0.75×10-3s≤t≤1.25×10-3s 13
例5-2 设电容与一电流源相接,电流 波形如图(b)中所示,试求电 容电压。设u(0)=0。 13 解 先写出i(t)的函数式,对 三角波可分段写为: ( ) ( ) t s t s i t t s t s i t i t t t s 3 3 3 3 3 3 3 3 4000 4 0.75 10 1.25 10 4000 10 4000 2 0.25 10 0.75 10 4000 0.5 10 4000 0 0.25 10 0.25 10 1 − − − − − − − − = − = − = − + = − − = =

解答 在0≤t≤0.25×10-3s期间 a)=a0)+i(传E=104000a5=-2×10't 当=0.25s时,u=125V。 在 0.25×103≤t≤0.75×10-3s期间 a)=0.25×10)+C2wi(55 =125+10i2x1o(40005+2)H5 =-250+2×106t-2×1092 此为一开口向下的抛物线,顶点在=0.5s、w=250V处。 当t=0.75s时,电压下降到125V。 14
解答 在 期间 14 当t=0.25ms时,u=125V。 此为一开口向下的抛物线,顶点在t=0.5ms、u=250V处。 当t=0.75ms时,电压下降到125V。 t s 3 0 0.25 10− ( ) ( ) ( ) 9 2 0 6 0 10 4000 2 10 1 0 i d d t C u t u t t = + = = t s 3 3 0.25 10 0.75 10 − − 在 期间 ( ) ( ) ( ) ( ) 6 9 2 0.2 5 1 0 6 0.2 5 1 0 3 250 2 10 2 10 125 10 4000 2 1 0.25 10 3 3 t t d i d C u t u t t = − + − = + − + = + = − −
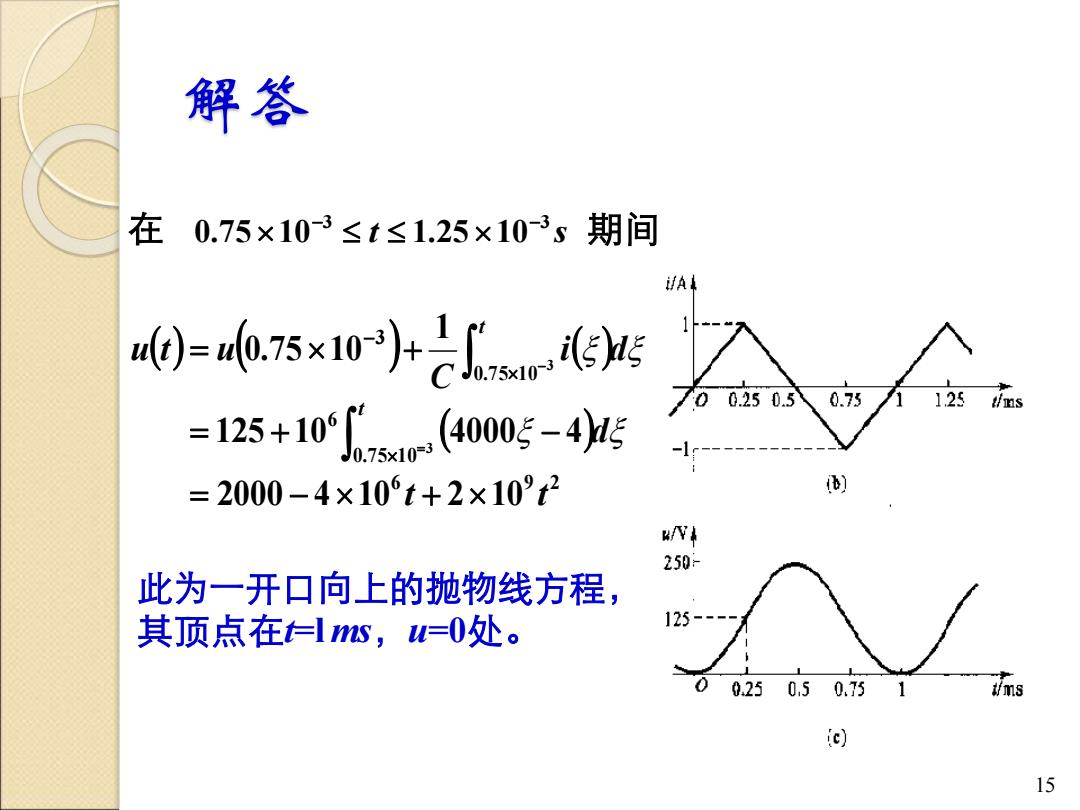
解答 在 0.75×10-3≤t≤1.25×10-3s期间 进A )=l75×10+乙arn〔5 00.250.5 0.75 1.25 t/ms =125+10i5ar(405-44 =2000-4×106t+2×1092 N 250- 此为一开口向上的抛物线方程, 其顶点在仁ls,=0处。 125--- 0 0.25 050.75 1 t/ms ic) 15
解答 15 此为一开口向上的抛物线方程, 其顶点在t=l ms,u=0处。 t s 3 3 0.75 10 1.25 10 − − 在 期间 ( ) ( ) ( ) ( ) 6 9 2 0.7 5 1 0 6 0.7 5 1 0 3 2000 4 10 2 10 125 10 4000 4 1 0.75 10 3 3 t t d i d C u t u t t = − + = + − = + = − −

§5-3电容电压的连续和记忆性质 电容电压的连续性质可陈述如下: ÷若电容电流i(t)在闭区间[t,tb]内为有界的,则电容电 压uc(t)在开区间(ttb)内为连续的。特别是,对任何 时刻t,且t.<t<tb uc(t)=uc(t) 即“电容电压不能跃变”,在动态电路分析问题中 常常用到这一结论。 16
§5-3 电容电压的连续和记忆性质 电容电压的连续性质可陈述如下: ❖ 若电容电流i(t)在闭区间[ta ,tb]内为有界的,则电容电 压uC(t)在开区间(ta ,tb )内为连续的。特别是,对任何 时刻t,且ta< t < tb 即“电容电压不能跃变”,在动态电路分析问题中 常常用到这一结论。 16 ( ) ( ) − = + u t u t C C