
动态电路的相量分析法和 $域分析法 第十章 频率响应 多频正弦稳态电路
第十章 频率响应 多频正弦稳态电路 动态电路的相量分析法和 s域分析法 1

§10-1基本概念 1.线性电路的网络函数 线性电路:由线性元件与独立电源组成的电路。 独立电源: 电路输入,激励(excitation) 线性 线性元件电流、电压: 电路的响应,由激励引起(resp系se) 网络函数: 对单一激励的线性、时不变电路,指定的响应对激励之比定 义为网络函数,记为H,即: H= 响应 激励 激励可以是电压源电压或电流源电流,响应可以是任一支路 的电压或电流。 2
§10-1 基本概念 2 1. 线性电路的网络函数 线性电路:由线性元件与独立电源组成的电路。 独立电源: 电路输入,激励(excitation) 线性元件电流、电压: 电路的响应,由激励引起(response) 网络函数: 对单一激励的线性、时不变电路,指定的响应对激励之比定 义为网络函数,记为H,即: 激励可以是电压源电压或电流源电流,响应可以是任一支路 的电压或电流。 线 性 关 系 激励 响应 H =

网络函数 ÷响应与激励在同一端口一策动点函数(driving point) ◆.占.卜一hk六.□ 山 古土工为乙1L.。。。C. 线性电阻电路网络函数H的分类 响应 激励 名称及专用符号 电流 策动点函数 电压 策动点电导G, 电压 电流 策动点电阻R, 电流 电压 转移电导G, 电压 电流 转移电阻R, 转移函数 电流 电流 转移电流比H 电压 电压 转移电压比H, 3
网络函数 ❖ 响应与激励在同一端口——策动点函数(driving point) ❖ 响应与激励不在同一端口——转移函数(transfer) 3
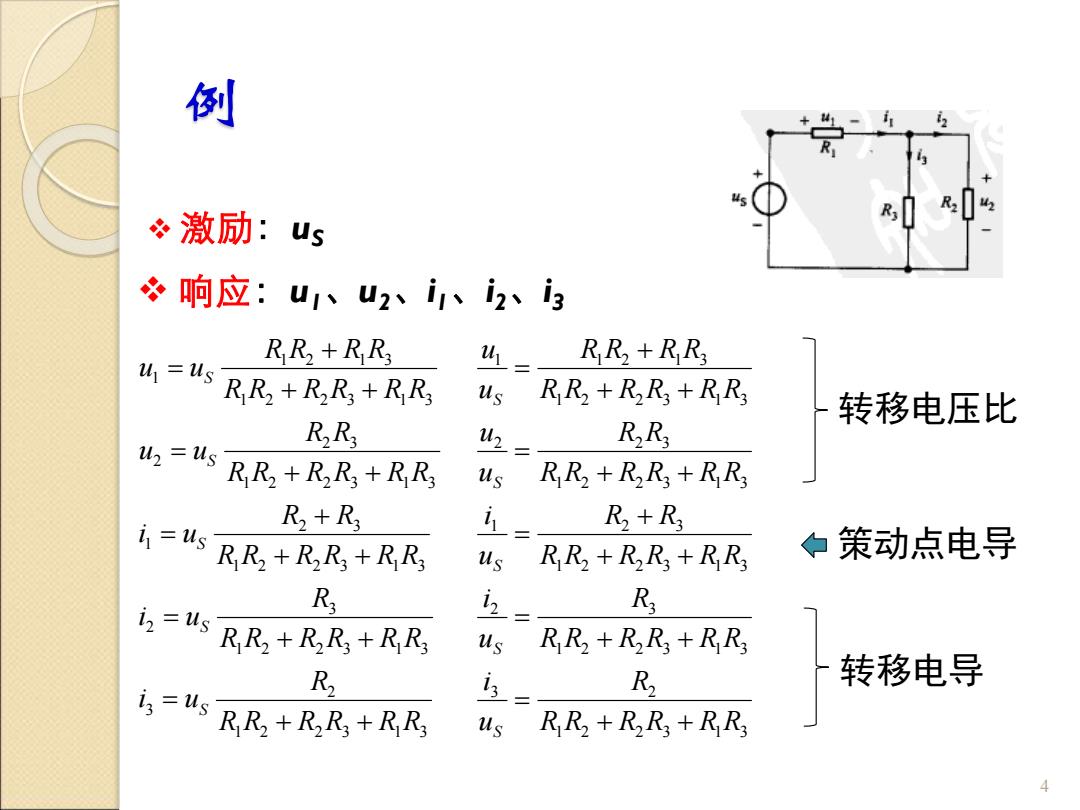
倒 冬激励:us 响应:u、u2、、2、3 RR+RR 4= RR+RR3 =us RR2+RzR;+RR3 us RR+RRs+RRs 转移电压比 RR 2二 RR ,=山RR+RR+RR us RR+RRs+RR3 R+R3 R+R3 i=us RR+RaR3+RR3 us RR+RR3+RR 策动点电导 R3 R3 i2=us RR+RaR+RR3 us RR+RRs+RRs R R 转移电导 i=4s RR+RaR;+Rks us RR+RR3+RR 4
例 ❖ 激励:uS 4 1 2 2 3 1 3 2 3 1 2 2 3 1 3 3 2 1 2 2 3 1 3 2 3 1 1 2 2 3 1 3 2 3 2 1 2 2 3 1 3 1 2 1 3 1 R R R R R R R i u R R R R R R R i u R R R R R R R R i u R R R R R R R R u u R R R R R R R R R R u u S S S S S + + = + + = + + + = + + = + + + = 转移电压比 1 2 2 3 1 3 3 2 1 2 2 3 1 3 2 3 1 2 2 3 1 3 1 2 3 1 2 2 3 1 3 2 2 3 1 2 2 3 1 3 1 1 2 1 3 R R R R R R R u i R R R R R R R u i R R R R R R R R u i R R R R R R R R u u R R R R R R R R R R u u S S S S S + + = + + = + + + = + + = + + + = ❖ 响应:u1、u2、i1、i2、i3 转移电导 策动点电导

线性电阻电路网络函数性质 实数:对任何线性电阻电路,网络函数都是实数 澈0 响应 H(实数) (电压戒电流) (电压或电流) 冬叠加性—一叠加原理 激励1[ 线性电阻 响应 电路 y))=∑Hnxn() 激励2☐ 当激励1≠0,激励2=0,响应=H1×激励1 激励1=0,激励2≠0,响应=H2×激励2 则激励1≠0,激励2≠0,响应=H1×激励1+H2×激励2 5
线性电阻电路网络函数性质 5 ❖ 实数:对任何线性电阻电路,网络函数都是实数 ❖ 叠加性——叠加原理 1 0, 2 0, H1 1 H2 2 1 0, 2 0, H2 2 1 0, 2 0, H1 1 则激励 激励 响应 激励 激励 激励 激励 响应 激励 当激励 激励 响应 激励 = + = = = = = M m m y(t) H x (t)