
冲激函数在动态电路分 杯中的应用 1
冲激函数在动态电路分 析中的应用 1
§-1冲激函数 单位冲激函数(unit impulse function)又称狄拉克涵 数,其定义为 [6t=0 ∀t≠0 6(t)at=1 单位冲激函数可以看成是脉冲函数p(t)在△→0时的极 限。当△减小时,脉冲函数的幅度/△增加,而PA()曲 线下的面积总保持为,当△趋近于零时,即为单位冲 激函数6t)。 (4) 1 面积=1 △ 2 2
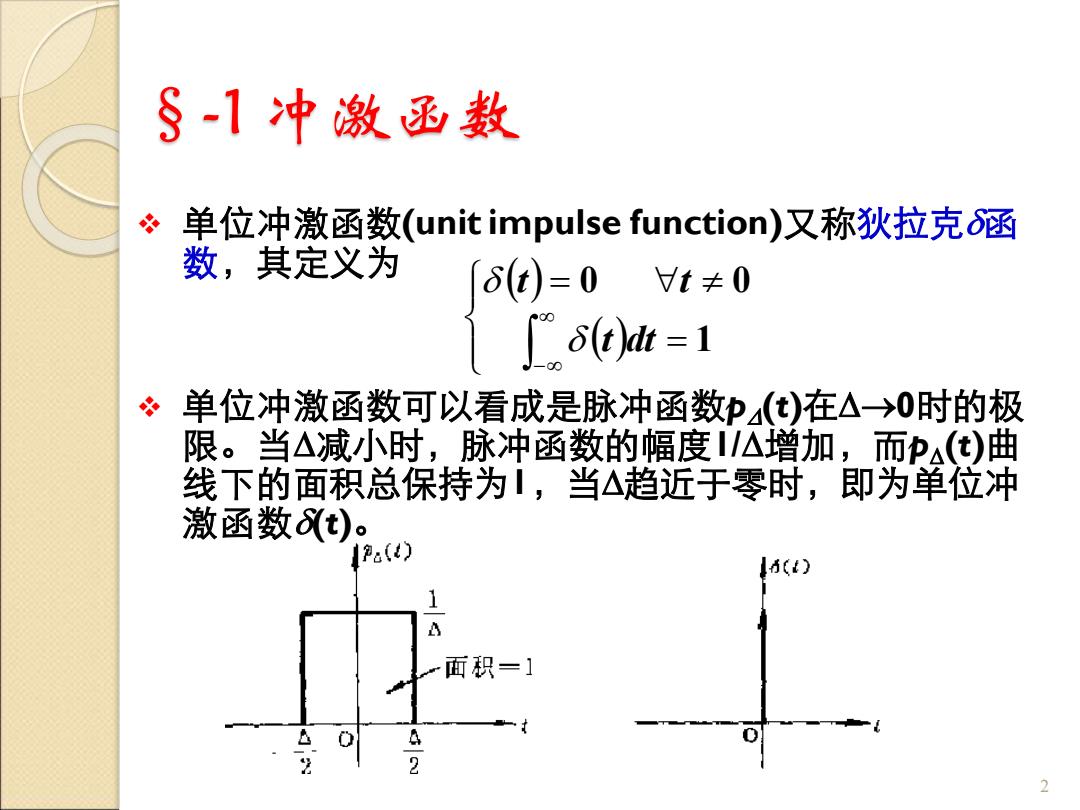
§-1 冲激函数 ❖ 单位冲激函数(unit impulse function)又称狄拉克函 数,其定义为 ❖ 单位冲激函数可以看成是脉冲函数p (t)在→0时的极 限。当减小时,脉冲函数的幅度1/增加,而p (t)曲 线下的面积总保持为1,当趋近于零时,即为单位冲 激函数(t)。 2 ( ) ( ) = = − 1 0 0 t dt t t

冲激函数的强度 冲激函数所含的面积称为冲激函数的强度,单位冲 激函数为强度为单位的冲激函数。 对冲激电流来说,其强度的量纲为安培秒,即库仑。 单位冲激电流是指强度为库仑,而不是指幅度为 单位(即1安培)的冲激电流。 冲激电流的幅度趋于无限大,移动的电荷为库仑, 这些电荷的移动是在极其短促(趋于零)的时间内完成 的,因而电流的幅度极大
冲激函数的强度 ❖ 冲激函数所含的面积称为冲激函数的强度,单位冲 激函数为强度为1单位的冲激函数。 ❖ 对冲激电流来说,其强度的量纲为安培·秒,即库仑。 单位冲激电流是指强度为1库仑,而不是指幅度为1 单位(即1安培)的冲激电流。 ❖ 冲激电流的幅度趋于无限大,移动的电荷为1库仑, 这些电荷的移动是在极其短促(趋于零)的时间内完成 的,因而电流的幅度极大。 3

单位延时冲激函数 ?单位延时冲激函数的定义为 [6lt-)=0t≠t 1δt-6)t=1 单位延时冲激函数t-t)可设想为:在=t处宽度趋于 零,而幅度趋于无限大,但具有单位面积的脉冲。 冬在t处强度为A的冲激函数记为A6tto)。对冲激电流 来说可表为26t-t);对冲激电压来6tt)。 4
单位延时冲激函数 ❖ 单位延时冲激函数的定义为 4 ( ) ( ) − = − = − 1 0 0 0 0 t t dt t t t t ❖单位延时冲激函数(t-t0 )可设想为:在t=t0处宽度趋于 零,而幅度趋于无限大,但具有单位面积的脉冲。 ❖在t0处强度为A的冲激函数记为A(t-t0 )。对冲激电流 来说可表为Q(t-t0 );对冲激电压来(t-t0 )

其他形状脉冲的极限情况 ?冲激函数一般看成是矩形脉冲函数的极限情况,其他 形状脉冲的极限情况也可作为单位冲激的近似。 具有单位面积的三角形脉冲,当△趋近于零时,可作 为单位冲激的近似。 f( 面积=1 十5 5
其他形状脉冲的极限情况 ❖ 冲激函数一般看成是矩形脉冲函数的极限情况,其他 形状脉冲的极限情况也可作为单位冲激的近似。 ❖ 具有单位面积的三角形脉冲,当趋近于零时,可作 为单位冲激的近似。 5