
以人 1.5克拉默法则(续1) 尚本 线性方程组(1.5.1) 的系数在保持原来的相 对位置不变的情况下构成n阶行列式 12 022 02n 0n2 a n 称为线性方程组(1.5.1) 的系数行列式 河套大学《线性代数》课件 第一章行列式 快东骨司
快乐学习 以人 为本 河套大学《线性代数》课件 第一章 行列式 1.5 克拉默法则(续1) , 1 2 21 22 2 11 12 1 n n nn n n a a a a a a a a a D = 线性方程组(1.5.1)的系数在保持原来的相 对位置不变的情况下构成 n 阶行列式 称为线性方程组(1.5.1)的系数行列式

水人 1.5克拉默法则(续2) 尚本 01,j-l b a.j 21 a2.j- b, a2.j+l 02n 031 a3,j- b3 03,j 。。。 03n ·g 0n-l月 An-1,j-1 An-1,j+l An-In an An,j-\ An,j+ ann 这里D,(有=1,2,,n)是把系数行列式D中的第列的 元素换成线性方程组(1.5.1) 的常数项b,b2,,bn所得 的n阶行列式. 河套大学《线性代数》课件 第一章行列式 快东学司
快乐学习 以人 为本 河套大学《线性代数》课件 第一章 行列式 1.5 克拉默法则(续2) n n j n n j n n n n j n n j n n j j n j j n j j n j a a b a a a a b a a a a b a a a a b a a a a b a a D 1 , 1 , 1 1,1 1, 1 1 1, 1 1, 3 1 3, 1 3 3, 1 3 2 1 2, 1 2 2, 1 2 1 1 1, 1 1 1, 1 1 − + − − − − − + − − + − + − + = 令 的 阶行列式. Dj ( j = 1,2, ,n) 是把系数行列式 D 中的第 j b b bn , , , 1 2 n 这里 元素换成线性方程组(1.5.1)的常数项 列的 所得

水人 1.5 克拉默法则(续3) 尚本 克拉默(Gramer)法则 定理1.5.1若线性方程组(⊥.1.5)的系数行列 式D≠0,则线性方程组(11.5)有唯一解 D X1 ,X2= 1.5.2) 三 解线性 分析证明方法:存在性,唯一性 方程组 河套大学《线性代数》课件 第一章行列式 快乐学司
, . D D x n , n = 1 1 D D x = 定理1.5.1 若线性方程组(1.1.5)的系数行列 式 ,则线性方程组(1.1.5) 快乐学习 以人 为本 河套大学《线性代数》课件 第一章 行列式 1.5 克拉默法则(续3) D 0 有唯一解 2 , . (1.5.2) 2 D D x = . 解线性 方程组 克拉默(Gramer)法则 分析证明方法:存在性,唯一性

水人 1.5克拉默法测 (续4) 尚本 证明首先,证明式((1.5.2)是方程组(1.5.1)的解 将x D(,2,一代入第k个方程的左端 +0k2 得aD D D D.(dD+) D D (1.5.3) 因为 D,=b41+b2421+…+b,A元 D2=b42+b2A2+…+bnAn2, 推理 所以 D.=bAn+b2A2n++4m 河套大学《线性代数》课件 第一章行列式 快东学司
个方程的左端, 快乐学习 以人 为本 河套大学《线性代数》课件 第一章 行列式 1.5 克拉默法则(续4) D D x j j = j = 1, 2 , ,n k ( ) 1 1 1 2 2 2 2 1 1 k k kn n n k k kn a D a D a D D D D a D D a D D a + ++ = + ++ 证明 首先,证明式(1.5.2)是方程组(1.5.1)的解. ( )代入第 (1.5.3) 将 因为 = + + + = + + + = + + + . , , 1 1 2 2 2 1 12 2 22 2 1 1 11 2 21 1 n n n n nn n n n n D b A b A b A D b A b A b A D b A b A b A 所以 得 推理
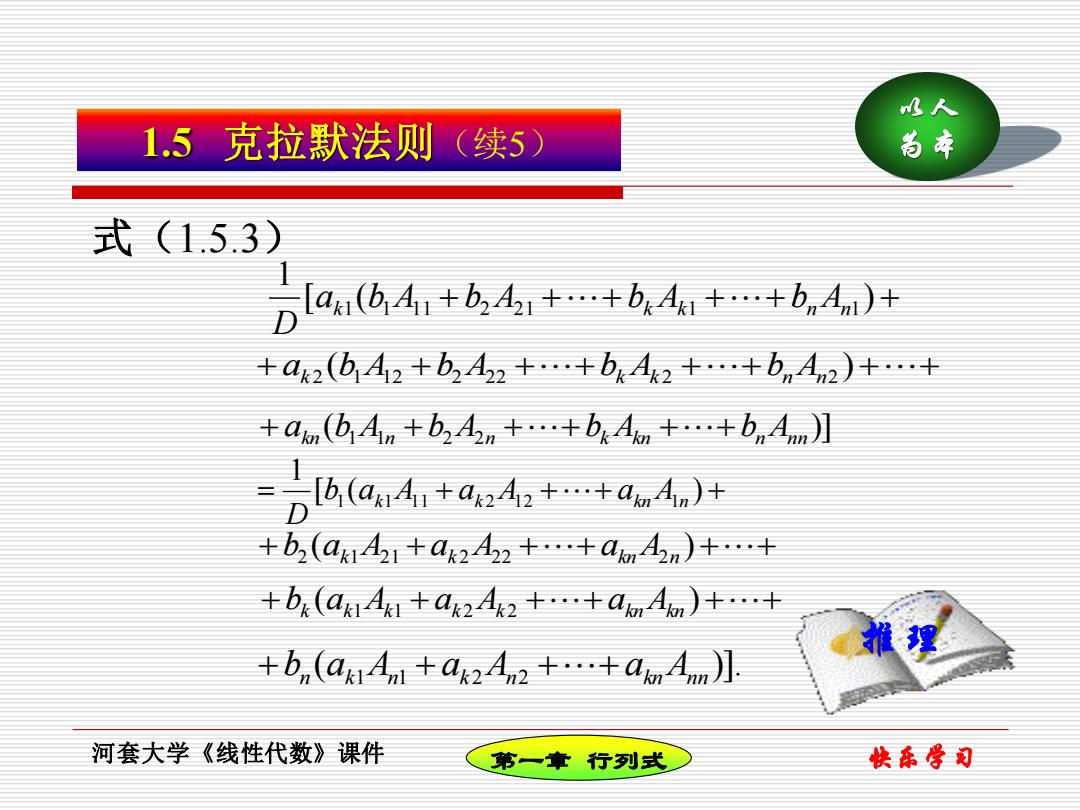
水人 1.5克拉默法则 (续5) 尚本 式(1.53) Dldu(+bdn) +a2(b42+b242+…+b42+…+bn4n2)+…± +a(b4n+b24n+…+bAm+…+bn Aun)】 =b,(a41+a24,+…+an4n) +b,(a41+a4242十…+an4n)+…t +b(aa4+a242+…+a4n)+ 推理 +b,(a14n1+a424n2+…+a,An月 河套大学《线性代数》课件 第一章行列式 快东学司
快乐学习 以人 为本 河套大学《线性代数》课件 第一章 行列式 [ ( + + + + + ) + 1 ak1 b1 A1 1 b2 A2 1 bk Ak1 bn An1 D + ak 2 (b1 A12 +b2 A22 ++bk Ak 2 ++bn An2 ) ++ ( )] + akn b1 A1n +b2 A2n ++bk Akn ++bn Ann = [ ( + + + ) + 1 b1 ak1 A1 1 ak 2 A1 2 aknA1n D +b2 (ak1 A21 + ak 2 A22 ++ aknA2n ) ++ +bk (ak1 Ak1 + ak 2 Ak 2 ++ aknAkn ) ++ ( )]. +bn ak1 An1 + ak 2 An2 ++ aknAnn 式(1.5.3) 1.5 克拉默法则(续5) 推理