
第四章 相似矩阵与与一次型 目录 4.1n 维向量的内积 四 4.2 ,矩阵的特征值与特征向量 14.3 相似矩阵 4.4二次型 4.5正定二次型 4.6应用举例 河套大学《线性代数》课件 第四章相似矩阵与二次型 快东学司
□ 4.1 维向量的内积 4.2 矩阵的特征值与特征向量 □ 4.3 相似矩阵 □ 4.4 二次型 □ 4.5 正定二次型 □ 4.6 应用举例 目录 快乐学习 n 河套大学《线性代数》课件 第四章 相似矩阵与二次型 第四章 相似矩阵与二次型
本节授裸计划 水人 (2课时) 尚本 必复习必新课 4.2矩阵的特征值与特征向量 4.2.1特征值和特征向量的概念 第三十次课 4.2.2特征值和特征向量的性质 4.2.3特征值和特征向量的求法 4.2.4特征值和特征向量的特征 父小结 必思考题及答案提示 必练习、作业及参考答案 河套大学《线性代数》课件 第四章相似矩阵与二次型 快乐学司
快乐学习 以人 为本 ❖复习 ❖新课 4.2 矩阵的特征值与特征向量 4.2.1 特征值和特征向量的概念 4.2.2 特征值和特征向量的性质 4.2.3 特征值和特征向量的求法 4.2.4 特征值和特征向量的特征 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 三 十 次 课 本节授课计划(2课时) 河套大学《线性代数》课件 第四章 相似矩阵与二次型
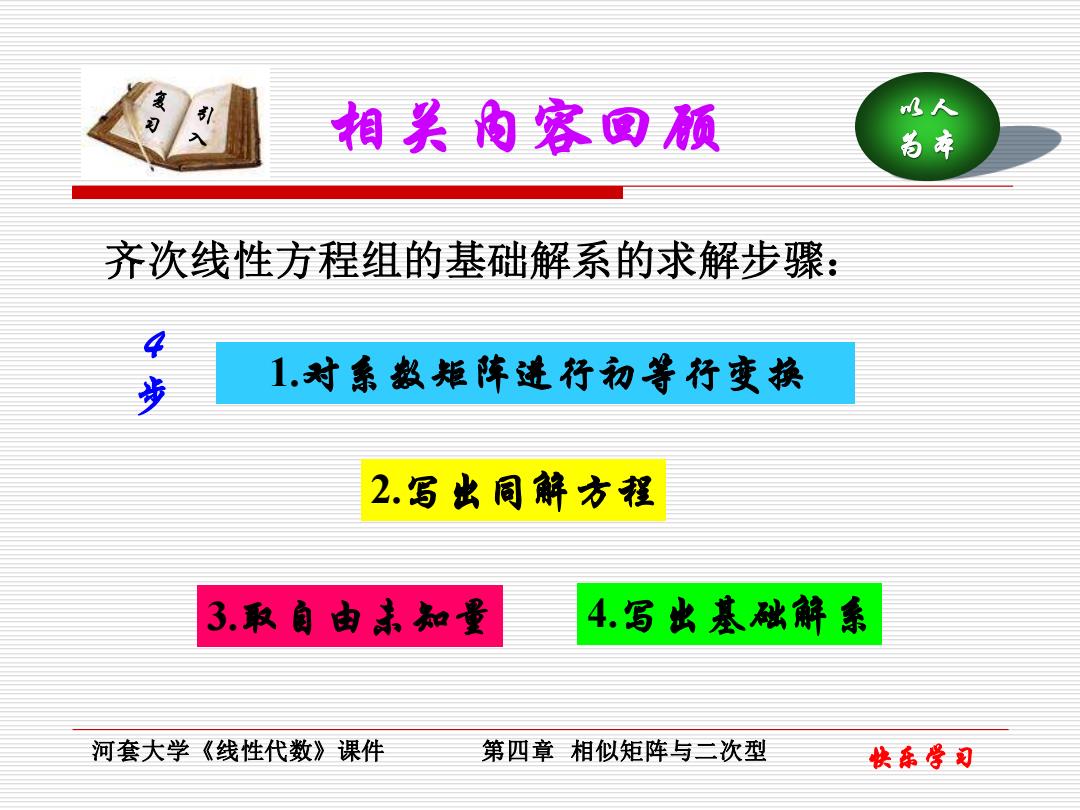
相关内容回预 水人 尚本 齐次线性方程组的基础解系的求解步骤: 4 1.对素数矩阵进行初等行变换 2.写出同解方程 3.取自由未知量 4.写出基础解素 河套大学《线性代数》课件 第四章相似矩阵与二次型 快东学司
快乐学习 以人 相关内容回顾 为本 河套大学《线性代数》课件 第四章 相似矩阵与二次型 齐次线性方程组的基础解系的求解步骤: 1.对系数矩阵进行初等行变换 2.写出同解方程 3.取自由未知量 4.写出基础解系 4 步

水人 4.2矩阵的特征值与特征向量 尚本 特征值 2.特征向量 3.特征方程 4,特征多项式 5.矩阵的迹 返回 河套大学《线性代数》课件 第四章相似矩阵与二次型 快东学司
快乐学习 以人 为本 主 题 词 4.2 矩阵的特征值与特征向量 返回 河套大学《线性代数》课件 第四章 相似矩阵与二次型 1.特征值 2.特征向量 3.特征方程 4.特征多项式 5.矩阵的迹

水人 新课 4.2.1特征值和特征向量的概念 1 尚本 定义4.2.1i 设A是n阶方阵,若存在实数人 和n维非零列向量5,使得 A5=九5, (4.2.1) 则称数入为矩阵A的特征值,称非零列向量5 为矩阵A的属于特征值入的特征向量: 河套大学《线性代数》课件 第四章相似矩阵与二次型 快乐学司
4.2.1 特征值和特征向量的概念 1 以人 新课 为本 河套大学《线性代数》课件 第四章 相似矩阵与二次型 快乐学习 定义4.2.1 设 A 是 n 阶方阵,若存在实数 n 维非零列向量 ,使得 A = (4.2.1) 和 , 则称数 为矩阵 A 的特征值,称非零列向量 为矩阵 A 的属于特征值 的特征向量