
第二章 矩阵 目录 四 2.1 矩阵的概念 四 2.2 矩阵的运算 2.3 逆矩阵(1) 四 2.4 矩阵的分块 四 2.5 初等变换与初等矩阵 四 2.6 矩阵的秩 四 2.7 应用举例 河套大学《线性代数》课件 第二章矩阵 快乐学司
第二章 矩 阵 2.1 矩阵的概念 2.2 矩阵的运算 ★ 2.3 逆矩阵(1) 2.4 矩阵的分块 2.5 初等变换与初等矩阵 2.6 矩阵的秩 2.7 应用举例 目录 河套大学《线性代数》课件 第二章 矩阵 快乐学习
本节授裸计划 水人 (2课时) 尚本 新课 2.3 逆矩阵 第十一次 2.3.1矩阵的转置 2.2.4矩阵可逆的充分必要条件 小结必思考题及答案提示 保 必练习、作业及参考答案 河套大学《线性代数》课件 第二章矩阵 快东学可
快乐学习 以人 为本 ❖新课 2.3 逆矩阵 2.3.1 矩阵的转置 2.2.4 矩阵可逆的充分必要条件 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 十 一 次 课 本节授课计划(2课时) 河套大学《线性代数》课件 第二章 矩阵

水人 2.3逆矩阵 尚本 主题调 1、可逆矩阵 2、 逆矩阵 3、 伴随矩阵法 4、 奇异矩阵 5、非奇异矩阵 返回 河套大学《线性代数》课件 第二章矩阵 快东学司
快乐学习 以人 为本 主 题 词 2.3 逆矩阵 河套大学《线性代数》课件 第二章 矩阵 1、可逆矩阵 2、逆矩阵 3、伴随矩阵法 4、奇异矩阵 5、非奇异矩阵 返回
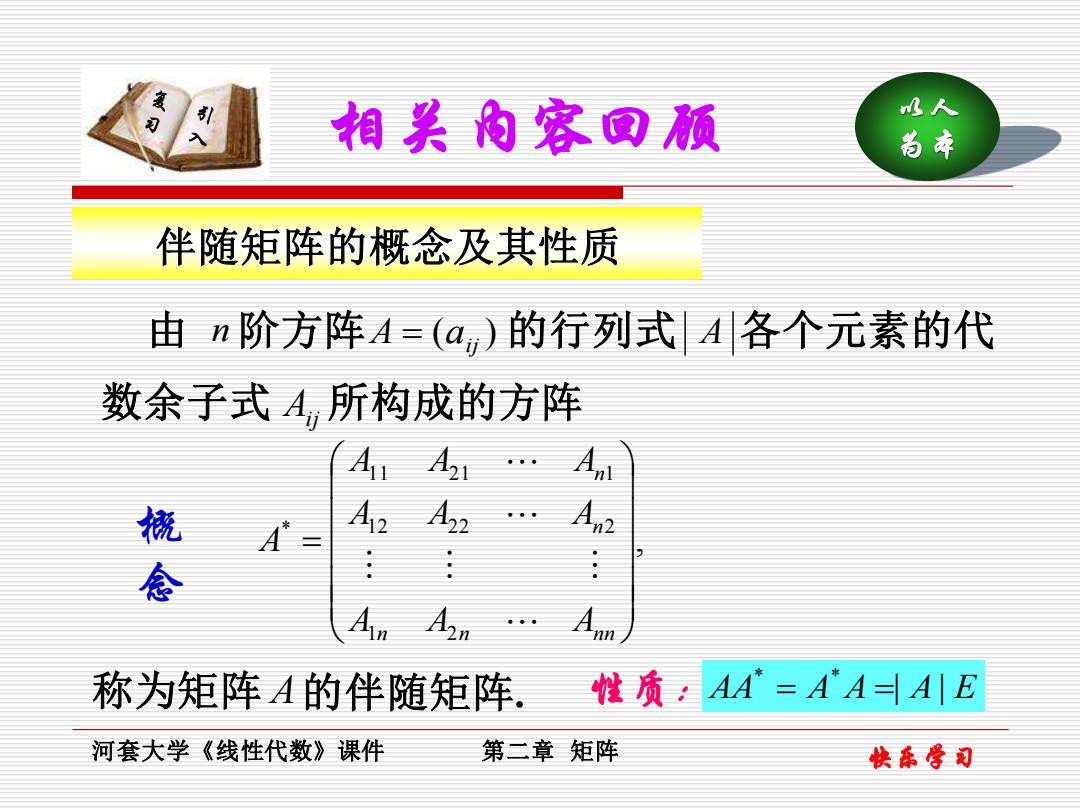
相关内容回预 水人 尚本 伴随矩阵的概念及其性质 由n阶方阵A=(a,)的行列式A各个元素的代 数余子式A,所构成的方阵 A A21 概 A2 A.n A 称为矩阵A的伴随矩阵. 性质?AA=AA三AE 河套大学《线性代数》课件 第二章矩阵 快东学司
数余子式 伴随矩阵的概念及其性质 快乐学习 以人 相关内容回顾 为本 河套大学《线性代数》课件 第二章 矩阵 n ( ) A = aij A Aij 由 阶方阵 的行列式 各个元素的代 所构成的方阵 , 1 2 12 22 2 11 21 1 * = n n n n n n A A A A A A A A A A 称为矩阵 A 的伴随矩阵. 性质: AA A A | A| E * * = = 概 念

水人 2.3.1逆矩阵的概念 尚本 精测:数有加法、减法、 乘法与除法运算,矩 阵也有加法、减法、乘法运算,那么,矩阵是否 也有除法运算呢 我们将2称为2的逆元,则221=1,一般地, 对于数a≠0,总存在唯一乘法逆元aI,使得 aa=1且aa=1.数的逆元在解方程中起着 重要作用例如,解一元线性方程ax=b,当a≠0 时,其解为x=ab=ba 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.3.1 逆矩阵的概念 为本 河套大学《线性代数》课件 第二章 矩阵 猜测:数有加法、减法、乘法与除法运算,矩 阵也有加法、减法、乘法运算,那么,矩阵是否 也有除法运算呢 1 ? 2 − 2 2 1, 1 = − a 0 −1 a 1 1 = − a a 1. 1 = − a a 我们将 称为2的逆元,则 且 一般地, 对于数 ,总存在唯一乘法逆元 ,使得 数的逆元在解方程中起着 重要作用.例如,解一元线性方程 ax = b ,当 a 0 . . −1 −1 时,其解为 x = a b = ba