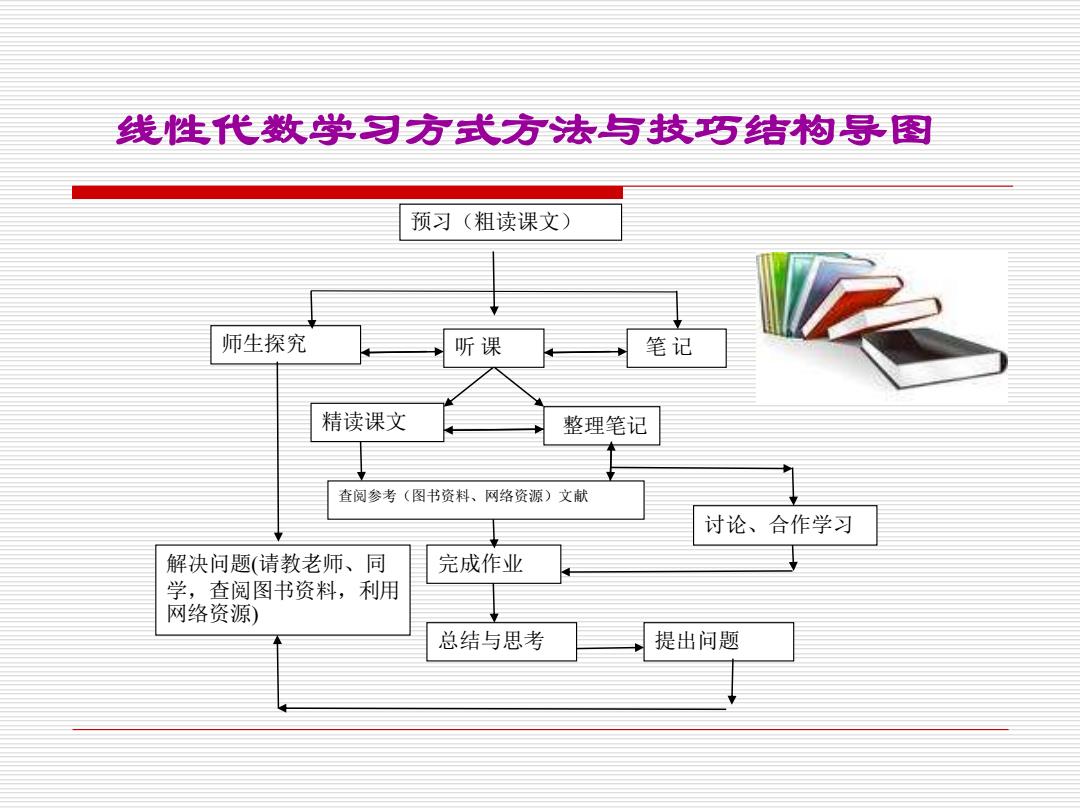
线性代数学习方式方法与技巧结构导图 预习(粗读课文) 师生探究 听课 笔记 精读课文 整理笔记 查阅参考(图书资料、网络资源)文献 讨论、合作学习 解决问题(请教老师、同 完成作业 学,查阅图书资料,利用 网络资源) 总结与思考 提出问题
师生探究 听 课 笔 记 查阅参考(图书资料、网络资源)文献 精读课文 整理笔记 完成作业 总结与思考 提出问题 讨论、合作学习 解决问题(请教老师、同 学,查阅图书资料,利用 网络资源) 预习(粗读课文) 线性代数学习方式方法与技巧结构导图

线性代数学习方式方法与技巧结构导图 理解 成绩评定: 作业:10%; 重要的 出勤:15%; 重要的 提问与测验:10%; 概念定义 笔记:5%; 背会 公式定理 熟记考试:60%. 掌握:推理、分类、类比、转化与化归、推广、从 特殊到一般、从一般到特殊等数学思想与方法
重要的 概念 定义 公式 定理 理解 重 要 的 背会 熟记 线性代数学习方式方法与技巧结构导图 成绩评定: 作业:10% ; 出勤:15% ; 提问与测验:10%; 笔记:5%; 考试:60%. 掌握:推理、分类、类比、转化与化归、推广、从 特殊到一般、从一般到特殊等数学思想与方法

第一章 行列式 目录 ★1.1二阶和三阶行列式 四1.2n阶行列式 四1.3行列式的性质 四1.4行列式的计算 四1.5克拉默法则 河套大学《线性代数》课件 快乐学司
第一章 行列式 ★ 1.1 二阶和三阶行列式 1.2 阶行列式 1.3 行列式的性质 1.4 行列式的计算 1.5 克拉默法则 n 目录 河套大学《线性代数》课件 快乐学习

第一章 行列式 人人 尚本 行列式实质上是由一些数排列成的数表按 定法则计算得到的一个数,即是一种特定的算式. 在1683年与1693年,日本数学家关孝和 (Seki 历史与发展 K0wa,1642-1708)与德国数学家莱布尼茨 (Leibniz,1646-1716)就分别独立地提出了行列 式的概念在以后很长一段时间内,行列式主要应 用于对线性方程组的研究.大约一个半世纪以后, 行列式逐步发展成为线性代数的一个独立分支. 河套大学《线性代数》课件 第一章行列式 快东骨司
第一章 行 列 式 在1683年与1693年,日本数学家关孝和(Seki Kowa,1642-1708)与德国数学家莱布尼茨 (Leibniz,1646-1716)就分别独立地提出了行列 式的概念.在以后很长一段时间内,行列式主要应 用于对线性方程组的研究. 大约一个半世纪以后, 行列式逐步发展成为线性代数的一个独立分支. 快乐学习 行列式实质上是由一些数排列成的数表按一 定法则计算得到的一个数, 历 史 与 发 展 以人 为本 河套大学《线性代数》课件 即是一种特定的算式. 第一章 行列式

水人 行列式的而史与发展 尚本 1750年,瑞士数学家克拉默 (Cramer, 1704-1752)在他的论文中提出了利用行列式求解 线性方程组的著名法则一一克拉默法则.随后 法国数学家柯西(Cauchy,1789-1857)发现了 行列式在解析几何中的应用.这一发现激起了人 们对行列式应用进行探索的浓厚兴趣,前后持续 了近100年.在柯西所处的时代,人们讨论的行列 式的阶数通常很小,行列式在解析几何以及数学 的其它分支中都扮演着很重要的角色 河套大学《线性代数》课件 第一章行列式 快东学日
河套大学《线性代数》课件 快乐学习 1750年,瑞士数学家克拉默 (Cramer , 1704-1752)在他的论文中提出了利用行列式求解 线性方程组的著名法则——克拉默法则. 随后, 法国数学家柯西(Cauchy,1789-1857)发现了 行列式在解析几何中的应用. 这一发现激起了人 们对行列式应用进行探索的浓厚兴趣,前后持续 了近100年. 在柯西所处的时代,人们讨论的行列 式的阶数通常很小,行列式在解析几何以及数学 的其它分支中都扮演着很重要的角色. 行列式的历史与发展 以人 为本 第一章 行列式