
图 14. 3.1从 z≤α 和 :=β 处起始的波沿着 α,β 为常数的线传播,并在 P点会合对初始条件的响应对初始时刻1=0时的V和I的分布的说明可导出两个行波。画出图14.3.1所示的在21平面上场的演变是有用的。在这-平面,上,,α=常数和 β=常数两特征线是直线,并分别具有斜率士c当=0时,沿轴给出(14)V(2,0) =V;(2)(15)I(z, 0) =1(2)在共后某一时刻1,这些场,例如在图14.3.1中的P点,该是怎么样呢?我们分两步回答此问题。首先,我们用初始条件去建立当10时刻,在每一位置上的两个分量V和V-。为此目的,把式(14)和(15)所示的初始条件代入方程(9)和(10)的左端,可得到包含这些未知数的两个方程。(16)++V-=-V(17)(V4-V.)=1解这两个方程就能待到用初始条件表示的两个分量。(18)V+=-(I,Z。+V)(19)=号(-1,Ze+V)第二步,把这些分量合成以得到图 14.3.1中P点的场。这里,我们利用沿α等于常数的线上的不变最V.和沿β等于常数的线上的不变量V-,把这些分量在 P点合成以给出 V和I 的方法已通过式(9)和(10)概括。在P点的总电压是这两个分量之和,而电流则是特征导纳Z:乘以该二分最之差下面的例子说明初始条件如何确定不变盈(在士方向传播的波V)和这些不变量如何依次确定在后续时间和不同位置,上的场。它们表明了图14.3.1中在P点的响应是如何由图中z491 :

二α和2=β两个位置上的初始条件确定的。隐含在我们对动态现象的理解中的是因果关系。某一时刻以后 P 点的响应是由以速度c向+方间传播的在(之=α,t=0)处的条件和以速度c向一方向传播的在(z=β,t=0)处的条件的结果。例14.3.1一个纯行波的激发在例3.1. 1中,我们介绍了包含单一分量向十2方向行进的均勾平面被。这是因为选择E,和H,的特殊的初始案件L (3. 1. 9)和(3. 1. 10)使响应只包含沿 +≥方向的行波。 若给定 E,的初始分布是(20)E,(z,0) B,(2) -Eee-r/2我们能否选择一个H,的分布,使它设有沿—z方向传援的响应部分!把传输线应用于平而波,并与(14.1.9)作如下的替换ue(21)VEr,leZ,H通过使(19)式的右端为零,我们可确信E_=0,于是使(22)H,-/E,=/Re**从式(18)和(19)可得,沿经过(z,0)的特征线(23)根据式(9)和(10)可得相继的场分布(24)(25)H,-/e E,=VeEe这蓝就是在例3.1.1中用“因难的方法求得的现磁行波下面的例子用来进一步说明图14.3.1中P点的场从(z=a,t=0)和(z=β,t=0)导得的两个过程。首先,V+和V两分鼠分别在(z=α,t=0)和(zβ,=0)处根据初始条件导得。因为V.沿α=常数和V.沿β=常数的线是不变的,我们可将这些分量合成去确定P点的场。例14.3. 2波瞬变的开始假设当=0时,在—和z=之间有均勾电呢",但在此范困以外V=0。假设在起始时刻,在沿线的全长上7=0。V,"s(26)2<-d和2>a√和「以后的分布如彻呢几我们求得了这些响应,我们将看到这些初始条件是如何在物班上实现的。初始条件图示在图14.3.2中,那里分别用实线和能线分有示出觉t-0时刻的V(z0)=V,I(20)=1由式(18)和(19)可得0:a<-d,d<<--d,d<p(27)Iypi-d<a<d,-d<B<d现在已经用初始条件识别了波的分量,就可用式(9)和(10)去建立相继的V和I的分布。它们也在图14.3. 2,在这个图上示出的是初始的以及相继的两个场中用垂直于z-t平面的轴表示V(z,t)(实线)或I(z,t)(虚线)。的分布。在点P,V,和V。均为零,所以V和I两者也都是零。在象P,这样的点上,从z=d传来的波已经到达,但是从z三一α来的被尚未到达,因此V,是V,/2,而V。仍为零。在象P,这样的点上,不论从z沿一2方向传播的被或者从。沿+z方向传播的波都尚末到达,V,和V.都由式(27)给出,因此场仍保持其初好状态。: 492 :
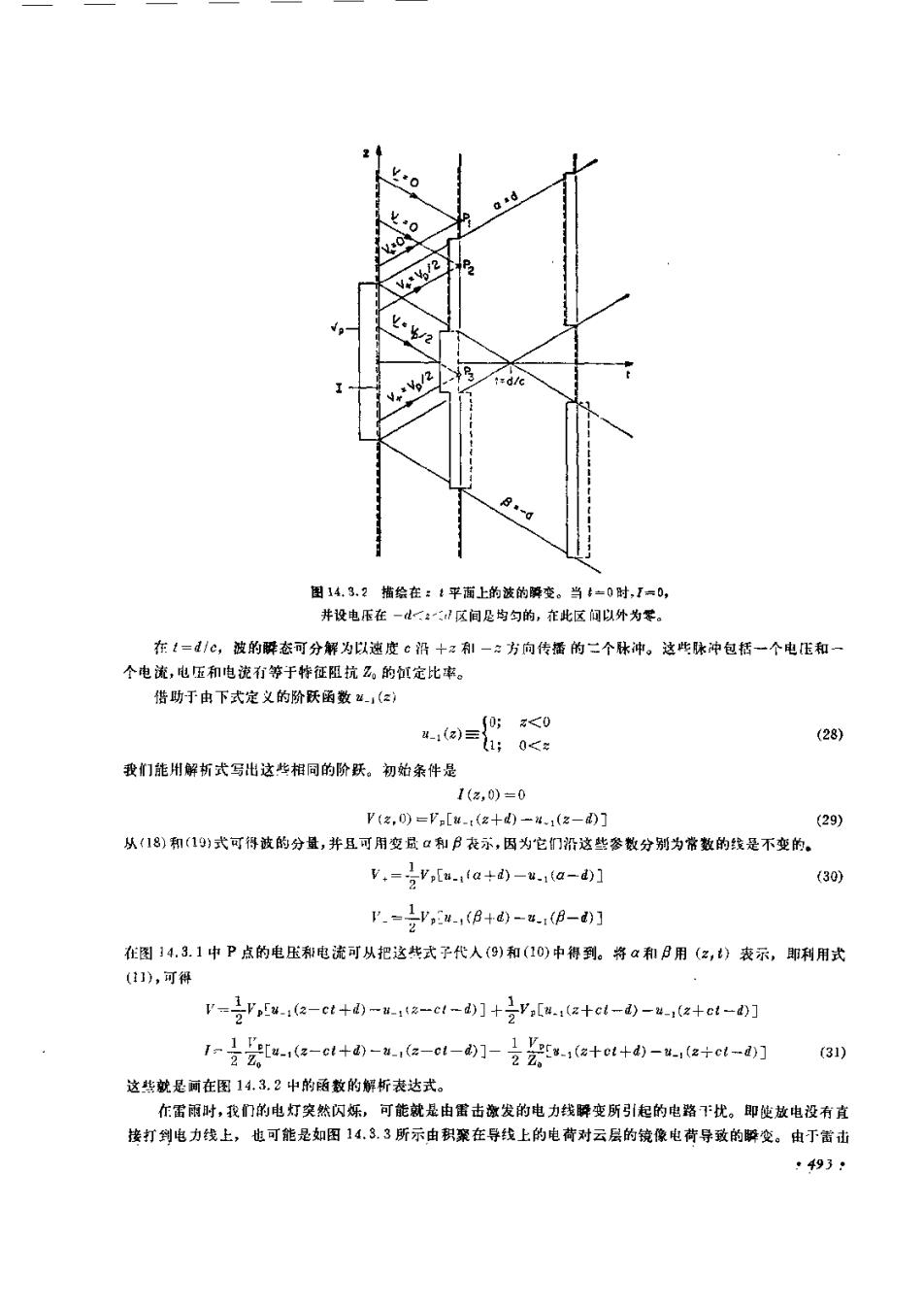
图 14. 8. 2 描绘在:1平面上的波的瞬变。当 1=0时,1=D,并设电压在一#21区间是均勾的,在此区间以外为零t=dlc,波的瞬态可分解为以速度c沿十TA一方向传播的二个脉冲。这些脉冲包括一个电压和个电流,电压和电流有等于特征阻抗Z。的征定比率。借助于由下式定义的阶跃函数 2-1(z)0; <0(28)(我们能用解析式写出达些相同的阶跃。初始条件是1(z,0)V(z,0) -V,[u-r(z+d) u-1(z-ad))(29)从(18)和(19)式可得波的分量,并且可用变员α和β衰示,因为它们沿这些参数分别为常数的线是不变的。+=vpu-ffa+d)-a-(30)P.--Vpu-,(β+d)-2-(β-d)I在图14.3.1中P点的电压和电流可从把这式子代人(9)和(10)中得到。将α和β用(z,t)表示,即利用式(11),可律(2ct-d)l+=Vp[u-r(z+ct-dz+c--1eru-(-ct+-ui(aci-d)]-- /Ew-1(+et+d)-u-,(z+cl-d))(31)这些就是画在图14.3.2中的函数的解析表达式。在雷丽时,我们的电灯突然闪烁,可能就是由雷击激发的电力线瞬变所引起的电璐下扰。即使效电没有直,也可能是如图14.3.3 所示由积案在导线上的电荷对云层的镜像电荷导致的瞬变。由于雷击接打到电力线上: 493 :
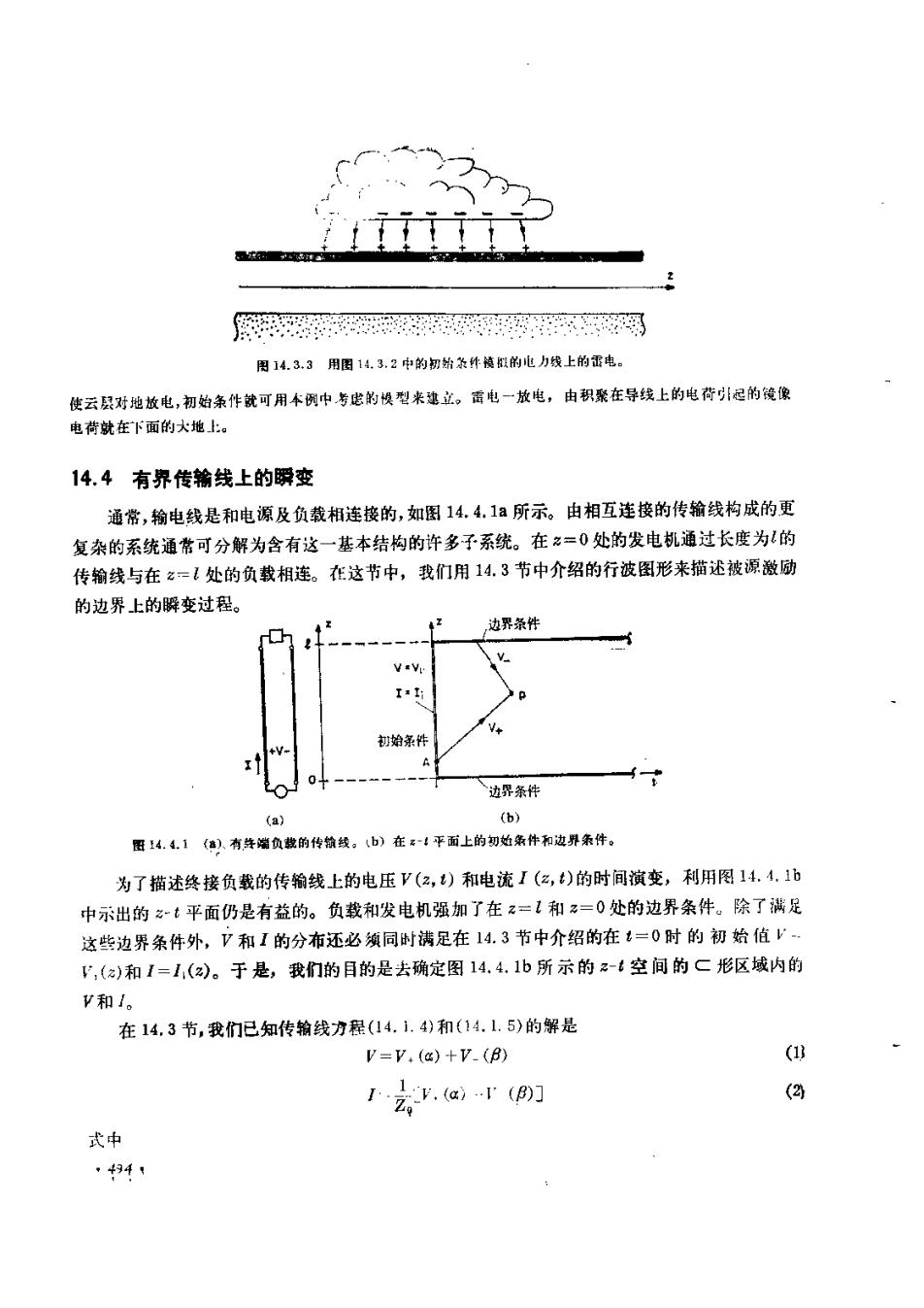
在导线上的电荷引起的镜像使云层对地放电,初始条作就可用本例中中考虑的模型来建立电荷就在下面的大地上14.4 有界传输线上的瞬变通常,输电线是和电源及负载相连接的,如图14.4.1a所示。由相互连接的传输线构成的更复杂的系统通常可分解为含有这一基本结构的许多子系统。在≥=0处的发电机通过长度为1的传输线与在2=1处的负载相连。在这节中,我们用14.3节中介绍的行波图形来描述被源激励的边界上的瞬变过程。边界条件边界条件h费的传输线。平面上的切始条件和边界条#14.4鲜为了描述终接负载的传输线上的电压V(z,t)和电流I(z,t)的时间演变,利用图14.4.1b中示出的-t平面仍是有益的。负载和发电机强加了在z=和 z=0处的边界条件。除了满足这些边界条件外,√和I的分布还必须同时满足在14.3节中介绍的在t=0时的初始值VV,(a)和 I=1(2)。于是,我们的目的是去确定图 14.4. 1b 所示的 -t 空间的 C 形区域内的V和1在14,3节,我们已知传输线力程(14.1.4)和(14.1.5)的解是(1)V=V. (α)+V.(β)(2).(a)(B))式中434 1

B=z+et(3)--ct:并且有c=1/VLC及Z=VL/0。说明V.和V.分别表示十和—z方向的行波的数学方式是说在z—1平面上沿α=常数和β=常数的特征线,这些最是不变显。确定V和I有两个步骤。·第,初始条件以及现在的边界条件,都是用于确定在2-平而,上沿二族特征线上的V和V-的。这是动态过程在时间增大的“方向”演变的意义上在因果关系占优的条件下所做的。于是,在特征线进人图14.4.1b中的C形区域向右边之处设置着对该线的不变量。·第二,在α常数和β常数两直线的给定的交点上:的解可按照式(1)和(2)确定。这第二可描述在图11.4.1b中。用物理术语来说,总电压或总电流是沿着在所关心的点相交的特征线传播的行波的叠加。为完成第一步,注意经过一给定点P的特征线可能有三个来源,第一,它可起始十「=0的轴上,在此情况下,不变量V决定于初始条件。对14.3节所讨论的无限长传输线,这是仪有的可能性。图14.4.2中,在特征线起始处当1=0,可用初始电压和电流计算式(1)和(2),这两个表达式的联立解即为所求的不变量。V42(Vi+ Zot)(4)V-=→(Vi-Zol)(5)图14.4.8起源于负投的特延线。图14.4.2起源于初始条件的特证线特征线的第二个发源点是在≥=1的边界,如图14.4.3所示、特殊地,我们考虑负载电阻RL为施加下列边界条件的终端V(1, t)=RtI(, 0)(6)许多问题将说明,我们这里的方法将如何同样适用于包括任意的电路终端情况。当然,纯电阻负载是最重要的终端情况,其理由很快就会清楚。又因为现象是随+“方向"行进,人射波 V+和在α=1处的边界条件共同确定了从=处的边界发源的在β=常数的特征线上的反射波V-(见图14.4. 3)。用数学语言表示,我们把(1)和(2)代人(6)495: