华东理工大学：《线性代数》课程电子教案（PPT课件）第五章 特征值问题与二次型

工王王王王二二王二二二王王 二、特征值与特征向量的求法 1求4-(， 的特征值和特征向量 解A的特征多项式为 A-2I= 3-2 -1 =(3-2)2-1 -1 3-元 =8-62+22=(4-2)(2-2) 解特征方程A-I=0 即得4的特征值为入1=2，入2=4

二、特征值与特征向量的求法 例1 . 1 3 3 1 求 的特征值和特征向量      − − A = A的特征多项式为   − − − − 1 3 3 1 (3 ) 1 2 = − − 8 6 (4 )(2 ) 2 = −  +  = −  −  2, 4. 1 2 即得A的特征值为 =  = A− I = 解特征方程 A− I = 0 解

当入，-2时，对应的特征向量应满足 a08 即 Jx1-X2=0, 一X1+X2=0. 解得x=,所以对应的特征向量取为p,=得c0 当入2=4时，由 3-01-0

      =               − − − − = 0 0 1 3 2 3 2 1 2 , 2 1 1 x x 当 时 对应的特征向量应满足    + = − = − 0. 0, 1 2 1 2 x x 即 x x , 解得x1 = x2 , 0. 1 1 1          所以对应的特征向量可取 为 p = c c , 0 0 1 1 1 1 , 0 0 1 3 4 3 4 1 4 , 2 1 2 1 2       =               − − − −       =               − − − − = x x x x 即 当 时 由

解得X,=一X2,所以对应的特征向量可取为 p.-dajcce -110 例2求矩阵A=-430 的特征值和特征向量 1 02 解A的特征多项式为 -1-2 1 0 A-AI= -4 3-2 0 =(2-)1-2), 1 0 2-λ 区回

, 0. 11 p,2 1 2    − = = − c c 解 得 x x 所以对应的特征向量可取 为 例２ . 1 0 2 4 3 0 1 1 0 求矩阵 的特征值和特征向量   −− A = 解 (2 ) , 1 0 2 4 3 0 1 1 0 (1 )2       = − − − − − − − A− I = A的特征多项式为

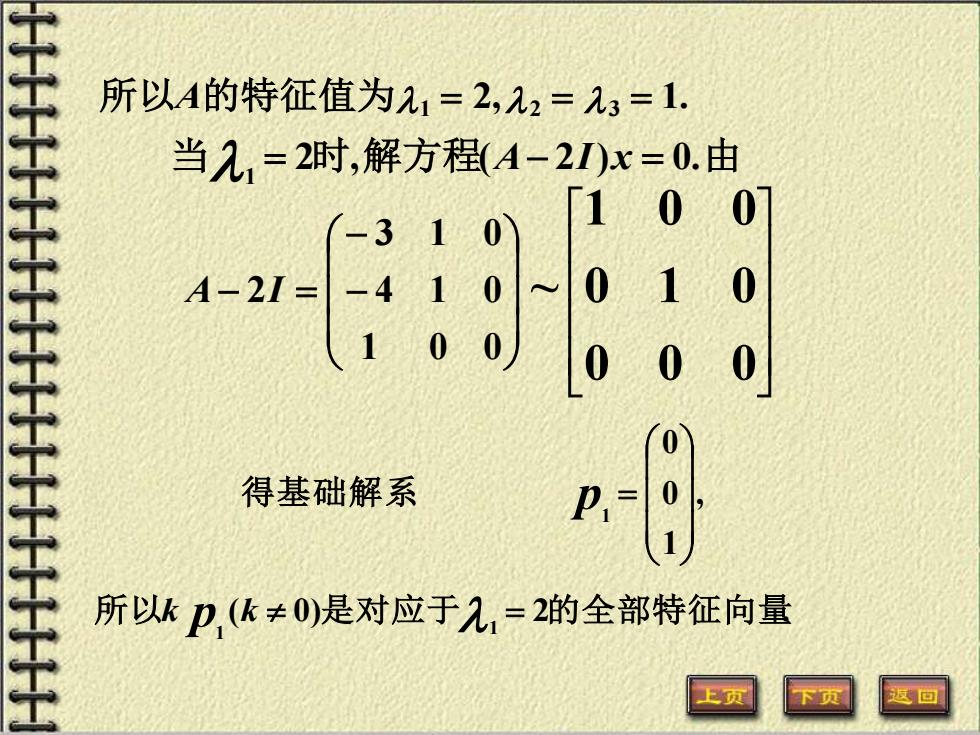
所以A的特征值为21=2,22=23=1. 当几1=2时，解方程(A-2I)x=0.由 -310 10 0 A-2I= -4 1 0 01 0 100 0 0 0 得基础解系 所以k卫，(k≠0)是对应于2，=2的全部特征向量 区回

2, 1. 所以A的特征值为1 = 2 = 3 = 当1 = 2时,解方程(A− 2I)x = 0.由                       − − − = 0 0 0 0 1 0 1 0 0 ~ 1 0 0 4 1 0 3 1 0 A 2I , 1 0 0 1           得基础解系 p = ( 0) 2 . 1 1 所 以k p k  是对应于 = 的全部特征向量

当入2=入3=1时，解方程(A-I)x=0由 10 A-1- 得基础解系 P2= 所以kp,(k≠0)是对应于几2=几，=的全部特征 向量

, 0 0 0 0 1 2 1 0 1 1 0 1 4 2 0 2 1 0 ~                     − − A− I = 当2 = 3 = 1时,解方程(A− I)x = 0.由 , 1 2 1 2           − − 得基础解系 p = 所以 ( 0)是对应于 2 3 1的全部特征 2 k p k   =  = 向量