
P:=m(-veI sin p-vc2 COs -vC3) =m-osn45-5 ocos0-21@) 2 12 5 2 2 2 3-N2)=-22ml0 √ 1 P,m(veI cosop+vc2 sin e) AB m(lcos4 losin 0) 2 1 B =mlo 2 2 2 x 777n7 √2mlo 2
2 2 ) 10 1 2 5 2 2 2 1 ( m l m l = = + ( cos sin ) Py = m vC1 + vC2 ( sin cos ) x C1 C2 C3 P = m −v −v −v cos 2 ) 2 5 sin 45 2 1 = m(− l − l − l ml 2) 2 2ml 10 3 2 5 2 2 2 1 = (− − − = − sin ) 2 5 cos 45 2 1 = m( l + l
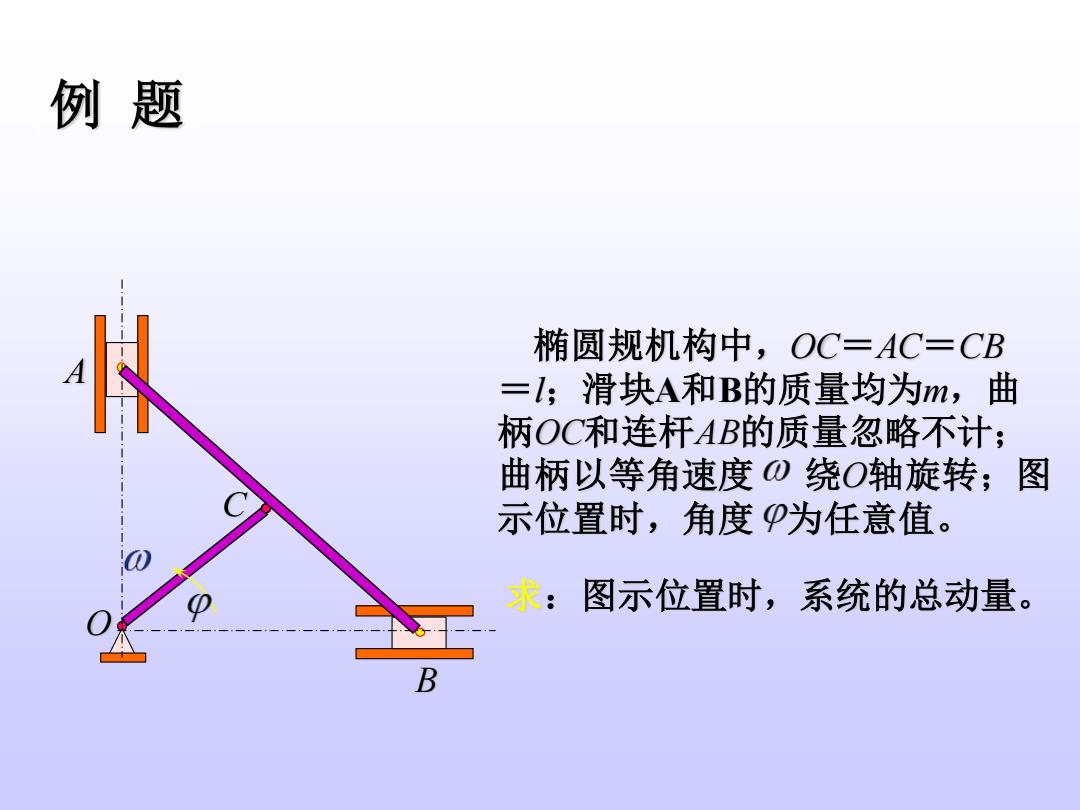
例题 椭圆规机构中,OC=AC=CB =1;滑块A和B的质量均为m,曲 柄OC和连杆AB的质量忽略不计; 曲柄以等角速度0绕O轴旋转;图 示位置时,角度P为任意值。 求:图示位置时,系统的总动量。 B
例 题 A O B 求:图示位置时,系统的总动量。 椭圆规机构中,OC=AC=CB =l;滑块A和B的质量均为m,曲 柄OC和连杆AB的质量忽略不计; 曲柄以等角速度 绕O轴旋转;图 示位置时,角度 为任意值
[方法一】 解:先计算各个质点的动量,再求 其矢量和。 P=mava+mBvB 建立O)y坐标系。在角度P为任意 VA 值的情形下 y=2lsin p,x=2lcoso VA=少4=2l0c0S0 VB =xg =2l@sin p P=2lmo(sin pi+cosi) VB X B
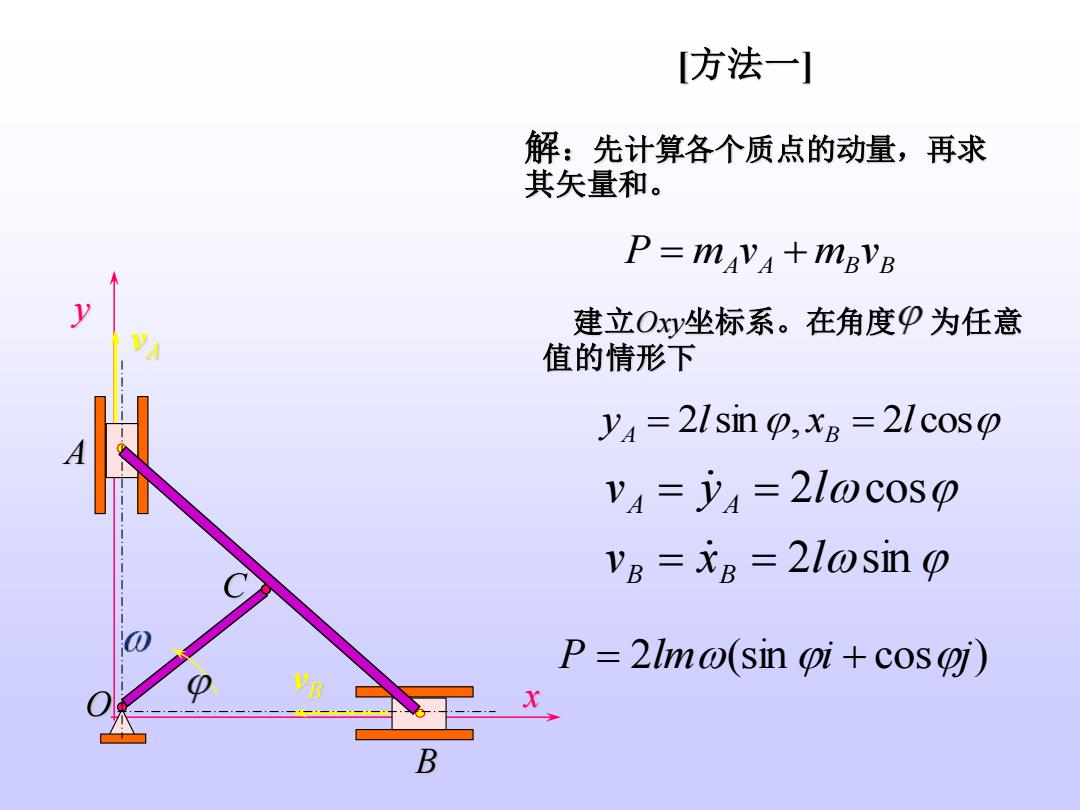
[方法一] 解:先计算各个质点的动量,再求 其矢量和。 x y vB vA 建立Oxy坐标系。在角度 为任意 值的情形下 A O B yA = 2lsin, xB = 2l cos A A B B P = m v + m v 2 sin 2 cos v x l v y l B B A A = = = = P = 2lm(sin i + cosj)
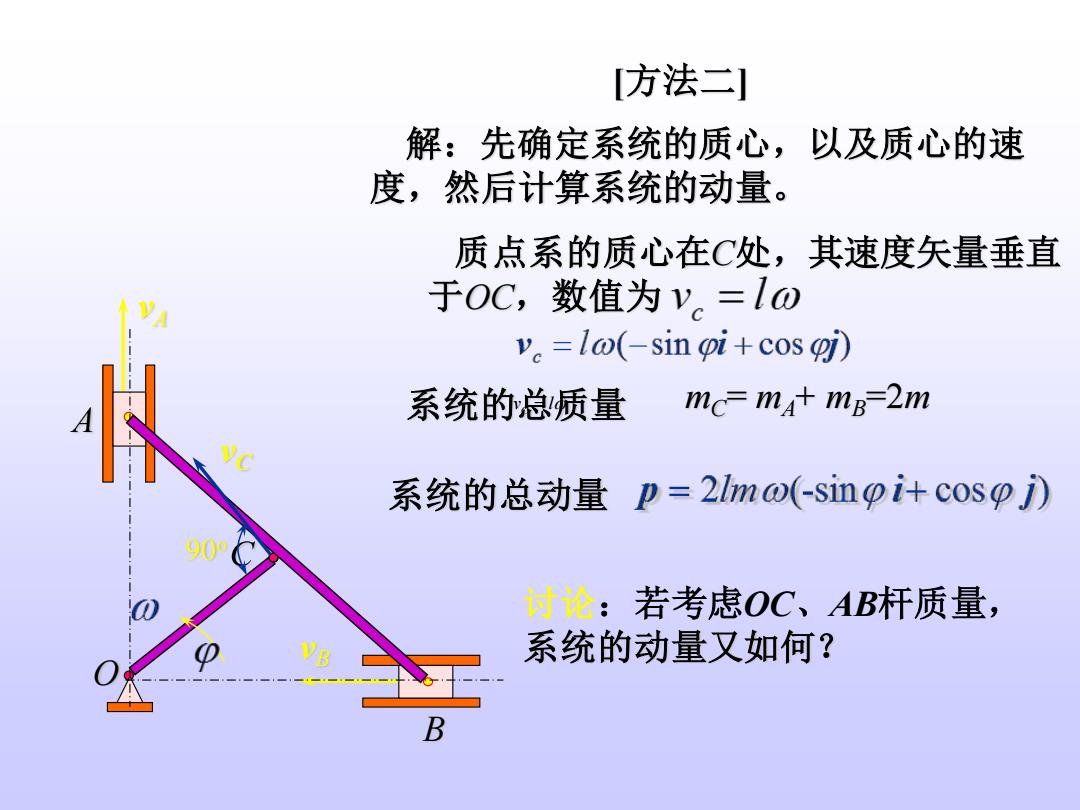
方法二] 解:先确定系统的质心,以及质心的速 度,然后计算系统的动量。 质点系的质心在C处,其速度矢量垂直 于OC,数值为y。=Io v.=la(-sin pi+cos i) 系统的总质量 mc=mat mB-2m 系统的总动量p=2lmo(-sinoi-+cosp) 909 讨论:若考虑OC、AB杆质量, VB 系统的动量又如何? B
vB vA A O B 解:先确定系统的质心,以及质心的速 度,然后计算系统的动量。 系统的总质量 mC= mA+ mB=2m 系统的总动量 vC 90o [方法二] 讨论:若考虑OC、AB杆质量, 系统的动量又如何? 质点系的质心在C处,其速度矢量垂直 于OC,数值为 vC = l