saga1常用校正方法:反馈校正 ©特点 一般无附加放大器,所要元件比串联校正少 ·信号从高功率点传向低功率点 ·校正后的性能主要决定于校正装置 ·与被反馈校正装置所包围的系统固有部分特性无关 ©优点:可抑制系统的参数波动及非线性因素对系统性能的影响 ©缺点:设计相对较为复杂 R(s) C(s) G(s) G2(s) G(S) H(s)
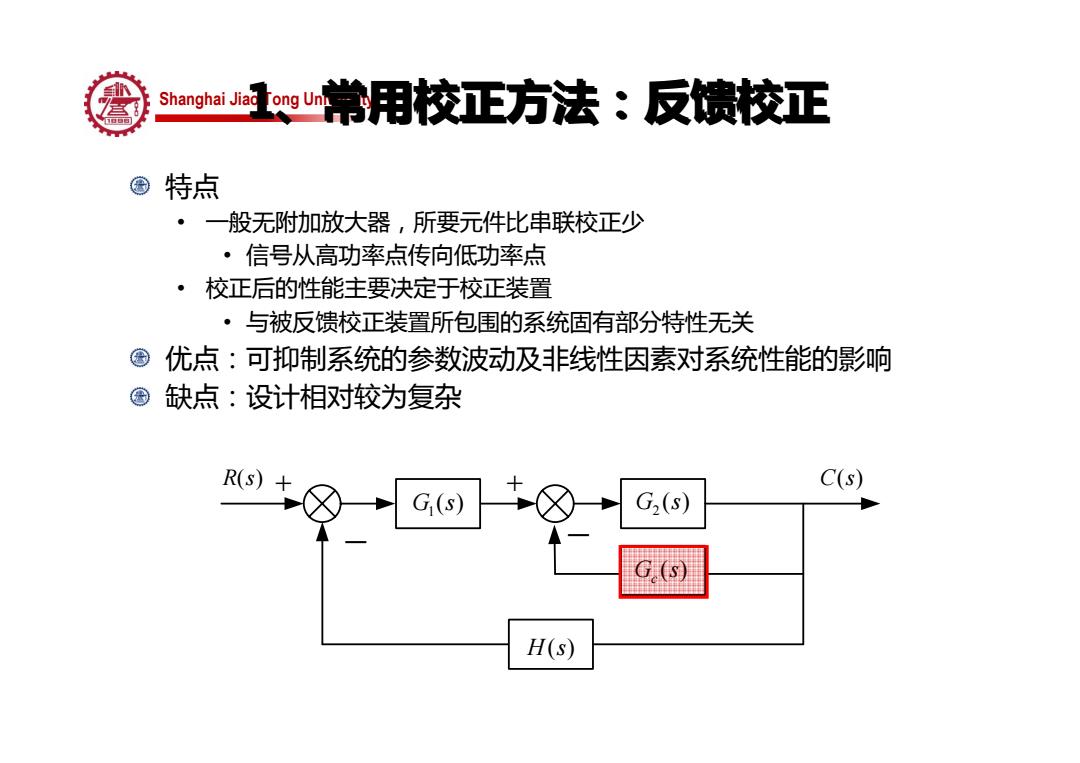
Shanghai Jiao Tong University 1、常用校正方法:反馈校正 1、常用校正方法:反馈校正 特点 • 一般无附加放大器,所要元件比串联校正少 • 信号从高功率点传向低功率点 • 校正后的性能主要决定于校正装置 • 与被反馈校正装置所包围的系统固有部分特性无关 优点:可抑制系统的参数波动及非线性因素对系统性能的影响 缺点:设计相对较为复杂 1 G s( ) 2 G s( ) ( ) G s c H( )s R s( ) + + C s( ) − −
sga1常用校正方法:前馈校正 ©输入控制方式,干扰控制方式 ©不影响系统的闭环特征方程式 ·其输入取自闭环外 ©基于开环补偿的办法来提高系统的精度 ·一般不单独使用,和其他校正方式结合应用而构成复合控制 系统 N(s) i(s R(s) C(s) E(s) C(s) G(s) G,(s) G(s) G(s) H(s) H(s) 前馈校正(输入) 前馈校正(干扰)
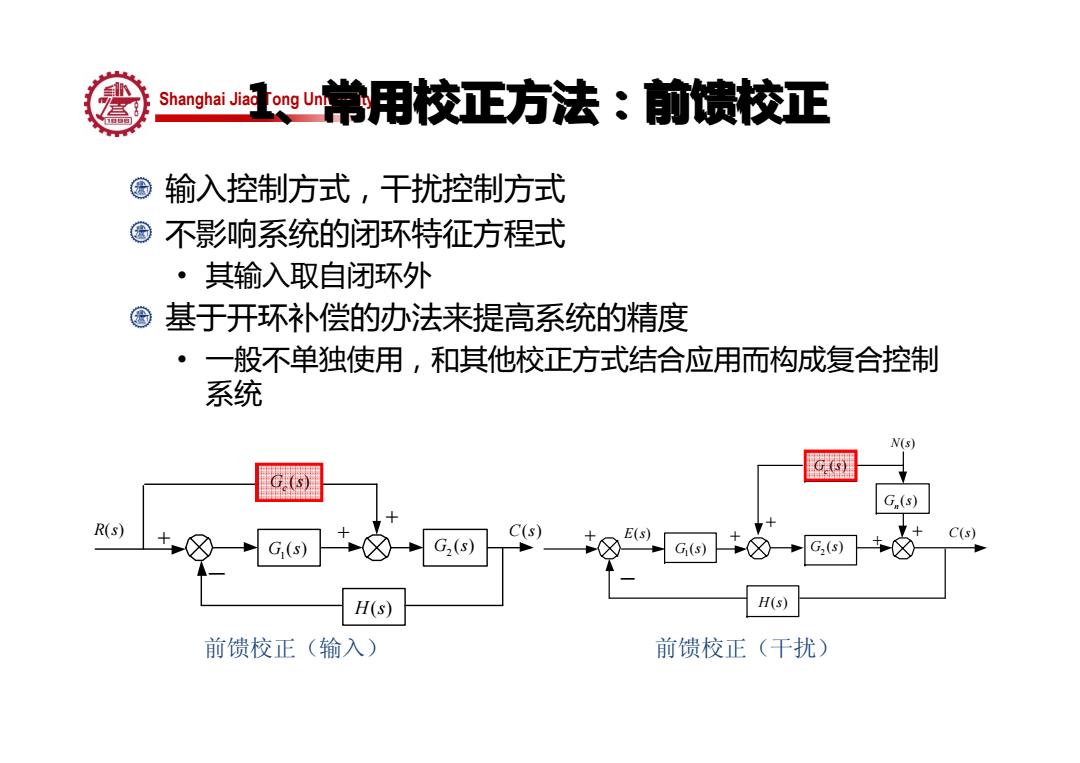
Shanghai Jiao Tong University 1、常用校正方法:前馈校正 1、常用校正方法:前馈校正 输入控制方式,干扰控制方式 不影响系统的闭环特征方程式 • 其输入取自闭环外 基于开环补偿的办法来提高系统的精度 • 一般不单独使用,和其他校正方式结合应用而构成复合控制 系统 + C s( ) + + + N s( ) E( )s 2 G s( ) 1 G s( ) ( ) G s c ( ) G s n H( )s + − 1 G s( ) ( ) G s c H( )s + C s( ) + + − 2 G s( ) R( )s 前馈校正(输入) 前馈校正(干扰)

sang1o常用校正方法:无源和有源 按有无放大能力来分: 无源校正装置 有源校正装置 通常由RC网络组成 通常由运算放大器和RC网络 共同组成 自身无放大能力 自身具有能量放大与补偿能 力 信号传递中,会产生幅值衰减 易于进行阻抗匹配 输入阻抗低,输出阻抗高 常需要引入附加的放大器,补偿幅值衰减和 进行阻抗匹配 通常被安置在前向通道中能量较低的部位上 使用范围广泛
Shanghai Jiao Tong University 1、常用校正方法:无源和有源 1、常用校正方法:无源和有源 按有无放大能力来分: 无源校正装置 有源校正装置 通常由RC网络组成 通常由运算放大器和RC网络 共同组成 自身无放大能力 自身具有能量放大与补偿能 力 信号传递中,会产生幅值衰减 输入阻抗低,输出阻抗高 常需要引入附加的放大器,补偿幅值衰减和 进行阻抗匹配 易于进行阻抗匹配 通常被安置在前向通道中能量较低的部位上 使用范围广泛

ShanghaiJ Tong Universi、系统性能指标 ©系统性能 稳定性:系统工作的前提 稳态特性:反映了系统稳定后的精度 。 动态特性:反映了系统响应的快速性 目标:稳定性强,稳态精度高,动态响应快 ©E 时域指标 超调量op、过渡过程时间t,、峰值时间t。、上升时 间t 国 频域指标 开环:增益剪切频率0。、 相位裕量、增益裕量Kg 闭环:谐振峰值M,、谐振频率or、带宽ob
Shanghai Jiao Tong University1、系统性能指标 1、系统性能指标 系统性能 • 稳定性:系统工作的前提 • 稳态特性:反映了系统稳定后的精度 • 动态特性:反映了系统响应的快速性 • 目标:稳定性强,稳态精度高,动态响应快 时域指标 • 超调量 σ p、过渡过程时间t s、峰值时间t p、上升时 间t r 频域指标 • 开环:增益剪切频率 ω c、相位裕量 γ、增益裕量K g • 闭环:谐振峰值M r、谐振频率 ω r、带宽 ω b

Shanghai Jiao Tong University 1、系统性能指标 时域 复域 频域 数学模型 微分方程 传递函数 频率特性 分析方法 分析法 根轨迹法 频率法 运动方程特征根 闭环传递函数的极点 相位裕量y>0 稳定性 具有负实部 分布在$的左半平面 增益裕量K。>1 稳态 由运动方程的系 对应的开环根轨迹增益K1 取决于低频段特性,型号数 性能 数决定 越大,es越小 相同,低频段幅值越大, ess越小 过渡过程时间t。 取决于系统主导极点位 取决于中频段的特性,相位 动态 越短,最大超调 置,主导极点距虚轴越 裕量γY越小,振荡越厉害, 性能 量o。越小,动 近,系统振荡越厉害 ●阻尼比系数ξ 增益剪切频率0。越大,响应 态特性越好 ●无阻尼自然频率on 速度越快
Shanghai Jiao Tong University 1、系统性能指标 1、系统性能指标 时域 复域 频域 数学模型 微分方程 传递函数 频率特性 分析方法 分析法 根轨迹法 频率法 稳定性 运动方程特征根 具有负实部 闭环传递函数的极点 分布在s的左半平面 相位裕量γ >0 增益裕量Kg >1 稳态 性能 由运动方程的系 数决定 对应的开环根轨迹增益K1 越大,ess越小 取决于低频段特性,型号数 相同,低频段幅值越大, ess越小 动态 性能 过渡过程时间ts 越短,最大超调 量σp 越小,动 态特性越好 取决于系统主导极点位 置,主导极点距虚轴越 近,系统振荡越厉害 阻尼比系数ξ 无阻尼自然频率ωn 取决于中频段的特性,相位 裕量 γ 越小,振荡越厉害, 增益剪切频率ωc越大,响应 速度越快