
Chapter 5 H2 PID Controllers for Stable Plants 4口,+@,4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 1/78
Chapter 5 H2 PID Controllers for Stable Plants Zhang, W.D., CRC Press, 2011 Version 1.0 1/78

H2 PID Controllers for Stable Plants 15.1 H2 PID Controllers for the First-Order Plant 25.2 Quantitative Tuning of H2 PID Controllers 35.3 H2 PID Controllers for the Second-Order Plant 45.4 Control of Inverse Response Processes 55.5 PID Controllers Based on the Maclaurin Series Expansion 65.6 PID Controllers with the Best Achievable Performance 75.7 Choice of the Filter 4口,+@,4定4定0C Zhang.W.D..CRC Press.2011 Version 1.0 2/78
H2 PID Controllers for Stable Plants 1 5.1 H2 PID Controllers for the First-Order Plant 2 5.2 Quantitative Tuning of H2 PID Controllers 3 5.3 H2 PID Controllers for the Second-Order Plant 4 5.4 Control of Inverse Response Processes 5 5.5 PID Controllers Based on the Maclaurin Series Expansion 6 5.6 PID Controllers with the Best Achievable Performance 7 5.7 Choice of the Filter Zhang, W.D., CRC Press, 2011 Version 1.0 2/78

Section 5.1 H2 PID Controllers for the First-Order Plant 5.1 H2 PID Controllers for the First-Order Plant An analog of Hoo optimal control theory:H2 optimal control theory Assume that the plant is Ke-0s G(s)= Ts+1 Using the Youla parameterization,we have C(s)= Q(s) 1-G(s)Q(s) where Q(s)is a stable transfer function.It is difficult to treat e-s analytically.Approximate it by the 1/1 Pade approximant: G(S)≈K 1-0s/2 (rs+1)(1+0s/2) 4口+@4定4定0C Zhang.W.D..CRC Press.2011 Version 1.0 3/78
Section 5.1 H2 PID Controllers for the First-Order Plant 5.1 H2 PID Controllers for the First-Order Plant An analog of H∞ optimal control theory: H2 optimal control theory Assume that the plant is G(s) = Ke−θs τ s + 1 Using the Youla parameterization, we have C(s) = Q(s) 1 − G(s)Q(s) where Q(s) is a stable transfer function. It is difficult to treat e −θs analytically. Approximate it by the 1/1 Pade approximant: G(s) ≈ K 1 − θs/2 (τ s + 1)(1 + θs/2) Zhang, W.D., CRC Press, 2011 Version 1.0 3/78
Section 5.1 H2 PID Controllers for the First-Order Plant The design procedure for the H2 PID controller is similar to that for the Hoo PID controller.The controller is first designed for the approximate plant and then used to control the original plant The H2 optimal index is minW(s)s(s)2 where W(s)is the weighting function.Assume that the system input is a unit step.In view of the discussion in Section 3.2,the weighting function in H2 optimal control should be chosen so that the input is normalized to an impulse,that is,d(s)/W(s)=1. Then,W(s)=1/s. W(s)has a pole on the imaginary axis.To guarantee a finite 2-norm and to have the asymptotic property.a constraint has to be imposed on the design lim S(s)=lim 1-G(s)Q(s=0 40 540 4口,+@,4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 4/78
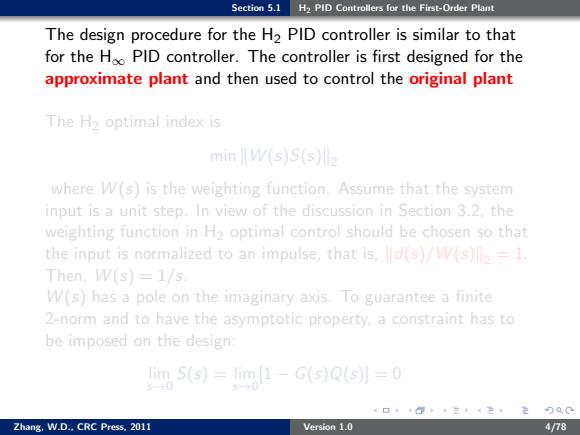
Section 5.1 H2 PID Controllers for the First-Order Plant The design procedure for the H2 PID controller is similar to that for the H∞ PID controller. The controller is first designed for the approximate plant and then used to control the original plant The H2 optimal index is min kW (s)S(s)k2 where W (s) is the weighting function. Assume that the system input is a unit step. In view of the discussion in Section 3.2, the weighting function in H2 optimal control should be chosen so that the input is normalized to an impulse, that is, kd(s)/W (s)k2 = 1. Then, W (s) = 1/s. W (s) has a pole on the imaginary axis. To guarantee a finite 2-norm and to have the asymptotic property, a constraint has to be imposed on the design: lim s→0 S(s) = lim s→0 [1 − G(s)Q(s)] = 0 Zhang, W.D., CRC Press, 2011 Version 1.0 4/78

Section 5.1 H2 PID Controllers for the First-Order Plant The design procedure for the H2 PID controller is similar to that for the Hoo PID controller.The controller is first designed for the approximate plant and then used to control the original plant The H2 optimal index is min llW(s)S(s)ll2 where W(s)is the weighting function.Assume that the system input is a unit step.In view of the discussion in Section 3.2,the weighting function in H2 optimal control should be chosen so that the input is normalized to an impulse,that is,ld(s)/W(s)2=1. Then,W(s)=1/s. W(s)has a pole on the imaginary axis.To guarantee a finite 2-norm and to have the asymptotic property,a constraint has to be imposed on the design: lim S(s)=lim[1-G(s)Q(s)]=0 s→0 5→0 4口,+心4定4生定分QC Zhang.W.D..CRC Press.2011 Version 1.0 4/78
Section 5.1 H2 PID Controllers for the First-Order Plant The design procedure for the H2 PID controller is similar to that for the H∞ PID controller. The controller is first designed for the approximate plant and then used to control the original plant The H2 optimal index is min kW (s)S(s)k2 where W (s) is the weighting function. Assume that the system input is a unit step. In view of the discussion in Section 3.2, the weighting function in H2 optimal control should be chosen so that the input is normalized to an impulse, that is, kd(s)/W (s)k2 = 1. Then, W (s) = 1/s. W (s) has a pole on the imaginary axis. To guarantee a finite 2-norm and to have the asymptotic property, a constraint has to be imposed on the design: lim s→0 S(s) = lim s→0 [1 − G(s)Q(s)] = 0 Zhang, W.D., CRC Press, 2011 Version 1.0 4/78