
§3.2分析方法 3.1支路电流法(branch current method) 2b法- 设电路有b条支路和n个结点, 未知量:各支路电压U和支路电流L共2b个未知量 可列方 独立的KVL方程∑U=0(b-n+1个) 程: 独立的KCL方程:∑k=0 (n-1个) 共2b个 方程 支路的VCR方程数:Uk=f(Ik) b个 所列方程数与未知量数相等。 可由以上2b个方程解出2b个支路电压U和支路电流Lk。 这种方法称为2b法。 2b法方程数太多,解题过程太复杂繁琐,所以很少用
§3.2分析方法 可由以上2b个方程解出2b个支路电压Uk和支路电流Ik 。 这种方法称为2b法。 2b法- 未知量:各支路电压Uk和支路电流Ik 共2b个 方程 设电路有b条支路和n个结点, 共2b个未知量 所列方程数与未知量数相等。 可列方 程: 2b法方程数太多,解题过程太复杂繁琐,所以很少用。 独立的KVL方程 Uk = 0 (b-n+1个) 独立的KCL方程: Ik = 0 (n-1个) 支路的VCR方程数: Uk = f (Ik) b个 3.1 支路电流法 (branch current method )

支路电流法一一一-以各支路电流为未知量列写电路方程分析 电路的方法。 设电路有b条支路和n个结点, 未知量:各支路电流Lk共b个未知量 支路电压U通过支路的VCR方程U=f()用支路电流L 表示,然后代人KVL方程∑Uk=0得:∑fI=0 可列方独立的KVL方程∑f=0(b-n+1个) 共b个 程: 独立的KCL方程∑1=0(n-1个) 方程 所列方程数与未知量数相等。 可由以上b个方程解出b个支路电流L。再根据各支路的VCR方程求 出各支路电压Uk,这种方法称为支路电流法
可由以上b个方程解出b个支路电流Ik 。再根据各支路的VCR方程求 出各支路电压Uk,这种方法称为支路电流法。 支路电流法-以各支路电流为未知量列写电路方程分析 电路的方法。 未知量:各支路电流Ik 共b个 方程 设电路有b条支路和n个结点, 共b个未知量 所列方程数与未知量数相等。 可列方 程: 支路电压Uk通过支路的VCR方程 用支路电流Ik 表示,然后代人KVL方程 得: Uk = f (Ik) Uk = 0 f (Ik ) = 0 独立的KVL方程 (b-n+1个) 独立的KCL方程 (n-1个) f (Ik ) = 0 Ik = 0
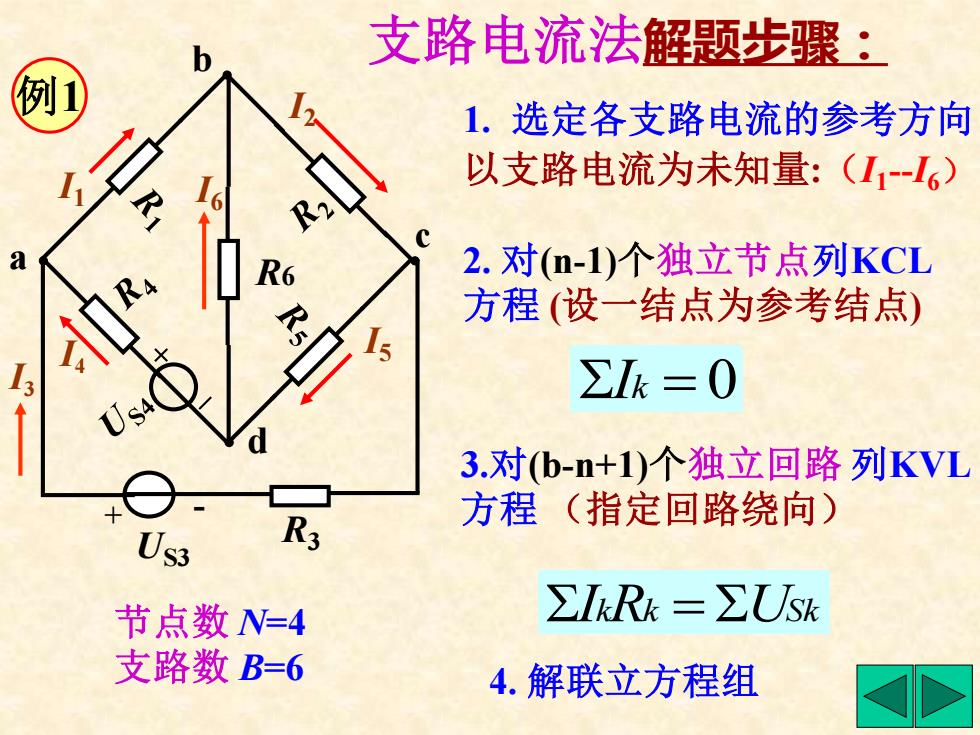
支路电流法解题步骤: 例 1.选定各支路电流的参考方向 以支路电流为未知量:(I1-6) a 2.对(m-1)个独立节点列KCL 方程(设一结点为参考结点) ∑Ik=0 3.对(b-n+1)个独立回路列KVL 方程(指定回路绕向) 0s3 R3 节点数N=4 ∑IkRk=∑USk 支路数B=6 4.解联立方程组
支路电流法解题步骤: 1. 选定各支路电流的参考方向 以支路电流为未知量:(I1 -I6) 4. 解联立方程组 Ik = 0 2. 对(n-1)个独立节点列KCL 方程 (设一结点为参考结点) IkRk = USk 3.对(b-n+1)个独立回路 列KVL 方程 (指定回路绕向) 例1 节点数 N=4 支路数 B=6 US3 + - R3 R6 I2 I5 I6 I1 I4 I3 a b c d
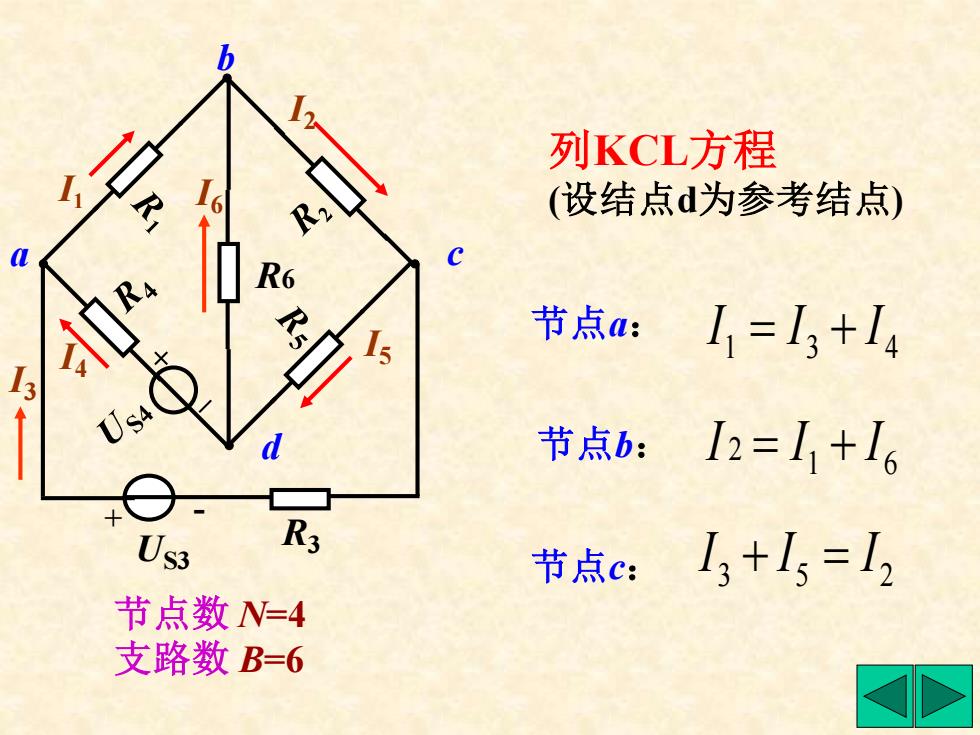
列KCL方程 (设结点d为参考结点) 节点a:11=13+14 节点:I2=11+16 R3 节点c:13+15=I2 节点数N=4 支路数B=6
节点a: 1 3 4 I = I + I 列KCL方程 (设结点d为参考结点) b a c d 节点数 N=4 支路数 B=6 US3 + - R3 R6 I2 I5 I6 I1 I4 I3 节点b: 1 6 I 2 = I + I 节点c: 3 5 2 I + I = I
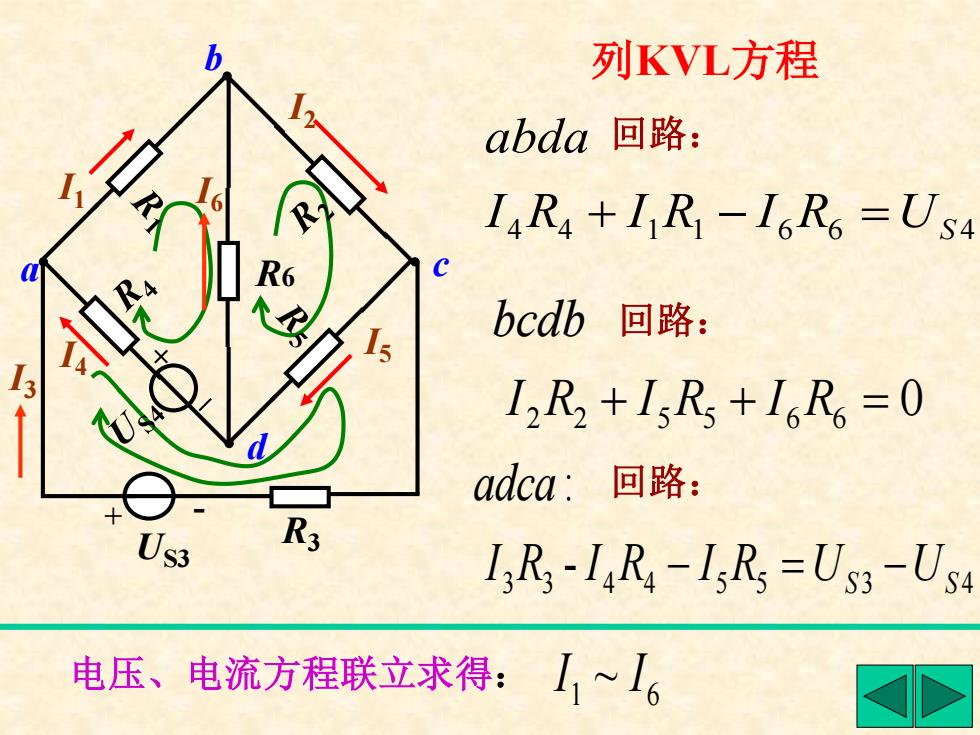
列KVL方程 abda回路: IRa+I R-16R6 =US4 bcdb回路: 12R +IsRs+16R6=0 adca:回路: 03 R3 I3Rs-14R4-IsRs =US3-US 电压、电流方程联立求得:1,~6
列KVL方程 电压、电流方程联立求得: 1 6 I ~ I b a c d 3 3 4 4 5 5 3 4 - : R US US I R I R I adca − = − 0 I 2 R2 + I 5 R5 + I 6 R6 = bcdb 4 4 1 1 6 6 4 R US I R I R I abda + − = US3 + - R3 R6 I2 I5 I6 I1 I4 I3 回路: 回路: 回路: