#3 b 基尔霍夫电流方程: 基尔霍夫电压方程: 节点m:1+I2=I3 #1Us1=1R+13R #2Us2=12R2+3R 节点b:I3=1+2 #3Us1-Us2=1R-12R, 独立方程只有1个 独立方程只有2有
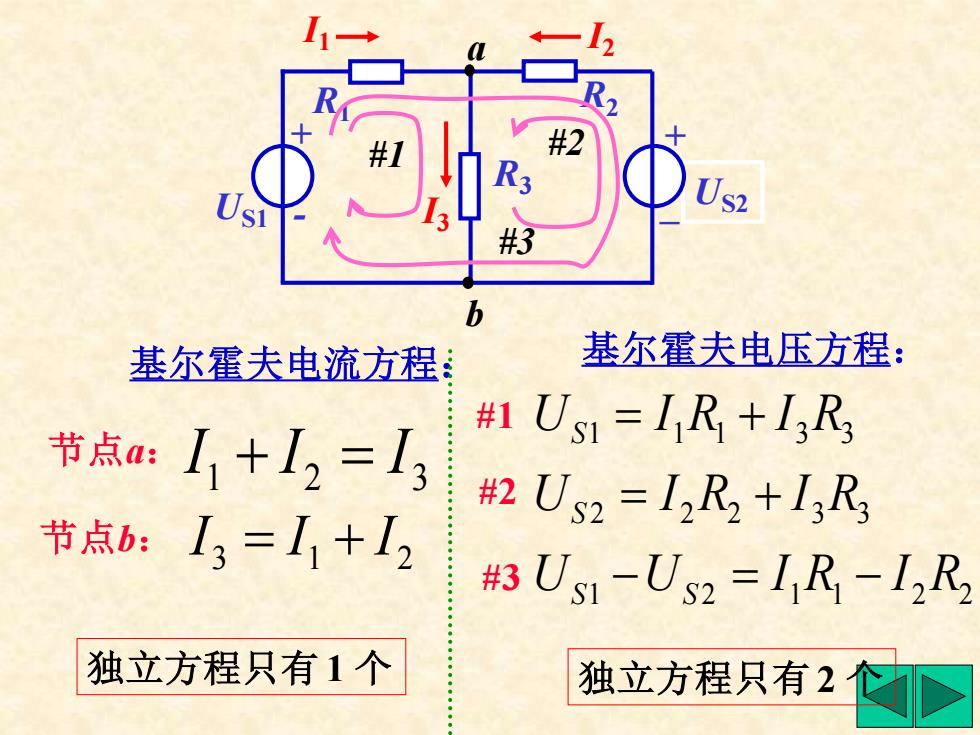
基尔霍夫电流方程: 节点a: 节点b: 1 2 3 I + I = I 3 1 2 I = I + I 独立方程只有 1 个 基尔霍夫电压方程: #1 #2 #3 1 2 1 1 2 2 2 2 2 3 3 1 1 1 3 3 U U I R I R U I R I R U I R I R S S S S − = − = + = + 独立方程只有 2 个 a I1 I2 US2 + - R1 R3 R2 + I _ 3 #1 #2 #3 b US1

几个基本概念: 图G的路径-从图G的某一结点出发,沿着一些支路移 动,到达另一结点,所经过的一系列支路 闭合路径-从图的某一结点出发,沿着一些支路移动, 回到原出发点,所经过的一系列支路 连通图-图G的任两结点间至少存在一条路径 树T-是连通图G的一个连通子图,它包含G的全部结点 ,但不形成回路。 (设图G有n个结点,b条支路) 树支-组成树的支路,共有n-1个。 连支-连通图G除树支外的其他支路,共有b一门+1个
几个基本概念: 图G的路径-从图G的某一结点出发,沿着一些支路移 动,到达另一结点,所经过的一系列支路 闭合路径-从图的某一结点出发,沿着一些支路移动, 回到原出发点,所经过的一系列支路 连通图-图G的任两结点间至少存在一条路径 树T-是连通图G的一个连通子图,它包含G的全部结点 ,但不形成回路。 树支-组成树的支路,共有n-1个。 连支-连通图G除树支外的其他支路,共有b-n+1个。 ( 设图G有n个结点, b条支路)
连通图G 树1 树2 d 树3 树4 树5 a
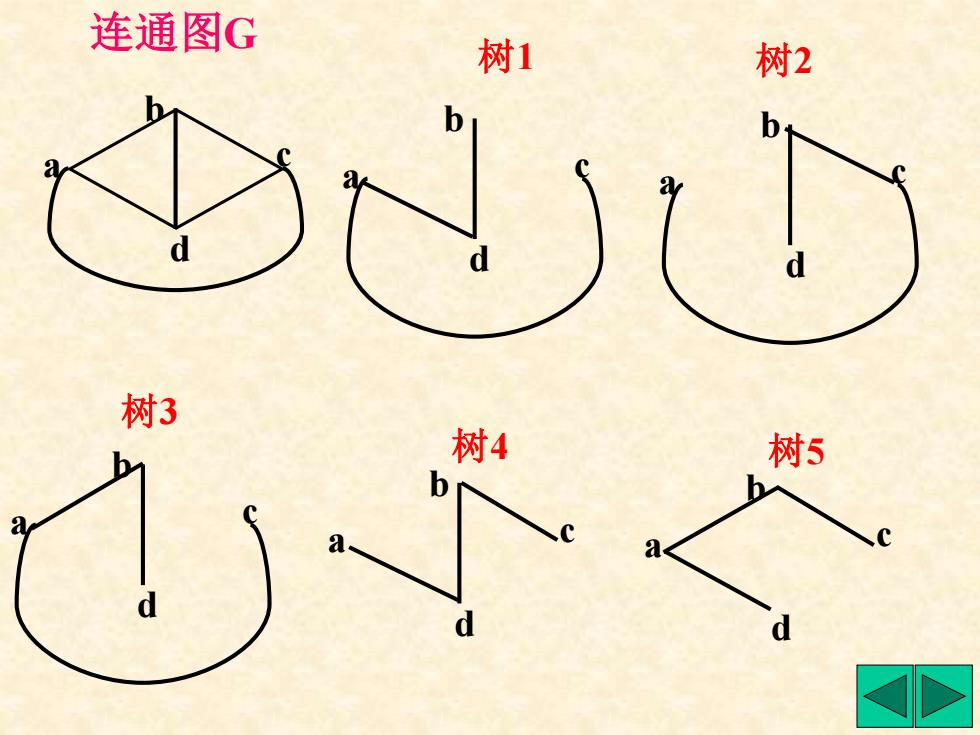
连通图 G a b c d 树 1 a b c d a b c d 树2 树 3 a b c d 树 4 a b c d 树 5 a b c d
连通图G 树T 单连支回路 d d#3 单连支回路(基本回路)-每一个基本回路仅含一个连 支,且这一连支并不出现在其他基本回路中。 单连支回路(基本回路)互相独立 KVL的独立方程数=连支数(b-n+1) KCL的独立方程数=树支数(n-1) 平面图的全部网孔是一组独立回路, 所以平面图的网孔数即独立回路数
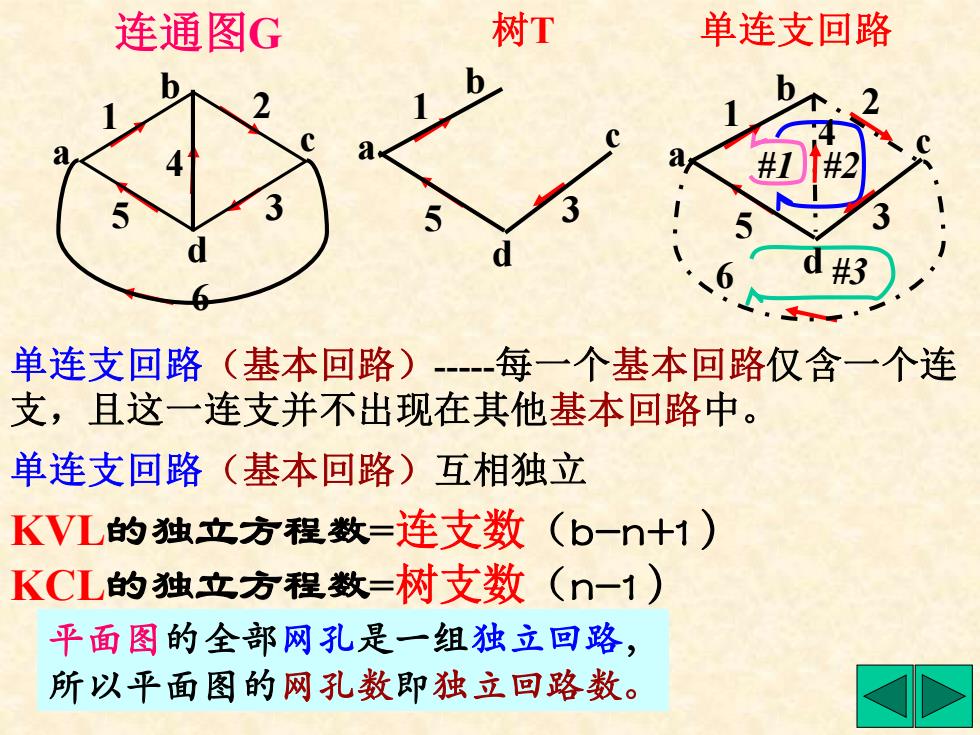
连通图G a b c d 1 2 3 4 5 6 单连支回路(基本回路)-每一个基本回路仅含一个连 支,且这一连支并不出现在其他基本回路中。 KVL的独立方程数=连支数(b-n+1) KCL的独立方程数=树支数(n-1) 单连支回路(基本回路)互相独立 平面图的全部网孔是一组独立回路, 所以平面图的网孔数即独立回路数。 树T a b c d 1 5 3 单连支回路 #1 #2 #3 2 4 6 a b c d 1 5 3
平面电路:可以画在平面上,不出现支路交叉的电路。 非平面电路:在平面上无论将电路怎样画,总有支 路相互交叉。 → ∴。是平面电路 平面电路KVL的独立方程数=网孔数(b-n+1) 总有支路相互交叉 是非平面电路
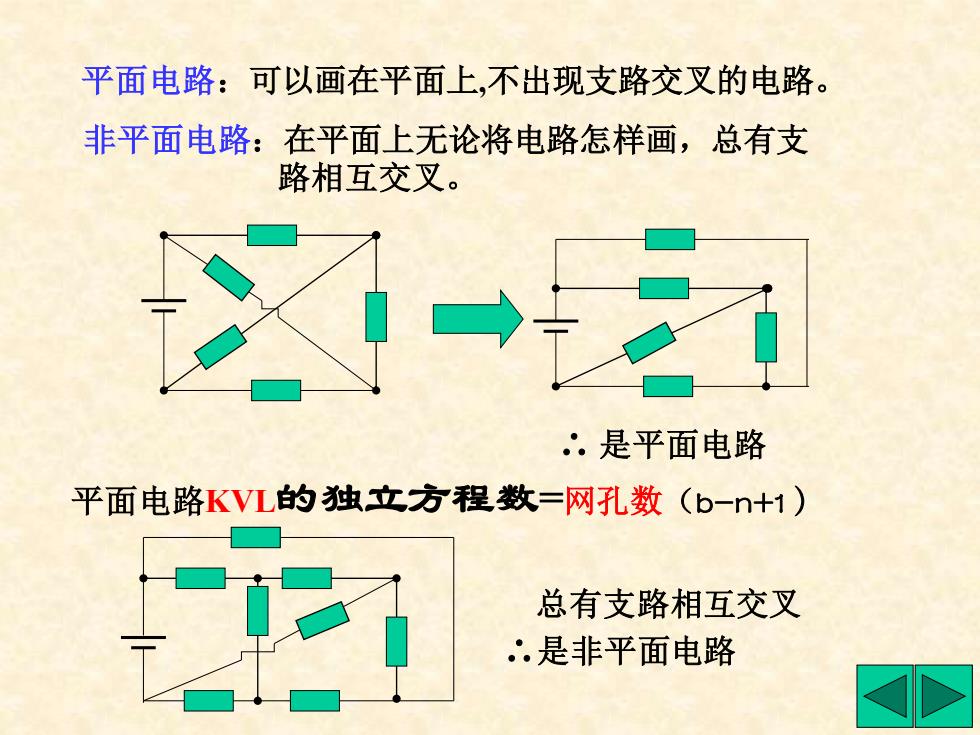
平面电路:可以画在平面上,不出现支路交叉的电路。 非平面电路:在平面上无论将电路怎样画,总有支 路相互交叉。 ∴ 是平面电路 总有支路相互交叉 ∴是非平面电路 平面电路KVL的独立方程数=网孔数(b-n+1)