
0t<0例1求单位阶跃函复挣数的拉t>0数·根据拉氏变换的定义,有这个积分在)=d时收毁,而且有+81+8-ste-stdt =-e二JosS101所以 L[u(t)](Re(s) > 0)Su
6 例1 求单位阶跃函 数 0 0 ( ) 1 0 t u t t = 的拉氏变换. 0 [ ( )] e dst u t t + − = L • 根据拉氏变换的定义, 有 这个积分在Re(s)>0时收敛, 而且有 0 1 1 e d e 0 st st t s s + − − + = − = 1 [ ( )] (Re( ) 0). u t s s 所以 L =

例2求指数函数,f()=e kt的拉氏变换(k为实数).根据拉氏变换的定义,有-Oe-(s-k)tdtC[f(t)]= Teae-stdt=0。这个积分在Re(s)>k时收敛,而且有1180e-(s-k)tf0 e-(s-k)tdt=s-ks-k所以 L[ek]=(Re(s) >k)S-k其实为复数时上式也成立,只是收敛区间为uRe(s)>Re(k)
7 例2 求指数函数 f (t)=e kt 的拉氏变换(k 为实数). ( ) 0 0 [ ( )] e e d e d kt st s k t f t t t + + − − − = = L ( ) ( ) 0 0 1 1 e d e s k t s k t t s k s k + + − − − − = − = − − • 这个积分在Re(s)>k时收敛, 而且有 其实k为复数时上式也成立, 只是收敛区间为 Re(s)>Re(k) 1 [e ] (Re( ) ). kt s k s k = − 所以 L 根据拉氏变换的定义, 有

(1)在t≥0的任一有限区间上分段连续;(2)当t>+8时,f(t)的增长速度不超过某一指数函数,即存在常数M>0及c≥0.使得If (t)|≤ M e ct, 0≤ t <+80F(则)的拉氏变换在半平面Re(s)>c上一定存在,并且在Re(s)> c的半平面内,F(s)为解析函数u
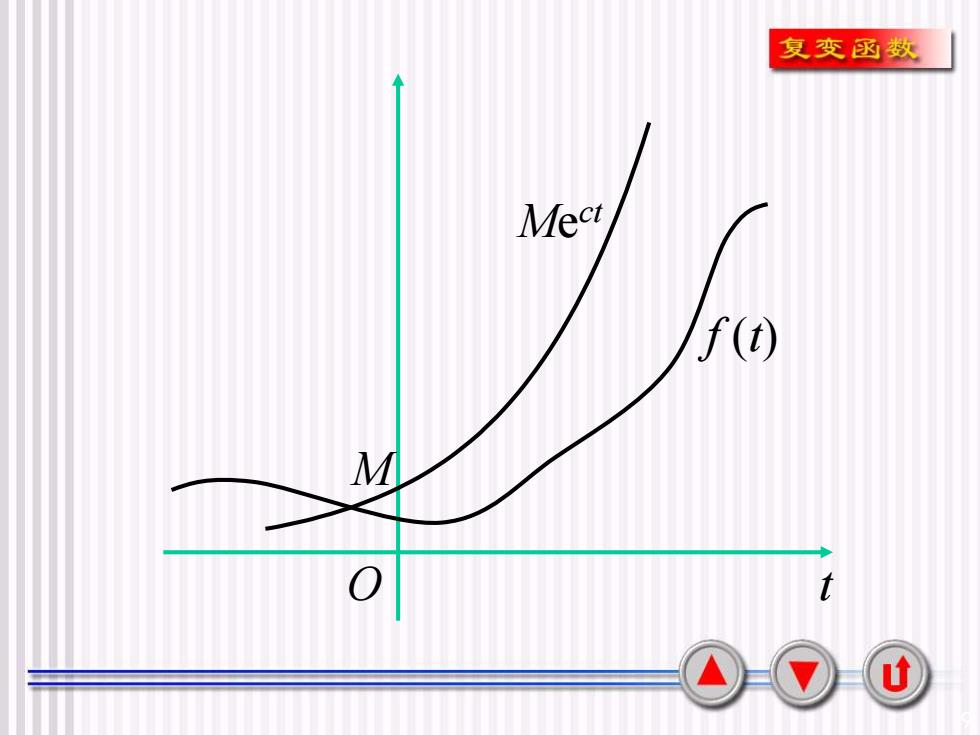
8 2.拉氏变换的存在定理 若函数f (t)满足: (1) 在t 0的任一有限区间上分段连续; (2) 当t→+时, f (t)的增长速度不超过某 一指数函数, 即存在常数 M > 0及c 0, 使得 |f (t)| M e ct, 0 t <+ ( ) ( )e d 则 f 0 (t)的拉氏变换 st F s f t t + − = • 在半平面Re(s)>c上一定存在, 并且在Re(s) > c的半平 面内, F(s)为解析函数
复变函数Mectf(t)M0U
9 M Me ct f (t) O t

(0≤t<+8),有复变函数 f(t)e st |=L f (t)le-βt≤ Me-(β-c)tRe(s)=β,若令β-C≥>0(即β≥C+=所以[("ed=MC注l:大部分常用函数(a变换都存在(常义下)注2:存在定理的条件是充分但非必要条件u
10 说明:由条件2可知, 对于任何t值 (0t<+), 有 | f (t)e st |=| f (t)|e−t Me −(−c)t , Re(s)=, 若令−c e >0 (即 c+e = c1>c), 则 | f (t)e−st| Me −et . 0 0 ( )e d e d . st t M f t t M t e e + + − − = 所以 注1:大部分常用函数的Laplace变换都存在(常义下); 注2:存在定理的条件是充分但非必要条件