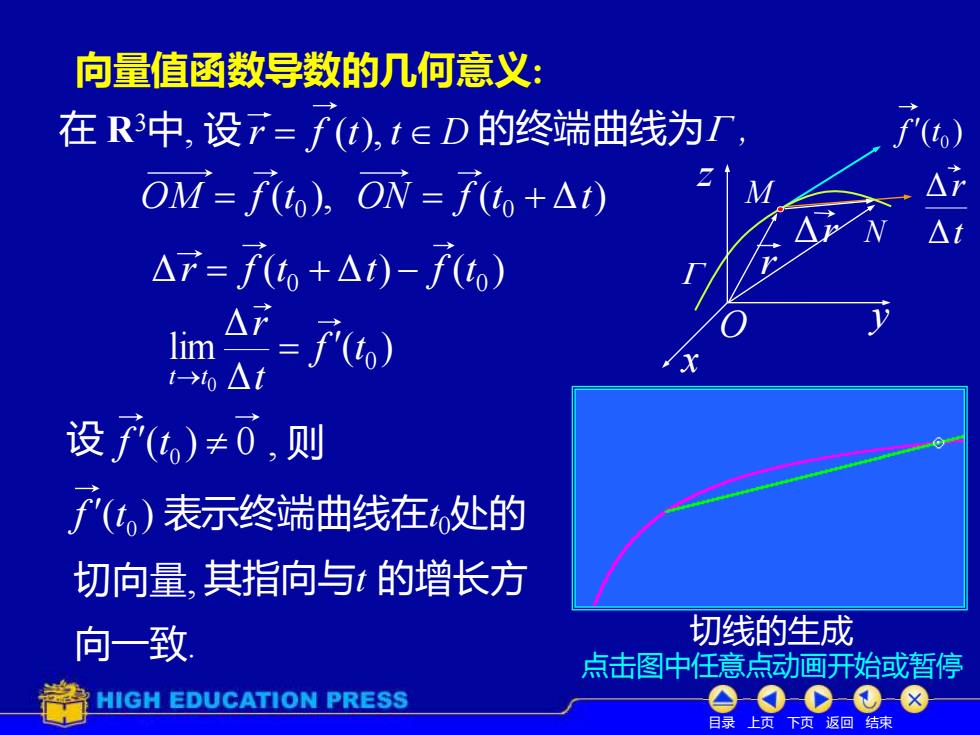
向量值函数导数的几何意义: 在R中,设7=f(d),t∈D的终端曲线为I, t OM=f),ON=f。+△) △T=f。+△)-f,) lim =F() →0△t 设f()≠0,则 f(,)表示终端曲线在处的 切向量,其指向与t的增长方 向一致 切线的生成 点击图中任意点动画开始或暂停 HIGH EDUCATION PRESS eOC①8 目录上页下页返回结束
目录 上页 下页 返回 结束 向量值函数导数的几何意义: 在 R3中, 设 r = f (t), t D 的终端曲线为 , 切线的生成 点击图中任意点动画开始或暂停 M x z O y Δr ( )0 f t t r Δ Δ ( ), ( Δ ) 0 0 OM = f t ON = f t + t N Δ ( Δ ) ( ) 0 0 r = f t + t − f t ( ) Δ Δ lim 0 0 f t t r t t = → 表示终端曲线在t0处的 切向量, 其指向与t 的增长方 向一致. ( )0 f t 设 f (t 0 ) 0 , 则 r

向量值函数导数的物理意义: 设亓=f(1)表示质点沿光滑曲线运动的位置向量,则有 速度向量:0=f) 加速度向量:a=(0)=() 例1.设f)=(cos)i+(sin)j+1k,求1imf) 解:limf()=(lim cos)i+(imsin)j+limt无 7+2+e) HIGH EDUCATION PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 向量值函数导数的物理意义: 设 r = f (t) 表示质点沿光滑曲线运动的位置向量, 则有 v(t) = f (t) a = v (t) = f (t) ( ) (cos ) (sin ) , lim ( ). 4 π f t t i t j t k f t t→ 例1. 设 = + + 求 速度向量: 加速度向量: 解: f t t i t j t k t t t t 4 π 4 π 4 π 4 π lim ( ) (lim cos ) (limsin ) lim → → → → = + + i j k 4 π 2 2 2 2 = + + ( ( ) ) 4 π = f

例2.设空间曲线厂的向量方程为 7=ft)=(2+1,4t-3,2-6),1∈R 求曲线T上对应于1。=2的点处的单位切向量 解:f"()=(2i,4,4t-6),teR f'(2)=(4,4,2) 7(2)=V42+42+22=6 故所求单位切向量为 其方向与t的增长方向一致 另一与1的增长方向相反的单位切向量为(-?-乙 HIGH EDUCATION PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例2. 设空间曲线 的向量方程为 求曲线 上对应于 解: ( ) ( 1, 4 3, 2 6 ) 2 2 r = f t = t + t − t − t 的点处的单位切向量. 故所求单位切向量为 其方向与 t 的增长方向一致 另一与 t 的增长方向相反的单位切向量为 ) 3 1 , 3 2 , 3 2 (− − −

例3.一人悬挂在滑翔机上,受快速上升气流影响作螺 旋式上升,其位置向量为7=(3cost,3simt,t),求 (1)滑翔机在任意时垓刻t的速度向量与加速度向量 (2)滑翔机在任意时刻1的速率 (3)滑翔机的加速度与速度正交的时刻 解:(1)下=7(t)=(-3sint,3c0s1,20 a==(-3cost,-3sint,2) (2) r(t)=V(3sin)2+(-3cos)2+(2r)2=9+4 (3)由v.a=0即9 sintcost-9 costsint+4t=0, 得t=0,即仅在开始时该刻滑翔机的加速度与速度正交 HIGH EDUCATION PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例3. 一人悬挂在滑翔机上, 受快速上升气流影响作螺 旋式上升, 其位置向量为 求 (1) 滑翔机在任意时刻 t 的速度向量与加速度向量; (2) 滑翔机在任意时刻 t 的速率; (3) 滑翔机的加速度与速度正交的时刻. 解: (1) (3) 由 即 得t = 0, 即仅在开始时刻滑翔机的加速度与速度正交

二、空间曲线的切线与法平面 空间光滑曲线在点M处的切线为此点处割线的极限位 置、过点M与切线垂直的平面称为曲线在该点的法平面. 给定光滑曲线 I:f(t)=(p(t),w(t),@(t)) 则当o,wo'不同时为0时,T在 点M(化,yz)处的切向量及法平面的 法向量均为 f'(1)=(0'(),W(1),o'(t) 点向式可建立曲线的切线方程 利用 点法式可建立曲线的法平面方程 HIGH EDUCATION PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 二、空间曲线的切线与法平面 过点 M 与切线垂直的平面称为曲线在该点的法平面. T M 置. 空间光滑曲线在点 M 处的切线为此点处割线的极限位 :f (t) = ((t), (t),(t)) 给定光滑曲线 在 f (t) = ((t),(t),(t)) 点法式可建立曲线的法平面方程 利用 则当 , ,不同时为 0时, 点M (x, y, z) 处的切向量及法平面的 法向量均为 点向式可建立曲线的切线方程