
第1章命题逻辑 (pVq),(pVq),(p-(pvq)), (p→q)∧(q→r)(S→) 下列符号串不是合式公式: (p→q)→(∧q),(p→q,(pΛq)→q) 定义1.2.1给出合式公式定义的方法称为归纳定义,它包 括三部分:基础,归纳和界限。定义1.2.1中的1)是基础,(2) 和(3)是归纳,(4)是界限。下文中还将多次出现这种形式的定 义。 为方便起见,对命题公式约定如下: (1)最外层括号可以省略。 (2)规定联结词的优先级由高到低依次为,∧,V, →。按此优先级别,如果去掉括号,不改变原公式运算次序 也可以省掉这些括号 般地说,命题公式中包含命题变元,因而无法计算其 真值,所以不是命题。 命题公式中的命题变元,也叫命题公式的分量
第1章 命题逻辑 ¬(p∨q),¬(p∨q),(p→(p∨¬q)), (((p→q)∧(q→r))↔(s↔t)) 下列符号串不是合式公式: (p→q)→(∧q),(p→q,(p∧q)→q) 定义1.2.1给出合式公式定义的方法称为归纳定义,它包 括三部分:基础,归纳和界限。定义1.2.1中的⑴是基础,⑵ 和⑶是归纳,⑷是界限。下文中还将多次出现这种形式的定 义。 为方便起见,对命题公式约定如下: ⑴最外层括号可以省略。 ⑵规定联结词的优先级由高到低依次为¬,∧,∨,→, ↔。按此优先级别,如果去掉括号,不改变原公式运算次序, 也可以省掉这些括号。 一般地说,命题公式中包含命题变元,因而无法计算其 真值,所以不是命题。 命题公式中的命题变元,也叫命题公式的分量

第1章命题逻辑 有了命题公式的概念,就可以用命题公式表示复合命 题,常将这个过程称为命题的符号化。命题的符号化可按 如下步骤进行: (1)找出复合命题中的原子命题。 (2)用小写的英文字母或带下标的小写的英文字母表示 这些原子命题 (3)使用命题联结词将这些小写的英文字母或带下标的 小写的英文字母连接起来。 【例1.7】将下列命题符号化: 他或者骑自行车去学校,或者乘公共汽车去学校。 解:令p:他骑自行车去学校。 9: 他乘公共汽车去学校。 此命题中的或是不可兼或,所以不能符号化为:pVq。 而要符号化为:(pq)或(p∧q)V(p∧q)。稍后会看到 这个表示是正确的。 返回章目录
第1章 命题逻辑 有了命题公式的概念,就可以用命题公式表示复合命 题,常将这个过程称为命题的符号化。命题的符号化可按 如下步骤进行: ⑴找出复合命题中的原子命题。 ⑵用小写的英文字母或带下标的小写的英文字母表示 这些原子命题。 ⑶使用命题联结词将这些小写的英文字母或带下标的 小写的英文字母连接起来。 【例1.7】将下列命题符号化: 他或者骑自行车去学校,或者乘公共汽车去学校。 解:令 p:他骑自行车去学校。 q:他乘公共汽车去学校。 此命题中的或是不可兼或,所以不能符号化为:p∨q。 而要符号化为:¬(p↔q)或(¬p∧q)∨(p∧¬q)。稍后会看到 这个表示是正确的。 返回章目录

第1章命题逻新 1.3真值表和等价公式 1.3.1命题公式的真值表 定义13.1设p,P2,,Pn是出现在公式4中的全部命题 变元,给p,p2,…,Pn各指定一个真值,称为对公式A的 个赋值或解释。若指定的赋值使A的真值为T,则称这个赋值 为A的成真赋值,若使A的真值为F,则称这个赋值为A的成假 赋值。 例如,给公式(pVq→r赋值011是指p=0,q=1,=1,它 是该公式的成真赋值;赋值110是指p=1,q1,=0,它是该 公式的成假赋值。 定义1.3.2在命题公式A中,对A的每一个赋值,就确定了 A的一个真值,把它们汇列成表,称该表为命题公式A的真值 表
第1章 命题逻辑 1.3真值表和等价公式 1.3.1命题公式的真值表 定义1.3.1 设pl,p2,…,pn是出现在公式A中的全部命题 变元,给pl,p2,…,pn各指定一个真值,称为对公式A的一 个赋值或解释。若指定的赋值使A的真值为T,则称这个赋值 为A的成真赋值,若使A的真值为F,则称这个赋值为A的成假 赋值。 例如,给公式(p∨q→r)赋值011是指p=0,q=1,r=1,它 是该公式的成真赋值;赋值110是指p=1,q=1,r=0,它是该 公式的成假赋值。 定义1.3.2 在命题公式A中,对A的每一个赋值,就确定了 A的一个真值,把它们汇列成表,称该表为命题公式A的真值 表
第1章命题逻精 【例1.8】构造命题公式pVg的真值表,并求成真赋 值和成假赋值。 解:命题公式pVg的真值表如表1.6所示。00,01, 11是成真赋值,10是成假赋值。 表1.6 p 9 p pVq 0 0 1 1 0 1 1 1 1 0 0 0 1 0 1
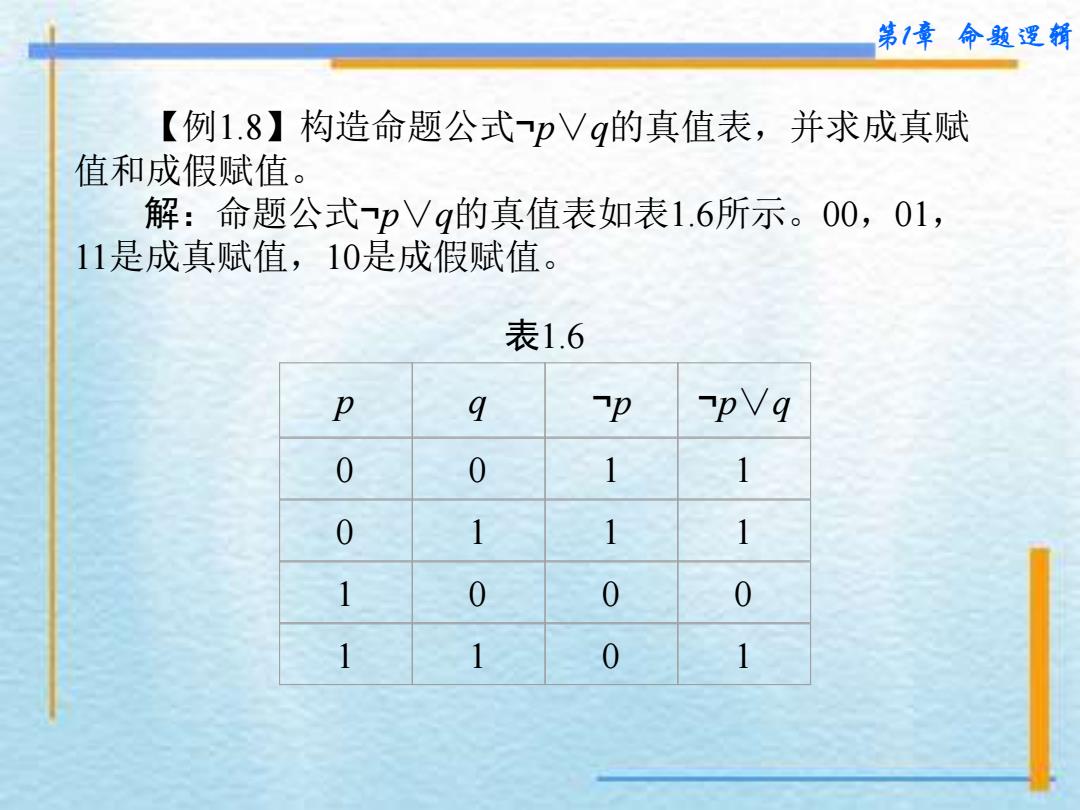
第1章 命题逻辑 【例1.8】构造命题公式¬p∨q的真值表,并求成真赋 值和成假赋值。 解:命题公式¬p∨q的真值表如表1.6所示。00,01, 11是成真赋值,10是成假赋值。 表1.6 p q ¬p ¬p∨q 0 0 1 1 0 1 1 1 1 0 0 0 1 1 0 1
第1章命题逻辑 【例1.9】构造命题公式(p个q)V(一p∧q)的真值表,并 求成真赋值和成假赋值。 解:命题公式(p∧q)V(p∧q)的真值表如表1.7所示。 00,11是成真赋值,01,10是成假赋值。 表1.7 p p∧q p qpΛq(p∧q)V(p∧q 0 1 1 1 1 0 1 0 1 0 0 0 1 0 0 0 1 0 0 1 1 1 0 0 0 1
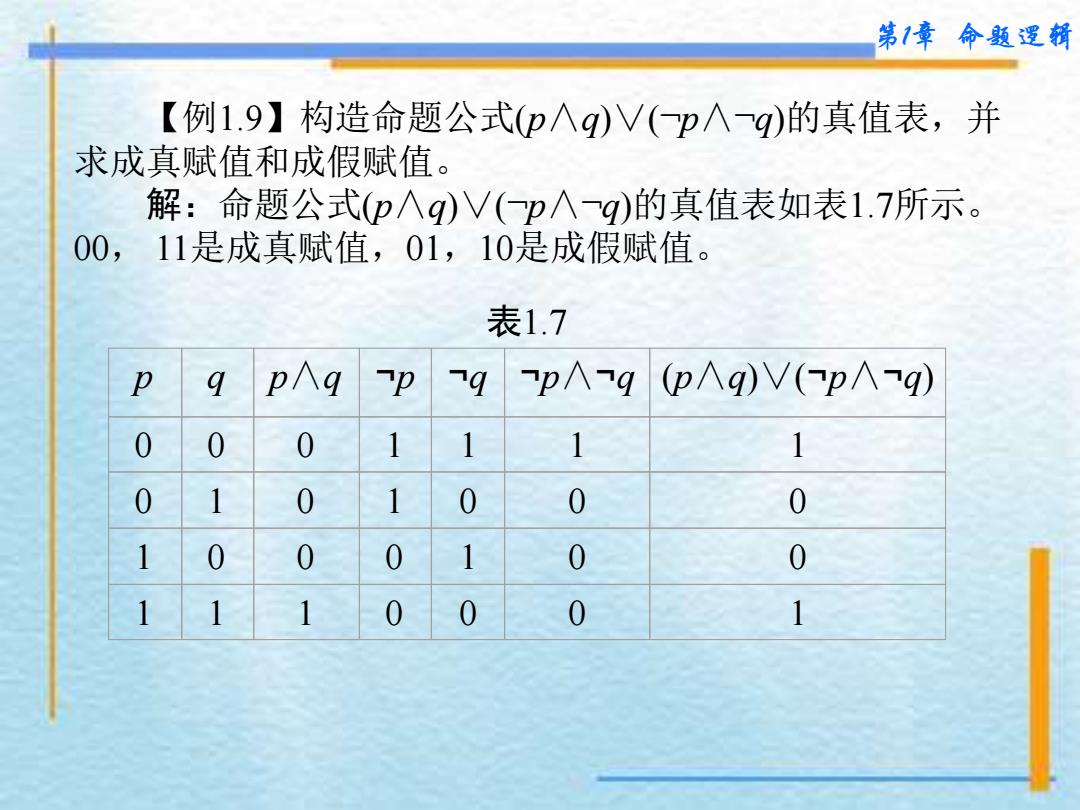
第1章 命题逻辑 表1.7 p q p∧q ¬p ¬q ¬p∧¬q (p∧q)∨(¬p∧¬q) 0 0 0 1 1 1 1 0 1 0 1 0 0 0 1 0 0 0 1 0 0 1 1 1 0 0 0 1 【例1.9】构造命题公式(p∧q)∨(¬p∧¬q)的真值表,并 求成真赋值和成假赋值。 解:命题公式(p∧q)∨(¬p∧¬q)的真值表如表1.7所示。 00, 11是成真赋值,01,10是成假赋值