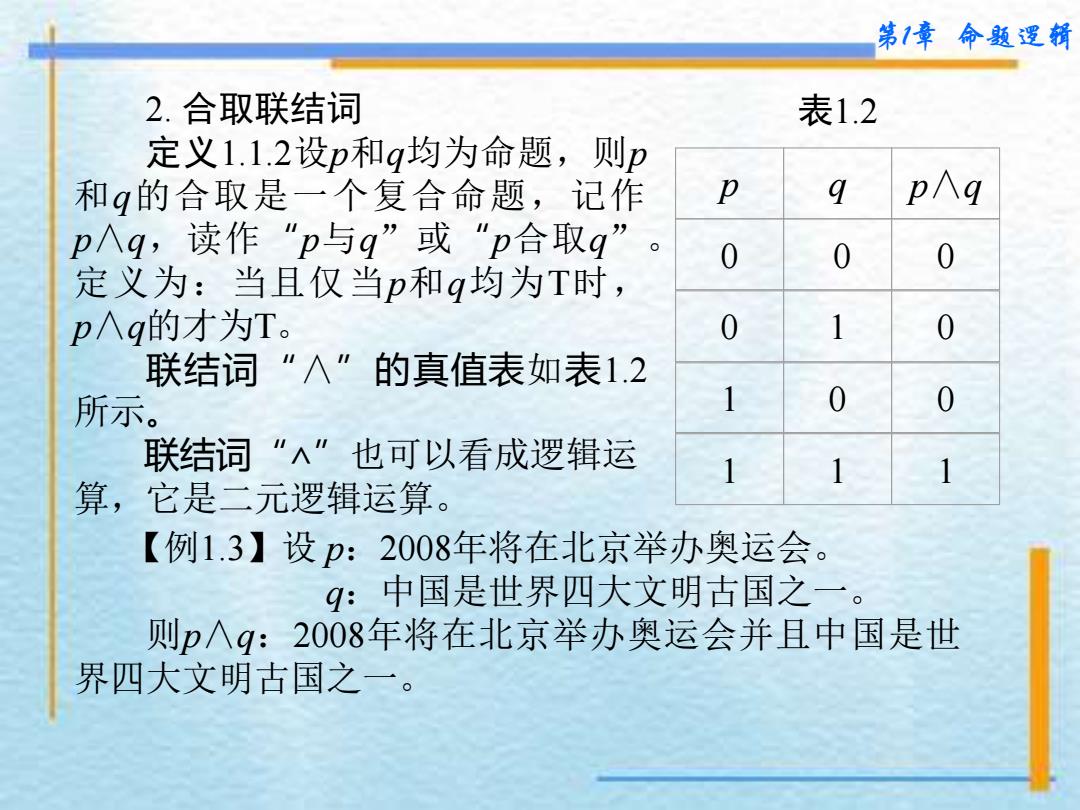
第1章命题逻精 2.合取联结词 表1.2 定义1.1.2设p和g均为命题,则p 和g的合取是一个复合命题,记作 p 9 p∧q p∧q,读作"p与g”或“p合取q 0 0 0 定义为:当且仅当p和g均为T时 p∧g的才为T。 0 1 0 联结词“个”的真值表如表1.2 所示。 1 0 0 联结词“∧”也可以看成逻辑运 1 1 1 算,它是二元逻辑运算。 【例1.3】设p:2008年将在北京举办奥运会。 9:中国是世界四大文明古国之一。 则p个g:2008年将在北京举办奥运会并且中国是世 界四大文明古国之一
第1章 命题逻辑 2. 合取联结词 定义1.1.2设p和q均为命题,则p 和q的合取是一个复合命题,记作 p∧q,读作“ p与q ”或“ p合取q ” 。 定义为:当且仅当p和q均为T时, p∧q的才为T。 联结词“∧”的真值表如表1.2 所示。 联结词“∧”也可以看成逻辑运 算,它是二元逻辑运算。 表1.2 p q p∧q 0 0 0 0 1 0 1 0 0 1 1 1 【例1.3】设 p:2008年将在北京举办奥运会。 q:中国是世界四大文明古国之一。 则p∧q:2008年将在北京举办奥运会并且中国是世 界四大文明古国之一
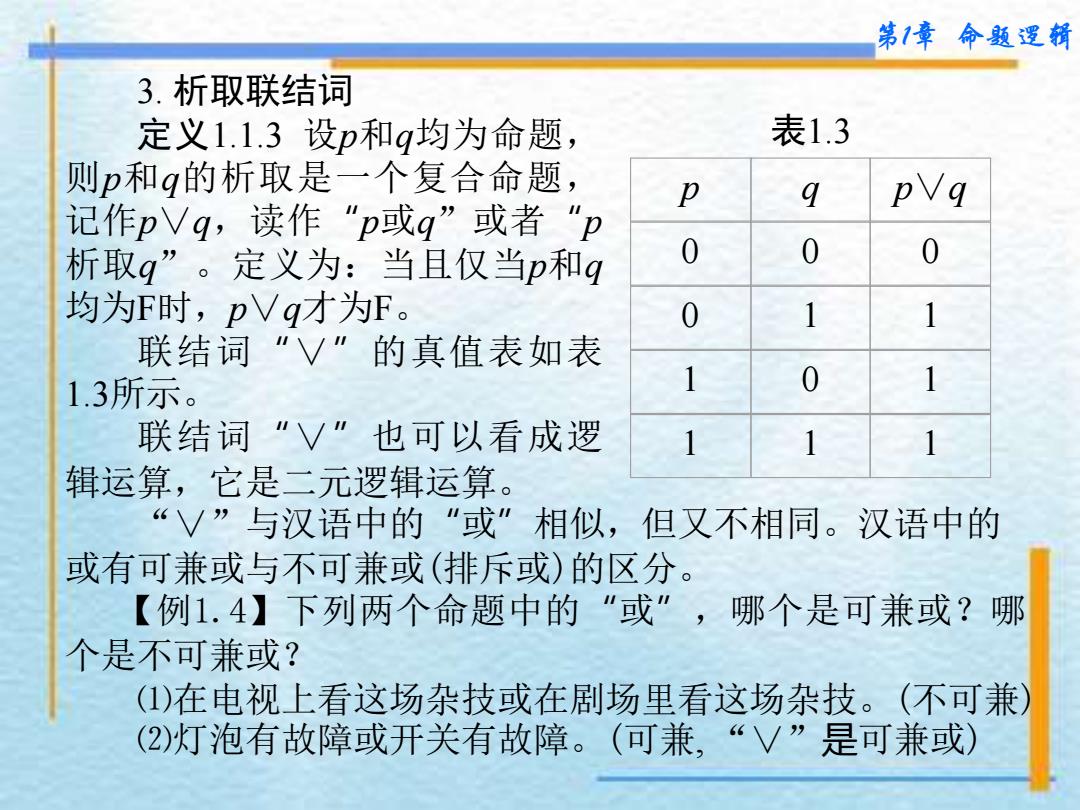
第1章命题逻辑 3.析取联结词 定义1.1.3设p和q均为命题 表1.3 则p和g的析取是一个复合命题 p q pVq 记作pVq,读作"p或q”或者"p 析取g”。定义为:当且仅当p和q 0 0 0 均为F时,pVq才为F。 0 1 1 联结词”V”的真值表如表 1.3所示。 1 0 1 联结词“V”也可以看成逻 1 1 1 辑运算,它是二元逻辑运算。 “V”与汉语中的“或”相似,但又不相同。汉语中的 或有可兼或与不可兼或(排斥或)的区分。 【例1.4】下列两个命题中的“或”,哪个是可兼或?哪 个是不可兼或? (1)在电视上看这场杂技或在剧场里看这场杂技。(不可兼) (2)灯泡有故障或开关有故障。(可兼,“V”是可兼或)
第1章 命题逻辑 3. 析取联结词 定义1.1.3 设p和q均为命题, 则p和q的析取是一个复合命题, 记作p∨q,读作“ p或q ”或者“ p 析取q ” 。定义为:当且仅当p和q 均为F时,p∨q才为F。 联结词“∨”的真值表如表 1.3所示。 联结词“∨”也可以看成逻 辑运算,它是二元逻辑运算。 表1.3 p q p∨q 0 0 0 0 1 1 1 0 1 1 1 1 “∨”与汉语中的“或”相似,但又不相同。汉语中的 或有可兼或与不可兼或(排斥或)的区分。 【例1.4】下列两个命题中的“或” ,哪个是可兼或?哪 个是不可兼或? ⑴在电视上看这场杂技或在剧场里看这场杂技。(不可兼) ⑵灯泡有故障或开关有故障。(可兼, “∨”是可兼或)
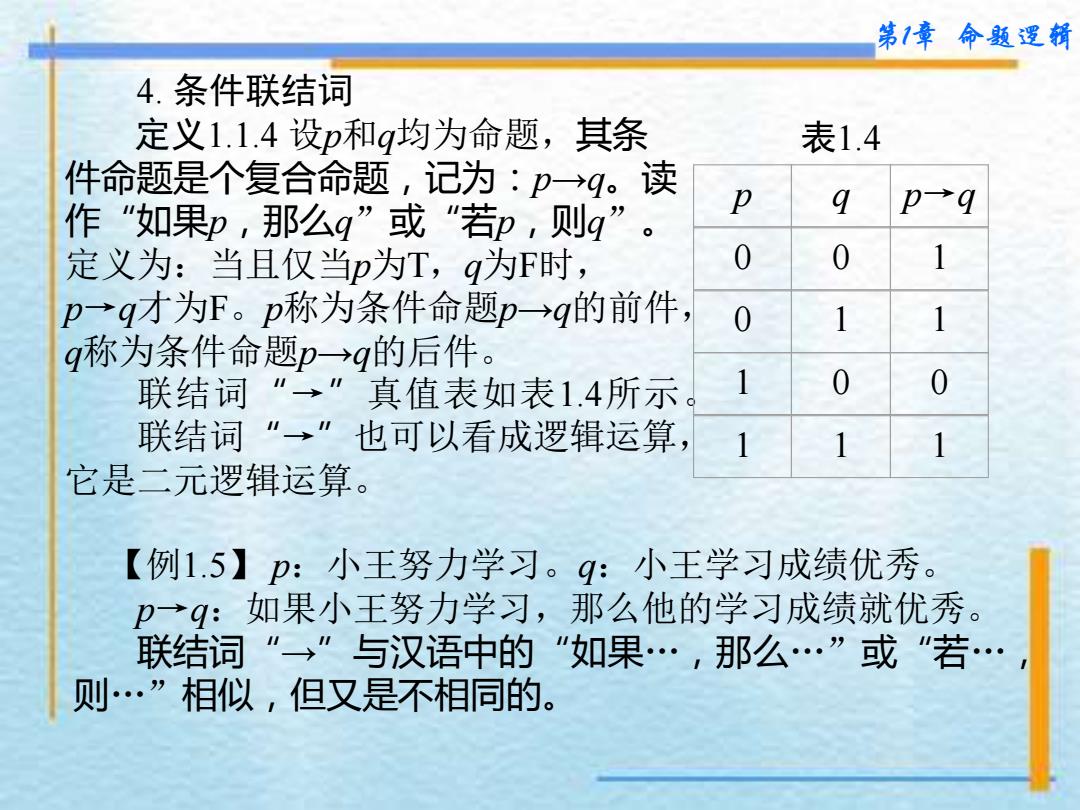
第1章命题逻辑 4.条件联结词 定义1.1.4设p和g均为命题,其条 表1.4 件命题是个复合命题,记为:p→q。读 作”如果p,那么g”或"若,则g”。 q p→q 定义为:当且仅当p为T,q为F时, 0 0 1 p→q才为F。p称为条件命题p→q的前件 0 1 1 q称为条件命题p→9的后件。 联结词 真值表如表1.4所示 1 0 0 联结词”→” 也可以看成逻辑运算, 1 1 1 它是二元逻辑运算。 【例1.5】p:小王努力学习。q:小王学习成绩优秀。 p→9:如果小王努力学习,那么他的学习成绩就优秀。 联结词”→”与汉语中的“如果…,那么…”或“若 则…”相似,但又是不相同的
第1章 命题逻辑 4. 条件联结词 定义1.1.4 设p和q均为命题,其条 件命题是个复合命题,记为:p→q。读 作“如果p,那么q ”或“若p,则q ” 。 定义为:当且仅当p为T,q为F时, p→q才为F。p称为条件命题p→q的前件, q称为条件命题p→q的后件。 联结词“ → ”真值表如表1.4所示。 联结词“ → ”也可以看成逻辑运算, 它是二元逻辑运算。 表1.4 p q p→q 0 0 1 0 1 1 1 0 0 1 1 1 【例1.5】 p:小王努力学习。q:小王学习成绩优秀。 p→q:如果小王努力学习,那么他的学习成绩就优秀。 联结词“ → ”与汉语中的“如果…,那么…”或“若…, 则…”相似,但又是不相同的
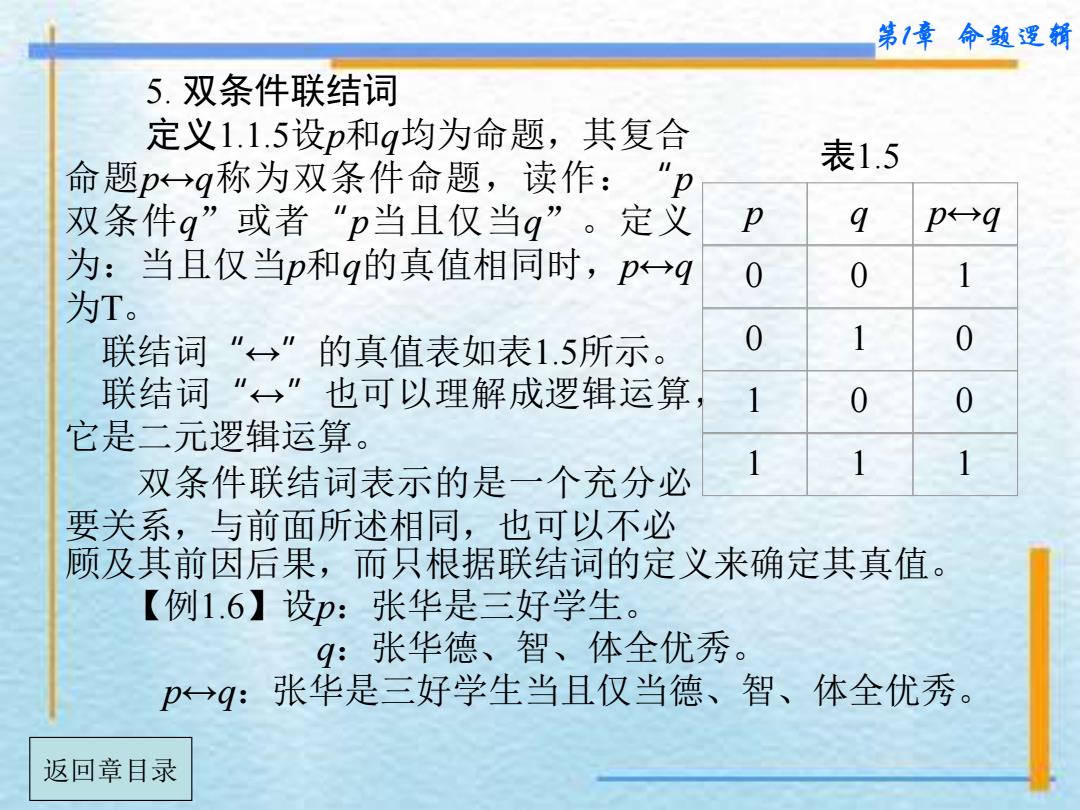
第1章命数逻辑 5.双条件联结词 定义1.1.5设p和g均为命题,其复合 命题p>q称为双条件命题,读作:”p 表1.5 双条件g”或者“p当且仅当g”。定义 卫 9 p→9 为:当且仅当p和q的真值相同时,p→q 0 0 1 为T。 联结词“←→” 的真值表如表1.5所示。 0 1 0 联结词“←→”也可以理解成逻辑运算 1 0 0 它是二元逻辑运算。 双条件联结词表示的是一个充分必 1 1 1 要关系,与前面所述相同,也可以不必 顾及其前因后果,而只根据联结词的定义来确定其真值。 【例1.6】设p:张华是三好学生。 9:张华德、智、体全优秀。 pq:张华是三好学生当且仅当德、智、体全优秀。 返回章目录
第1章 命题逻辑 5. 双条件联结词 定义1.1.5设p和q均为命题,其复合 命题p↔q称为双条件命题,读作:“ p 双条件q ”或者“ p当且仅当q ” 。定义 为:当且仅当p和q的真值相同时,p↔q 为T。 联结词“ ↔ ”的真值表如表1.5所示。 联结词“ ↔ ”也可以理解成逻辑运算, 它是二元逻辑运算。 双条件联结词表示的是一个充分必 要关系,与前面所述相同,也可以不必 表1.5 p q p↔q 0 0 1 0 1 0 1 0 0 1 1 1 顾及其前因后果,而只根据联结词的定义来确定其真值。 【例1.6】设p:张华是三好学生。 q:张华德、智、体全优秀。 p↔q:张华是三好学生当且仅当德、智、体全优秀。 返回章目录

第1章命题逻新 1.2命题公式与翻译 把命题常量,命题变量按照一定的逻辑顺序用命题联结 词连接起来就构成了命题演算的合式公式,也叫命题公式。 当使用联结词集,∧,V,,→时,合式公式定义如下: 定义1.2.1按下列规则构成的符号串称为命题演算的合式 公式,也称为命题公式,简称公式。 (1)单个命题变元和常元是合式公式。 (2)如果A是合式公式,那么A是合式公式。 (3)如果A和B是合式公式,那么(A∧B)、(AVB)、(A→B) 和(A→B)是合式公式。 (4)当且仅当有限次地应用了(1)、(2)、(3)所得到的符号串 是合式公式。 命题公式一般的用大写的英文字母A,B,C,…表示。 依照这个定义,下列符号串是合式公式:
第1章 命题逻辑 1.2 命题公式与翻译 把命题常量,命题变量按照一定的逻辑顺序用命题联结 词连接起来就构成了命题演算的合式公式,也叫命题公式。 当使用联结词集¬,∧,∨,→,↔时,合式公式定义如下: 定义1.2.1按下列规则构成的符号串称为命题演算的合式 公式,也称为命题公式,简称公式。 ⑴单个命题变元和常元是合式公式。 ⑵如果A是合式公式,那么¬A是合式公式。 ⑶如果A和B是合式公式,那么(A∧B)、(A∨B)、(A→B) 和(A↔B)是合式公式。 ⑷当且仅当有限次地应用了⑴、⑵、⑶所得到的符号串 是合式公式。 命题公式一般的用大写的英文字母A,B,C,…表示。 依照这个定义,下列符号串是合式公式: