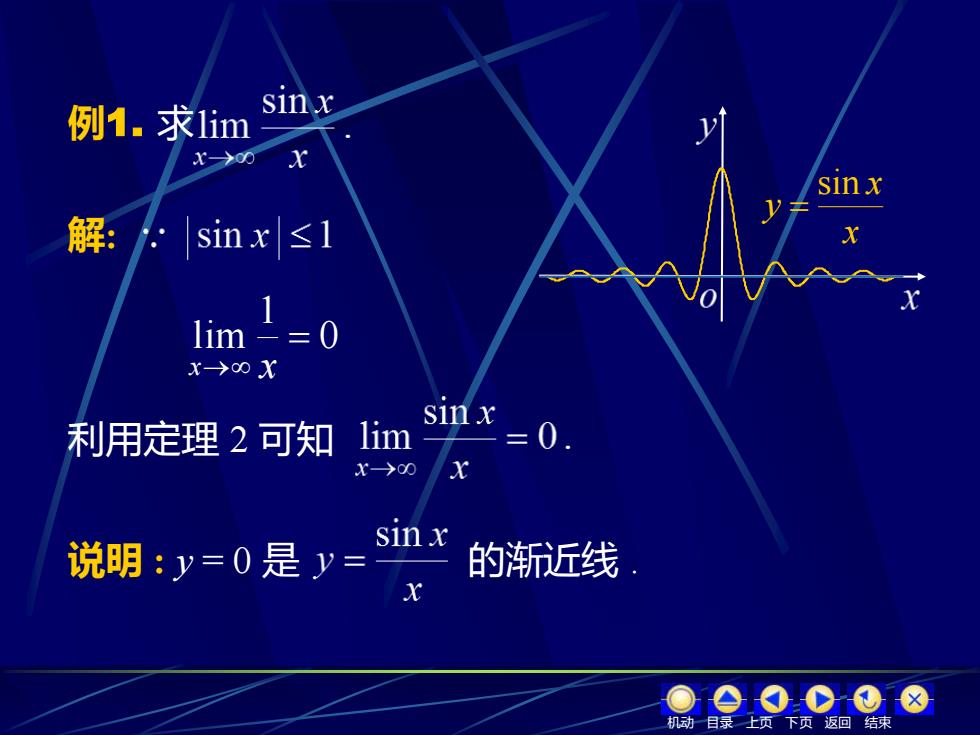
例1.求1im sin x X→00 X sinx 解:sinx≤1 X 1im2=0 x→0X sin x 利用定理2可知 lim =0 X→00 X sin x 说明:y=0是y= 的渐近线 X 机动目录上页下页返回结束
例1. 求 解: 0 1 lim = x→ x 利用定理 2 可知 x x y sin = 说明 : y = 0 是 的渐近线 . 机动 目录 上页 下页 返回 结束

二、极限的四则运算法则 定理3.若1im不(x)=A,limg(x)=B,则有 im[f(x)±gx)]=limf(x)±limg(x)=A±B 证:因limf(x)=A,limg(x)=B,则有 f(x)=A+a,8(x)=B+B (其中x,B为无穷小) 于是 f(x)±g(x)=(A+C)±(B+B) =(A土B)+(C±B) 由定理1可知士阝也是无穷小,再利用极限与无穷小 的关系定理,知定理结论成立 机动目录」 页下页返回结束
二、 极限的四则运算法则 lim f (x) = A, limg(x) = B , 则有 证: 因 lim f (x) = A, limg(x) = B , 则有 f (x) = A+ , g(x) = B + (其中 , 为无穷小) 于是 f (x) g(x) = (A+ ) (B + ) = (A B) + ( ) 由定理 1 可知 也是无穷小, 再利用极限与无穷小 的关系定理 , 知定理结论成立 . 定理 3 . 若 机动 目录 上页 下页 返回 结束

推论:若1imf(x)=A,1img(x)=B,且f(x)≥g(x), 则A≥B.P45定理5) 提示:令p(x)=f(x)-g(x) 利用保号性定理证明 说明:定理3可推广到有限个函数相加、减的情形 机动目录上页下页返回结束
推论: 若 lim f (x) = A, limg(x) = B, 且 f (x) g(x), 则 A B . ( P45 定理 5 ) (x) = f (x) − g(x) 利用保号性定理证明 . 说明: 定理 3 可推广到有限个函数相加、减的情形 . 提示: 令 机动 目录 上页 下页 返回 结束

定理4.若1imf(x)=A,limg(x)=B,则有 lim[f()g(x)]=limf(x)limg(x)=4B 提示:利用极限与无穷小关系定理及本节定理2证明 说明:定理4可推六到有限个函数相乘的情形 推论1.lim[Cf(x)小=Climf(x) (C为常数) 推论2.1im[f(x)]”=[limf(x)] (n为正整数) 例2.设n次多项式P()=a0+a1x++anx”,试证 lim P (x)=P(o). x→X0 证:lim P((x)=ao+a1limx+…+an lim x” x-→X0 x今X0 x→x0 =Pn(xo】 8 机动目录 页下页返回结束
定理 4 . 若 lim f (x) = A, limg(x) = B , 则有 提示: 利用极限与无穷小关系定理及本节定理2 证明 . 说明: 定理 4 可推广到有限个函数相乘的情形 . 推论 1 . lim[C f (x)] = Clim f (x) ( C 为常数 ) 推论 2 . n n lim[ f (x)] = [lim f (x)] ( n 为正整数 ) 例2. 设 n 次多项式 试证 lim ( ) ( ). 0 0 P x P x n n x x = → 证: = → lim ( ) 0 P x n x x 机动 目录 上页 下页 返回 结束