
例6-2-1计算无限长直导线与矩形线圈之间的互感。设线圈与导线平行,周围媒质为真空,如图示。解建立圆柱坐标系,令Z轴方向与电流I一致,则I产生的磁感应强度为ulB,2元r与线圈电流I交链的磁通链,为Y2 = [, B, · dS若线框电流如图所示的顺时针方向,则dS与B方向相同。那么D+bogD+b1.-uolaY,2元JD2元DL
例 6-2-1 计算无限长直导线与矩形线圈之间的互感。 设线圈与导线平行,周围媒质为真空,如图示。 a b dr r D I 0 1 I2 z S2 解 建立圆柱坐标系,令z 轴方向与电 流 I 1一致,则I 1 产生的磁感应强度为 B e r I 2π 0 1 1 = 与线圈电流I2 交链的磁通链21 为 = 2 21 1 d S B S 若线框电流如图所示的顺时针方向,则dS 与B1方向 相同。那么 + + = = D b D D I a D b r r 0 I 1 a 0 1 2 1 ln 2π d 1 2π
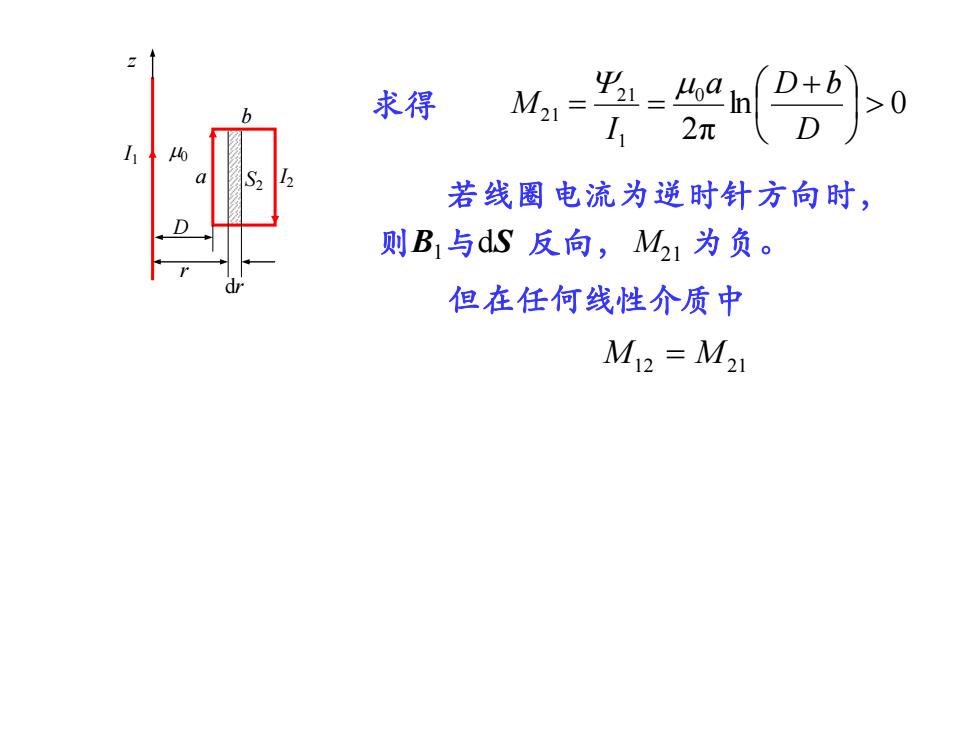
Y21D+boaM21求得CIr12元DI若线圈电流为逆时针方向时,则Bi与ds反向,M为负。但在任何线性介质中Mi2 = M21
求得 ln 0 2π 0 1 21 21 + = = D a D b I M 若线圈电流为逆时针方向时, 则B1与dS 反向, M21 为负。 a b dr r D I 0 1 I2 z S2 但在任何线性介质中 M12 = M21
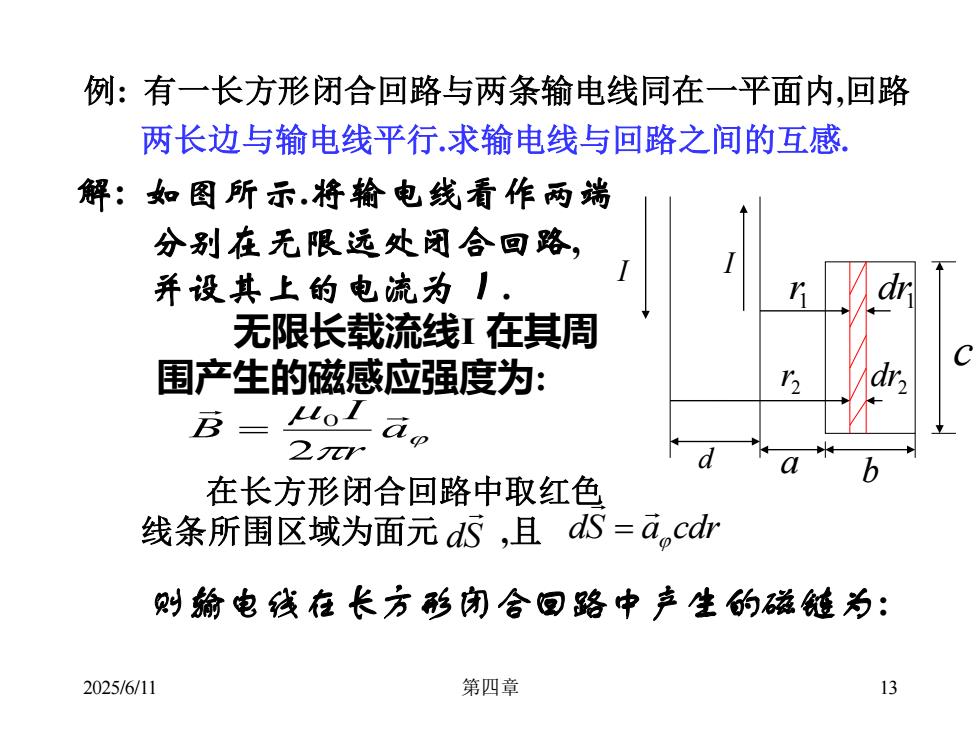
例:有一长方形闭合回路与两条输电线同在一平面内,回路两长边与输电线平行.求输电线与回路之间的互感解:如图所示.将输电线看作两端分别在无限远处闭合回路并设其上的电流为1.drr无限长载流线I在其周福dr围产生的磁感应强度为:r2B=uoTa2元aab在长方形闭合回路中取红色线条所围区域为面元 ds ,且dS=a,cdr则输电线在长方形闭合回路中产生的磁链为:13 2025/6/11第四章
2025/6/11 第四章 13 例: 有一长方形闭合回路与两条输电线同在一平面内,回路 两长边与输电线平行.求输电线与回路之间的互感. c I I d a b 1 r dr1 2 r 2 dr 解: 如图所示.将输电线看作两端 分别在无限远处闭合回路, 并设其上的电流为 I. 无限长载流线I 在其周 围产生的磁感应强度为: a r I B 2 = 0 在长方形闭合回路中取红色 线条所围区域为面元 dS ,且 dS a cdr = 则输电线在长方形闭合回路中产生的磁链为:

T2元r2元a+b+dMolca+bMolcrdr.r2元2元a+daLolc(a+b)(a+d)dab2元a(a+b+d)(a+b)(a+d)ΦLoc故互感为: M Y12元a(a+b+d)M/2 = M2大。只要求一个就行了。第四章142025/6/11
2025/6/11 第四章 14 I I d a b 1 r dr1 2 r 2 dr 2 2 0 1 1 0 2 2 cdr r I cdr r I a b d a d a b a + + + + = − a d Ic a b d a Ic a b + + + − + = ln 2 ln 2 0 0 ( ) ( )( ) ln 2 0 a a b d Ic a b a d + + + + = 故互感为: I M = ( ) ( )( ) ln 2 0 a a b d c a b a d + + + + = M21 M12 = 只要求一个就行了

二、内自感与外自感;1、外自感L。:如图穿过△S,的磁通为:Bdm2 = B, ·dS = B, ·ldrASdΦ=dΦ且dpm2与全部电流I交链。则mddΦe(4-8-4)11第四章152025/6/11
2025/6/11 第四章 15 二、内自感与外自感: 穿过 S2 的磁通为: d B dS B ldr m = = 2 2 2 且 dm2 与全部电流I 交链。则 d2 = dm2 I I d L e e = = 2 (4-8-4) 1 、外自感 Le :如图