
第一章力、热学实验买验一用三线摆测刚体的转动惯量转动惯量(momentinertia)是表征刚体转动特性的物理量,它描述刚体转动惯性的大小。例如,石油勘探开发中,涉及转动的机械部件非常多,如飞轮、发动机叶片、电动机转子等,在设计制造中往往需要考虑机械部件的转动性能,所以,研究物体的转动惯量很有实际意义。转动惯量的大小除与物体质量有关外,还与转轴的位置和质量分布(即形状、大小和密度)有关。如果刚体形状简单,且质量分布均匀,可以直接计算出它绕特定轴的转动惯量。但是工程实践中,我们常常碰到大量的形状复杂,且质量分布不均匀的刚体,理论计算极其复杂,通常采用实验方法来测定。转动惯量的测量,一般都是使刚体以一定的形式运动。通过表征这种运动特征的物理量与转动惯量之间的关系,进行转换测量。测量刚体转动惯量的方法有多种,三线摆法(three-wirependulum)具有设备简单、直观、操作方便、精度较高的优点。【实验目的】1.了解三线摆原理,并会用它测定圆盘、圆环绕对称轴的转动惯量。2.掌握测长度和周期的方法。3.加深对转动惯量概念的理解。【实验仪器】三线摆,待测样品(圆环一个),米尺,FD-MS-II计数计时仪【实验原理】如图1-1-1所示,支架1上面安装着可以转动的上盘4,在上盘上有3个铰
第一章 力、热学实验 实验一 用三线摆测刚体的转动惯量 转动惯量(moment inertia)是表征刚体转动特性的物理量,它描述刚体转动惯 性的大小。例如,石油勘探开发中,涉及转动的机械部件非常多,如飞轮、发动 机叶片、电动机转子等,在设计制造中往往需要考虑机械部件的转动性能,所以, 研究物体的转动惯量很有实际意义。转动惯量的大小除与物体质量有关外,还与 转轴的位置和质量分布(即形状、大小和密度)有关。如果刚体形状简单,且质 量分布均匀,可以直接计算出它绕特定轴的转动惯量。但是工程实践中,我们常 常碰到大量的形状复杂,且质量分布不均匀的刚体,理论计算极其复杂,通常采 用实验方法来测定。 转动惯量的测量,一般都是使刚体以一定的形式运动。通过表征这种运动特 征的物理量与转动惯量之间的关系,进行转换测量。测量刚体转动惯量的方法有 多种,三线摆法(three-wire pendulum)具有设备简单、直观、操作方便、精度较高 的优点。 【实验目的】 1.了解三线摆原理,并会用它测定圆盘、圆环绕对称轴的转动惯量。 2.掌握测长度和周期的方法。 3.加深对转动惯量概念的理解。 【实验仪器】 三线摆,待测样品(圆环一个),米尺,FD-MS-II 计数计时仪 【实验原理】 如图 1-1-1 所示,支架 1 上面安装着可以转动的上盘 4,在上盘上有 3 个铰
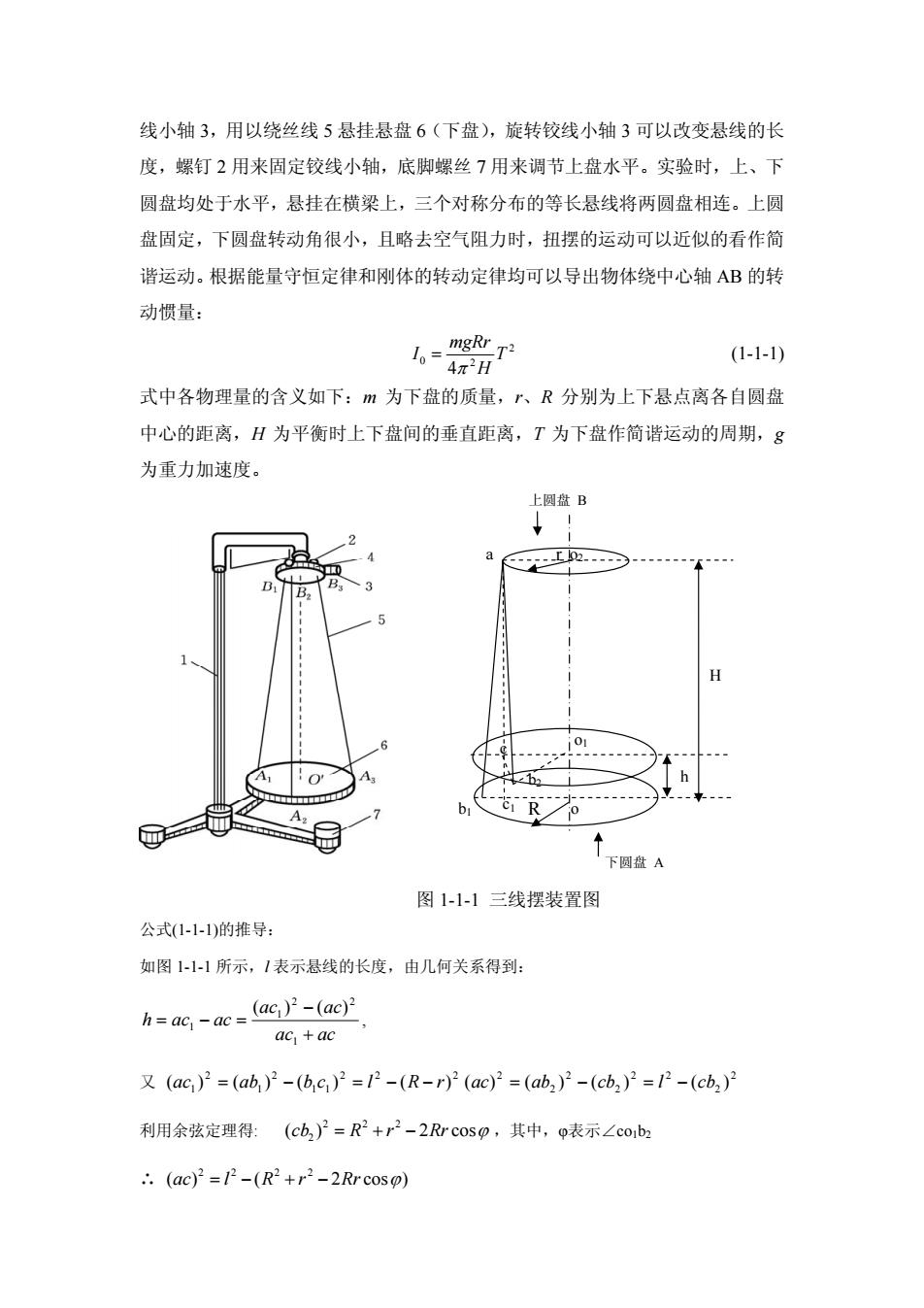
线小轴3,用以绕丝线5悬挂悬盘6(下盘),旋转铰线小轴3可以改变悬线的长度,螺钉2用来固定铰线小轴,底脚螺丝7用来调节上盘水平。实验时,上、下圆盘均处于水平,悬挂在横梁上,三个对称分布的等长悬线将两圆盘相连。上圆盘固定,下圆盘转动角很小,且略去空气阻力时,扭摆的运动可以近似的看作简谐运动。根据能量守恒定律和刚体的转动定律均可以导出物体绕中心轴AB的转动惯量:mgR_T?1。 =(1-1-1)4元2H式中各物理量的含义如下:m为下盘的质量,r、R分别为上下悬点离各自圆盘中心的距离,H为平衡时上下盘间的垂直距离,T为下盘作简谐运动的周期,g为重力加速度。上圆盘B+L102HU下圆盘A图1-1-1三线摆装置图公式(1-1-1)的推导:如图1-1-1所示,1表示悬线的长度,由几何关系得到:(ac,)2-(ac)h=ac,-ac=ac,+ac又 (ac,) =(ab,)2 -(b,c,) = [ -(R-r) (ac) =(ab,) -(cb,) = 12 -(cb,)2利用余弦定理得:(cb,)=R2+r2=2Rrcos,其中,Φ表示Zcoib2:: (ac) =1?-(R* +r?-2Rrcosp)
线小轴 3,用以绕丝线 5 悬挂悬盘 6(下盘),旋转铰线小轴 3 可以改变悬线的长 度,螺钉 2 用来固定铰线小轴,底脚螺丝 7 用来调节上盘水平。实验时,上、下 圆盘均处于水平,悬挂在横梁上,三个对称分布的等长悬线将两圆盘相连。上圆 盘固定,下圆盘转动角很小,且略去空气阻力时,扭摆的运动可以近似的看作简 谐运动。根据能量守恒定律和刚体的转动定律均可以导出物体绕中心轴 AB 的转 动惯量: 2 0 2 4 T H mgRr I π = (1-1-1) 式中各物理量的含义如下:m 为下盘的质量,r、R 分别为上下悬点离各自圆盘 中心的距离,H 为平衡时上下盘间的垂直距离,T 为下盘作简谐运动的周期,g 为重力加速度。 b h 2 o o1 c1 r R H 下圆盘 A c 上圆盘 B b1 a o2 图 1-1-1 三线摆装置图 公式(1-1-1)的推导: 如图 1-1-1 所示,l 表示悬线的长度,由几何关系得到: acac acac acach + − =−= 1 2 2 1 1 )()( , 又 22 2 11 2 1 2 1 −−=−= rRlcbabac )()()()( 2 2 22 2 2 2 2 −=−= cblcbabac )()()()( 利用余弦定理得: ( ) cos2 ϕ ,其中,φ表示∠co 222 2 −+= RrrRcb 1b2 ∴ )cos2()( 2222 −+−= RrrRlac ϕ

2Rr.2sin?2Rr(1-cosp): h=3ac,+acac+ac因为悬线长度l很长,B盘的偏转角の很小,故上式中的ac,~ac~H,那么2Rrsin?Rrp?2pph=又:sin”h=.2H2"22H上式两边同时对t求倒数,有:dh_pRrdpdtHdt不计摩擦力,系统机械能守恒,即1-1.0?+=mv?=constmgh+22dhdp而0=dtdt1dh/2dp21mgh+-lG2+=m()=const2dt2dt又圆盘的转动能量远比其上下运动的平动能大,所以将平动能略去后上式变为:1deymgh+=const)上式两边对t求导,得d'pmgRrdt?HIomgRr2元因为简谐振动的周期T=那么有,B圆盘简谐振动的角频率のHI.0mgRr?由以上两个式子可以求出Io=4元H将质量为m的待测圆环放在下盘上,并使待测圆环的转轴与AB轴重合。测出此时摆运动的周期T和上下圆盘间的垂直距离H。那么,可以求得待测圆环和下圆盘对中心转轴AB的总转动惯量为:I, -(m+m)gRr ?(1-1-2)4元H,如果不计因重量变化而引起的悬线伸长,则有H,=H。那么,待测物体绕中心轴AB的转动惯量为:
∴ acac Rr acac Rr h + ⋅ = + − = 1 2 1 2 sin22 )cos1(2 ϕ ϕ 因为悬线长度l 很长,B 盘的偏转角 φ 很小,故上式中的 ≈ ≈ Hacac1 ,那么 H Rr h 2 sin2 2 ϕ = 又∵ 22 sin ϕ ϕ ≈ , ∴ H Rr h 2 2 ϕ = 上式两边同时对 t 求倒数,有: Hdt Rrd dt dh ϕ ϕ = 不计摩擦力,系统机械能守恒,即 =++ constmvImgh 2 2 0 2 1 2 1 ω 而 dt dh v dt d , == ϕ ω ∴ const dt dh m dt d + Imgh + = 2 2 0 )( 2 1 )( 2 1 ϕ 又圆盘的转动能量远比其上下运动的平动能大,所以将平动能略去后上式变为: const dt d + Imgh =2 0 )( 2 1 ϕ 上式两边对 t 求导,得 ϕ ϕ )( 0 2 2 HI mgRr dt d −= 那么有,B 圆盘简谐振动的角频率 HI0 mgRr ω = ,因为简谐振动的周期 ω 2π T = , 由以上两个式子可以求出 2 0 2 4 T H mgRr I π = 将质量为m1的待测圆环放在下盘上,并使待测圆环的转轴与AB轴重合。测 出此时摆运动的周期 和上下圆盘间的垂直距离 T1 H1。那么,可以求得待测圆环和 下圆盘对中心转轴AB的总转动惯量为: 2 1 1 2 1 1 4 )( T H gRrmm I π + = (1-1-2) 如果不计因重量变化而引起的悬线伸长,则有 1 = HH 。那么,待测物体绕 中心轴 AB 的转动惯量为:

1=1,-1=_gRr[(m+m,)T2-mT2](1-1-3)4元H因此,通过长度、质量和时间的测量,便可以求出刚体绕某轴的转动惯量。由理论上推得的圆环绕中心轴的转动惯量为I理=I=!=m(R+R)(1-1-4)2其中,R,,R,分别为圆环的内外半径。比较I,I的大小。【实验内容】1.调节底座水平:将水平仪置于底座任意两旋钮之间,调整底座上的三个旋钮,使水平仪的气泡在中间。再把水平仪放到另外两旋钮之间,调整底座上的三个旋钮,使水平仪的气泡在中间,这时底座水平。2.调整下盘水平:将水平仪置于下盘任意两悬线之间,调整上盘上的三个旋钮,使水平仪的气泡在中间。再把水平仪放到另外两悬线之间,调整上盘上的三个旋钮,使水平仪的气泡在中间,这时下盘水平。3.测定悬线长1和上下圆盘中心到悬点的距离a和b,重复六次,并测量圆环和下盘的质量m、m1,以及圆环内外半径R,R。通过测出的两圆盘的相邻两个悬点间的距离a和b由等边三角形关系可算出R和r,即bR=a(1-1-5)mgab则(1-1-6)T1 = 4/3元 J3r -(a-b)gab4/3元/ /3P-(a-byg[(m+ m)7 -mT"1 (1-1-7)I环=I=l,-Io=4.测量空盘绕中心轴AB转动的运动周期T:轻轻转动上盘(上盘上有小转动杆),带动下盘转动,这样可以避免三线摆做扭动时发生晃动。注意扭摆的转角控制在5°以内。用FD-MS-II计数计时仪测定扭摆运动的周期T。5.测量待测圆环与下盘共同转动的周期T:将待测圆环置于下圆盘上,注意使两者中心重合,按上面的方法测出它们一起做扭摆运动的周期T
])[( 4 2 2 01 2 11 mTTmm H gRr III =−= −+ π (1-1-3) 因此,通过长度、质量和时间的测量,便可以求出刚体绕某轴的转动惯量。 由理论上推得的圆环绕中心轴的转动惯量为 )( 2 1 2 2 2 理 = ′ 1 += RRmII (1-1-4) 其中, 分别为圆环的内外半径。比较 21 ,RR , II ′ 的大小。 【实验内容】 1.调节底座水平:将水平仪置于底座任意两旋钮之间,调整底座上的三个旋 钮,使水平仪的气泡在中间。再把水平仪放到另外两旋钮之间,调整底座上的三 个旋钮,使水平仪的气泡在中间,这时底座水平。 2.调整下盘水平:将水平仪置于下盘任意两悬线之间,调整上盘上的三个旋 钮,使水平仪的气泡在中间。再把水平仪放到另外两悬线之间,调整上盘上的三 个旋钮,使水平仪的气泡在中间,这时下盘水平。 3.测定悬线长 和上下圆盘中心到悬点的距离a和b,重复六次,并测量圆环 和下盘的质量m、m l 1,以及圆环内外半径 。通过测出的两圆盘的相邻两个 悬点间的距离a和b由等边三角形关系可算出R和r,即 21 ,RR 3 , 3 b r a R = = (1-1-5) 则 2 22 2 0 )(334 T bal mgab I −− = π (1-1-6) ])[( )(334 2 2 11 22 2 01 mTTmm bal gab IIII −+ −− =−== π 环 (1-1-7) 4.测量空盘绕中心轴 AB 转动的运动周期T :轻轻转动上盘(上盘上有小转 动杆),带动下盘转动,这样可以避免三线摆做扭动时发生晃动。注意扭摆的转 角控制在 5°以内。用 FD-MS-II 计数计时仪测定扭摆运动的周期 T。 5.测量待测圆环与下盘共同转动的周期 :将待测圆环置于下圆盘上,注意 使两者中心重合,按上面的方法测出它们一起做扭摆运动的周期 。 T1 T1
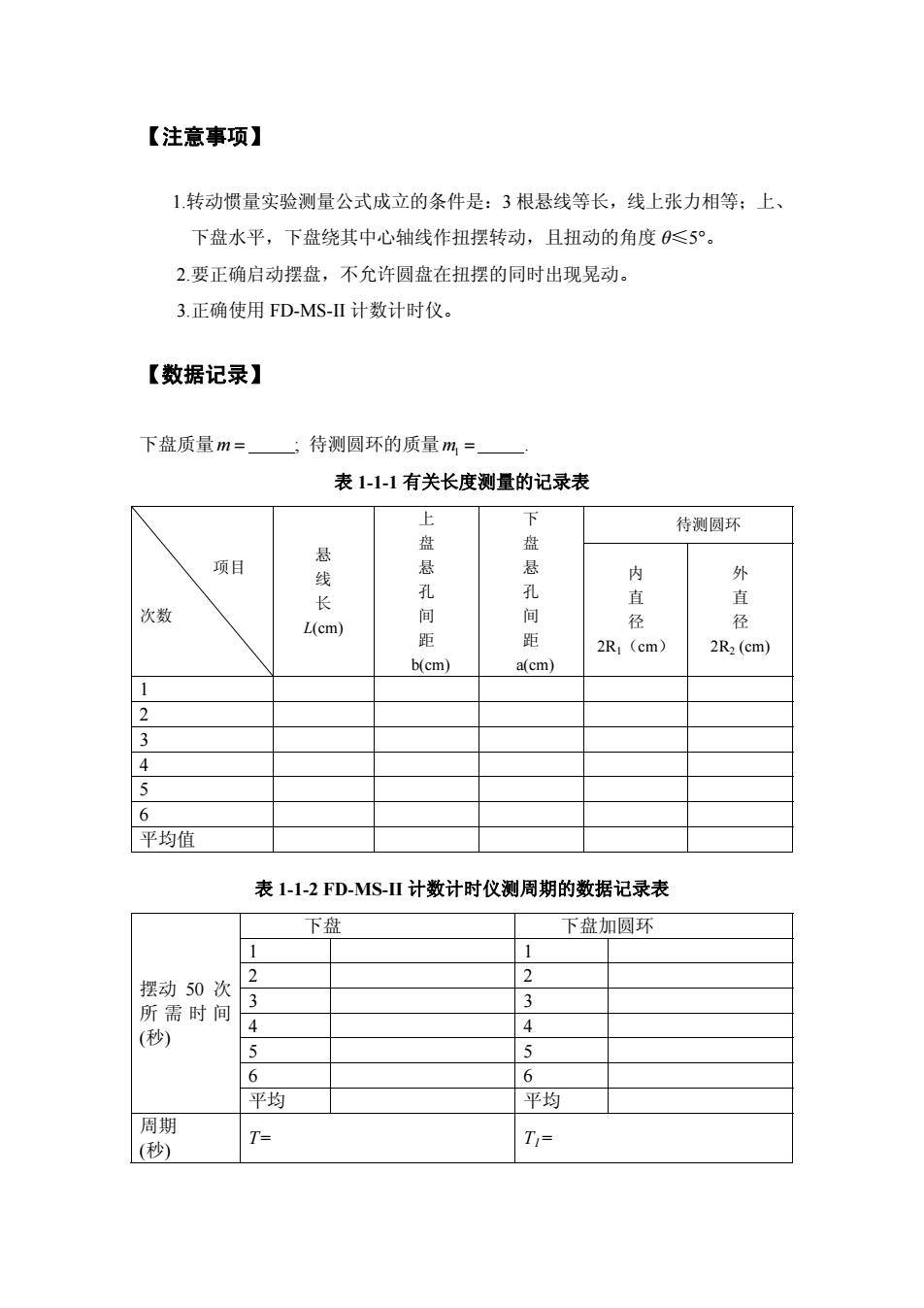
【注意事项】1转动惯量实验测量公式成立的条件是:3根暴线等长,线上张力相等:上下盘水平,下盘绕其中心轴线作扭摆转动,且扭动的角度≤5°。2.要正确启动摆盘,不允许圆盘在扭摆的同时出现晃动。3.正确使用FD-MS-II计数计时仪数据记录)下盘质量m=:待测圆环的质量m=表1-1-1有关长度测量的记录表上下待测圆环盘盘悬悬悬项目内外线孔孔直直长次数间间径径L(cm)距距2R(cm)2R2 (cm)b(cm)a(cm)123456平均值表1-1-2FD-MS-II计数计时仪测周期的数据记录表下盘下盘加圆环1122摆动50次33所需时间44(秒)5566平均平均周期T=T,=(秒)
【注意事项】 1.转动惯量实验测量公式成立的条件是:3 根悬线等长,线上张力相等;上、 下盘水平,下盘绕其中心轴线作扭摆转动,且扭动的角度 θ≤5°。 2.要正确启动摆盘,不允许圆盘在扭摆的同时出现晃动。 3.正确使用 FD-MS-II 计数计时仪。 【数据记录】 下盘质量m = ; 待测圆环的质量m1 = . 表 1-1-1 有关长度测量的记录表 待测圆环 项目 次数 悬 线 长 L(cm) 上 盘 悬 孔 间 距 b(cm) 下 盘 悬 孔 间 距 a(cm) 内 直 径 2R1(cm) 外 直 径 2R2 (cm) 1 2 3 4 5 6 平均值 表 1-1-2 FD-MS-II 计数计时仪测周期的数据记录表 下盘 下盘加圆环 1 1 2 2 3 3 4 4 5 5 6 6 摆动 50 次 所需时间 (秒) 平均 平均 周期 (秒) T= T1=