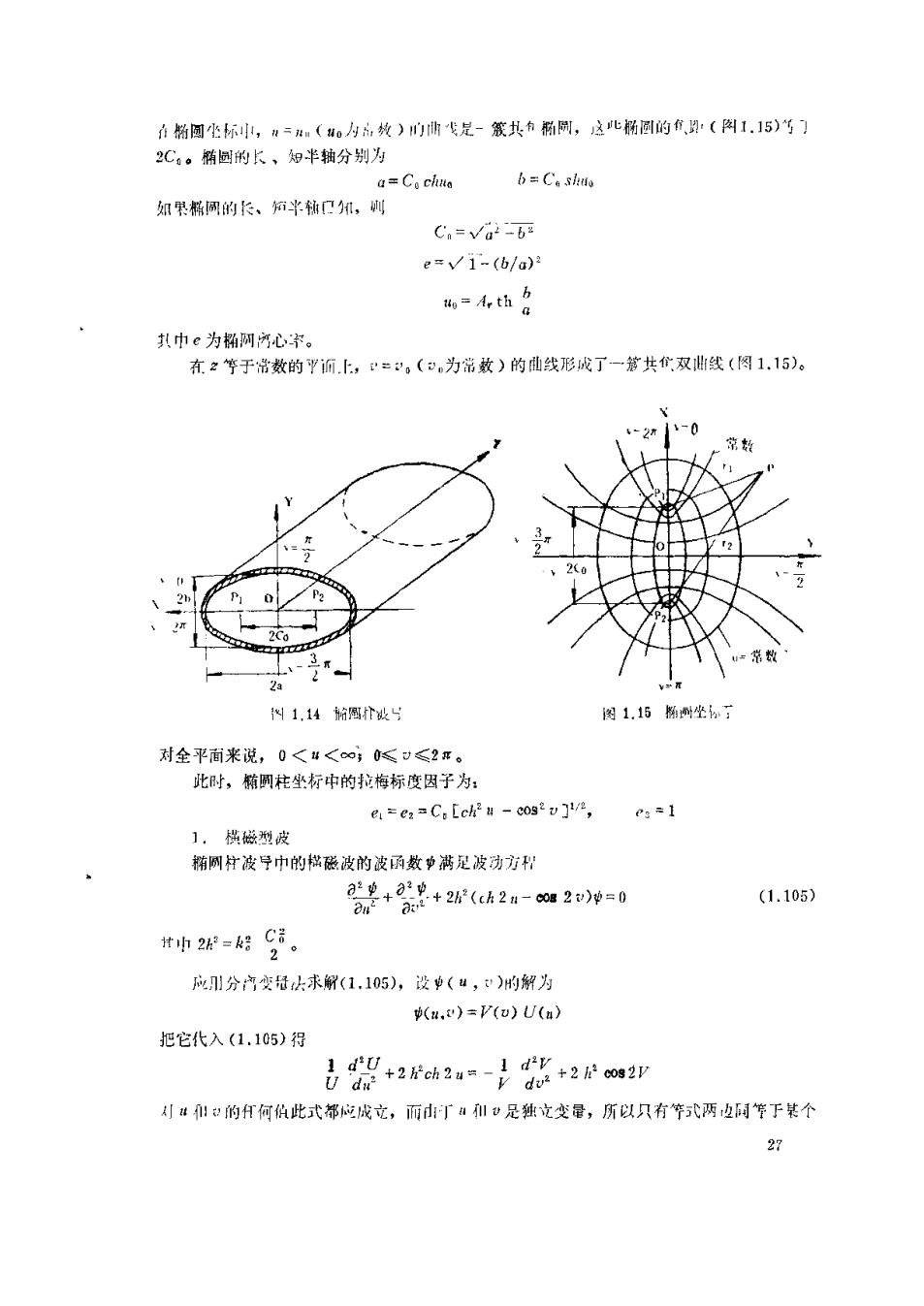
在粉圆坐标,n=m(o内,效)门曲生是-簇共有椭刷,这北肠圆的有,理:(网1.15)等 2C0。椭圆的长、知半轴分别为 a=C。chra b=Ca shto 如果椭闹的长、佰半和口和,叫 Cn=√a2-bz e=√1-(b/a)2 4o=Arth b 其巾e为搦网河心茶。 有2等于常数的而上,=。(为常数)的l线形成了一第共食双出线(图1.15)。 -0 常数 2(0 21 0 '2 2C 3.K 2a 物1,14网t设号 图1.15椭例坐了 对全平面来说,0<4<∞;≤≤2π。 此时,椭圆柱坐标中的拉梅标度因子为: e=e2=C.[ch?u cos2v], cg÷1 】,横磁型皮 椭圆柱波导巾的拙磁波的波函数中满足皮功方刊 a2+22+2(h2H-082up=0 (1.105) 2n2 #办2然=好。 1分产变tk求解(1.105),设(4,)的解为 (u,)=V(o)U(u)》 把它化入(1.105)得 己器+2oh2=-是+2r 的何何伯此式都应成立,而丁和是独立变量,所以只有等式两边同管于某个 27
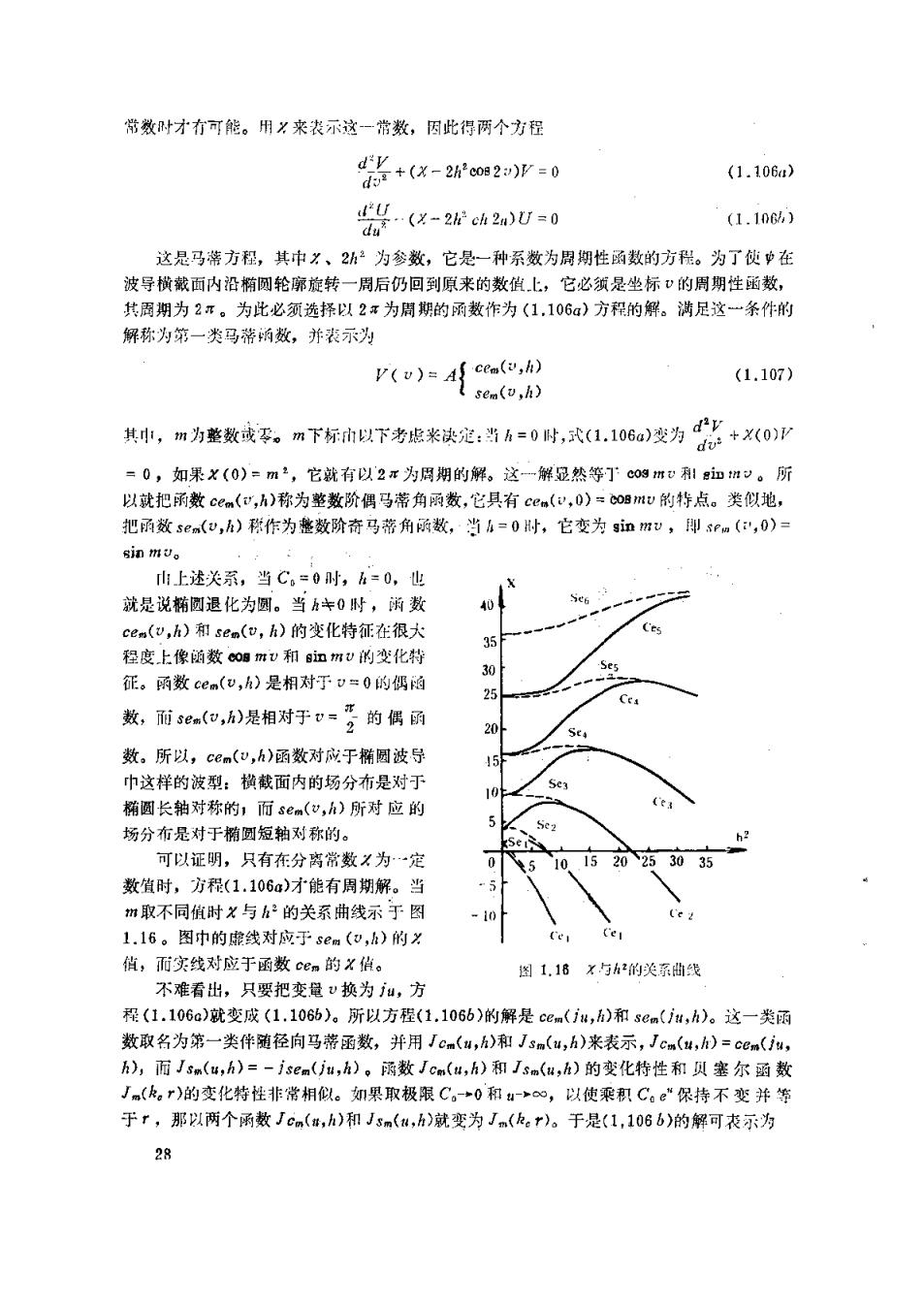
常效附才行可能。用?来表示这一常数,因此得两个方程 +(X-2h2coa2)p=0 d'v (1.106) du(x-2h ch 2n)U=0 U (1.106) 这是马蒂方程,其中?、2为参数,它是一种系数为周期性函数的方税。为了使中在 波导横戴面内沿椭圆轮廓旋转一周后仍回到原来的数值上,它必领是坐标·的周期性函数, 其周期为2π。为此必须选择以2x为周期的函数作为(1,106a)方释的解。满足这一条件的 解称为第一类马蒂函数,并表示为 V(v)=AS cem(v,h) (1.107) t sem(v,h) 其,m为整数或零。m下标以下考虑米决龙:当h=0时,式(1.106)变为+(0)p =0,如果X(0)=m2,它就有以2π为周期的解。这一解显然等门C9m心!加m。所 以就把函数cem(”,h)称为整数阶偶马蒂角函数,它具有cem(',0)=COBmU的特点。类似地, 把函数sem(,h)称作为整数阶奇马蒂角函数,当h=0时,它变为nmU,即sPm(',0)= sin mv。 山上述关系,当C。=时h=0,也 就是说椭圆退化为圆。当五丰0附,函数 40 56 cem(),h)和sen(v,h)的变化特征在很大 35 程度上像函数COB mU和inmV刊变化特 30 征。函数cem(v,h)是相对于=0的偶函 25 Cea 数,而se(包,A)是相对于v=号的偶函 20 数。所以,cem(v,h)函数对应于椭圆波导 5 巾这样的波型:横截面内的场分布是对于 Se3 10 椭圆长轴对称的,而sem(v,h)所对应的 场分布是对于椭圆短轴对称的。 5e2 h2 可以证明,只有在分离常数X为一定 5 5 20253035 数值时,方程(1.106a)才能有周期解。当 m取不同值时X与h2的关系曲线示于图 -10 1.16。图中的虚线对应于sem(w,h)的为 俏,而实线对应于函数cen的名伯。 图1.18X与h2的关系曲线 不难看出,只要把变量v换为j4,方 程(1.106a)就变成(1.106b)。所以方程(1.106b)的解是cem(iw,)和sem(jH,h)。这一类函 数取名为第一类伴随径向马蒂函数,并用Jcm(w,h)和Jsn(u,h)来表示,Jcm(,h)=cem(iu, h),而J3m(4,h)=-jsem(jw,h)。函数Jcm(u,h)和Jsm(u,h)的变化特性和贝塞尔函数 Jm(。r)的变化特性非常相似。知果取极限C。-→0和u-~∞,以使乘积Cae“保持不变并等 于r,那以两个函数Jcm(#,h)和Jsm(u,)就变为Jm(k。r)。于是(1,106b)的解可表示为 28

U(u)=uh) t Jsm(u,k) (1.108) 现在4的变化范围是从零到4。把1.107)与(1.108)相乘则得到(4,v)的解 Jcm(u,h)cem(v,h) (u,)=Amn,Asen(,h) (1.109) 把(1.109)代入(1.62)式就得到椭圆波导中TM被的场分量表达式 Jcm(u,h)cem(U,h) Yon Amn u √0h4-og0 Eu=干 Ymn 是Jsa(a,h)sem,h) d Jom(u,h)e E知*千an编 cem(v,h) chiu-00sv eFYm (Jsa(4,hù3品sem《u,h) a-红加的e Jon(u,h)2 joe Amin a元cem(巴,h) H.=千Vi-6o00 Jsn(,》品ente,h) joc。hn j品ea(wh)cea, H,=±7o-o可1sna,Aeno,) ei'mnt au IH,30 (1.110 利用边界条件来决Ek。,即在波导壁(·=∞时)上应有(o,)=0。由(1.109)得 Jcm(uo,h)=0 (1.111) Jsm(e,h)-0 (1.112) 无论是(1.111),还是(1.112)都有无限多个自变量值能使径向马蒂函数等于零。把这 些自变量值叫做第一类径向马蒂函数的根,并分别用九mn和hmn表示,其中?为根的序号。 每一个根刈应寸个。值,由下式确龙 为E。m波: ko:mn=2hcm/Co 对Emn波: koimn 2hamn/Co (1.113) 每一刈nn值刈应于一龙的皮导场结构。图1,17画出了E:,上1相E1反的场结 构。 出(1.113)可求出截止波长 对Emn皮: rwn=元CG/h6mn (1,114) 对Enn皮: C,ma=rC6/h附n 29

t E 内【17儿科北收的场结 。描电型波 横电型皮所、是水的皮心域中*的解也为 u-{的o的 (1.115) 把(1.115)代入(1.54),或在(1.110)式施行对偶变换,即以F,与H,(=#,心,z)对换,以 μ。代换。,使可立即得到横电波的场分量表示式。 .值仍由边界条件确。此时,要水沙》=0,行 On 2Jcm(4o)=0 a地*(o:0) an (1.116) an asa(oh)=0 力程(1.116)有九根多个根,我们川川:s利和好m来表示这些根。问花改的格况-!。 根:mm对烂」1I。皮,达种破型的场分显在皮子横截阳内的分相对于椭圆的长轴是称 的;mn为应上H放,这种皮是对椭圆的短轴刈称的。。位出下式确处 对Hcm库波: A。,nn=2h:ma/C0 (1.117) 11m及: k.,4=2m/(a 阳应时鼓止及长月 I1:wn支: 方mw=xC/h!nn (1,118) 灯H性以: i,an兰TCo/himn 30
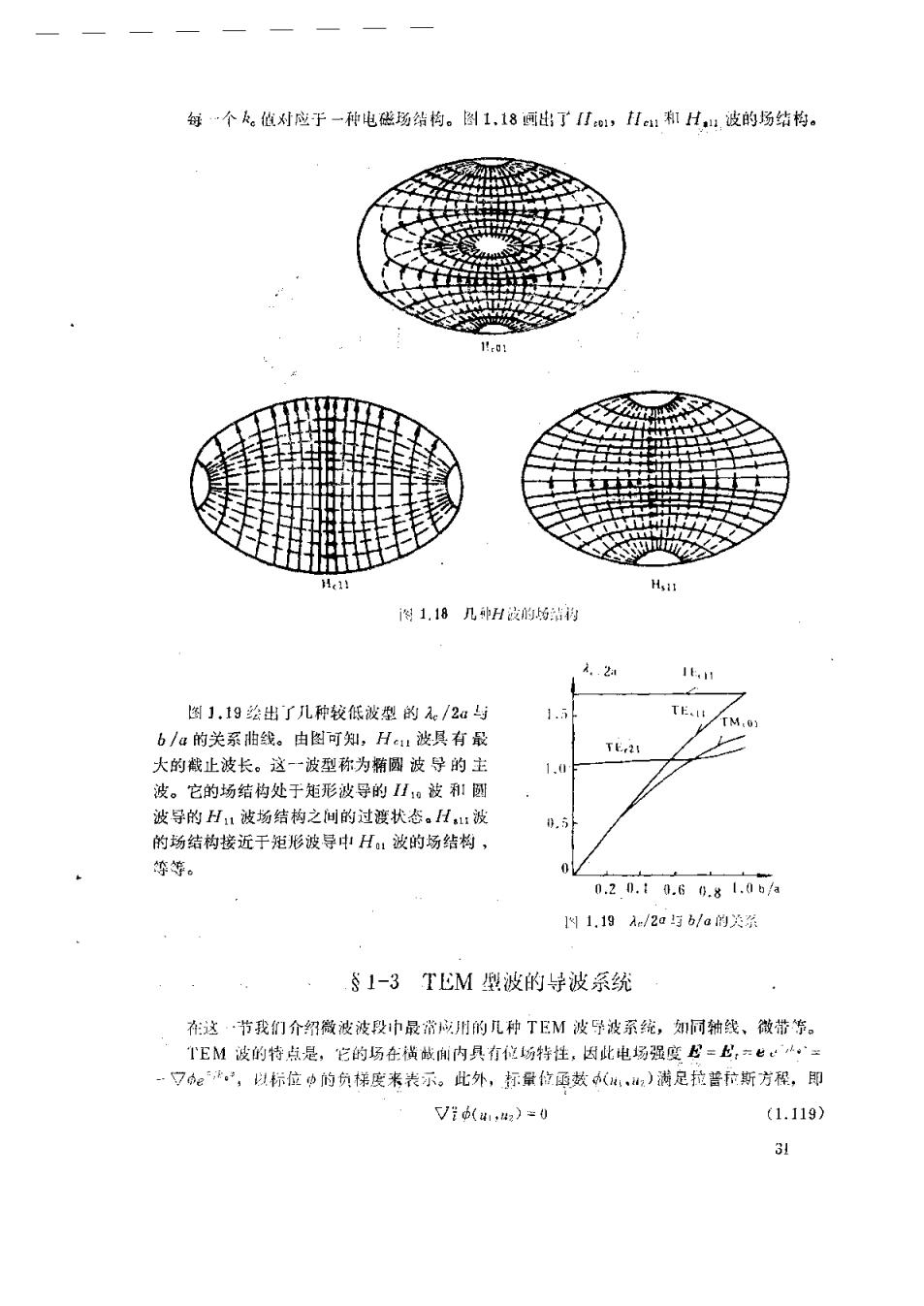
每…个。值对应于一种电磁场结构。图1,18画:了o,1c:和H,:波的场结构。 1.18几H波的均站为 1t,1 图1.19绘出了几种较低被型的e/2a与 1.n TE. TM.0) b/a的关系曲线。由图可知,Hu波具有最 TE 21 大的截止波长。这一波型称为椭圆波导的主 1.0 波。它的场结构处于矩形被导的【1。波和!圆 波导的H1波场结构之间的过渡状态。H1:波 0.5 的场结构接近于矩形波导中H:波的场结构, 等等。 0 0.2.0.t.60.81.0b/a 11.19Ar/2a与b/a的关系 §1-3TEM型波的导波系统 在这·节我们介绍微波波段市最常成用的几种TEM波导波系统,如同轴线、微带係。 TEM波的特点是,它的场在横战内具有位场特性,因比电场强度E=E,六七k。✉ 7。,以标位中的负梯度来表示。此外,标量位函鼓(,2)满足拉普拉斯方程,即 Vi(41,42)=0 (1.119) 31