
TM波的最低阶的传播波是:=n=1的波,其藏止汝长为2动/(a2+力)。与TE波 比较可以知道,矩形波子截上:波长 最大的传播波是TE,波型,因而它 TM:t 是主波。同时,还要指出具有同样指 年 数m,n的TEmn和TMm,波,由 于它们具有相同的传播常数,而成为 folfo 简并波。 假使要使波导巾只有一·种波刚传 EE9 摇,我们必须选取适当大小的a,b。 如米A是工作波长,欲使TE知型波 88e89g (a) 传播,则必氖满足下列关系式: 芒角所 A<hono:A>hen2o 除了考虑传输TF。单模之外,还要 ⊙可朗 考虑衰威等因素,一般取 a≈0.71a,b≈0.3510 29a2姐 式中入是电磁波弃自虫空闻中的波 联 长。 从上述讨论可见TM波和T卫波 6889 是对偶的,除了稍有差别之外,基本 上具有同样的性质。因此,我们花下 图1.10矩形波5导TM1和TM2议的场分布 面以TE1波为例,说明矩形波导中传播波型某本特性参数的计算。 3.炉形波牙:传播主波型的基术性质 山.上所述,可TF。波的波诵数嘉=4。ogπx。波导小电磁场分录直接由(1.81) 式得: H。=t4(日)。e… h,-()广五c9s*o E,a-ja4,()in… (1.86) Hg=,=E:0 其参数kc,0,Y1。和Za为: kevio (1.87a) =[(}-始] (1.87b) 7A=-E/H.=.jouo Y1n (1,87c) 22

因为域:波cw=2a.所以波子波长,为 1,=8。=[1-/2)7, Au (1.87d) 相速和群速分别为 =” 10 (1.87c) vo=Alve alodol ieee (1.87f) ,'alojotolo、 Ag 也磁场各个分量在波导面上的分 远五7苏立 布如图1.11所示。电磁场的相位仅是 772 2的函数,因此式(1.86)表示沿2轴 方向传播的平而波。但因F,是¥的 函数,这种平首波是不均匀的。 3 (u) 2 根据§1.2所述的普遍关系,我 1.11形波导中T严。波的场分而 们出(1.63)式把费代入,可水特TF1。波型传播功*的时间平均作 P=号2,点An(日)o=l4toz(.)月 (1.88) 波于中的丧减,当为空气填充时,依(1.7)式进行计算,而该式的分丹为2),分子是波导 壁上的损耗功,其为 P=号见fB品nx7:姊+:单门dl 上式的积分是沿着波导的横截而的边界1取的。在和y轴方向平的波导整上,每单位长度 所损耗的功帘为 a=心好。dy龙k好61a 在和轴方向平行的两波导壁上,每单位长度的波导所损耗的功率为 Pa=R.0B品nx又:+6好*d =R,j09股-()im+好eogn年]加d =号北,号铝aA户 波导每单位长度的总损耗为 P+m:=号北好候1+岛 所以 。=经熊1+品2是会+% (1.89) 上式中a、b、1都以米为单位,α的单位则为奈贝/米。从公武(1.89)看出,在空心矩形 波导中传播的主波型的哀减,不仅取决于波长1,而与波导尺寸a和b的值有关。比伯 b/4愈小,则波导的衰减愈大。但阳是,在实际中,为了防止高次波型在波导中传播,a值必 29

须大丁于/2,而值必须小于/2,/比俏约为1/2。从(1.8)式可求出α为最小时的頫 杂值。 四、圆形波导 图1,12表示半径为a的圆截而柱形波导。鉴丁它涉及到圆柱形,故州圆柱坐标来分析最 为合适。此时,u1=r,2=P,a=之,而标度因子 e1=1,g2=r,es=1。 由于圆波导的波型所具有的一般性质类似于知形波 导,所以在这里不作详细讨论。 1.横磁波型 对横磁波型来说,要求方程式 V程约+:约=0 2a 的解在r=a处为零。当我们把横向拉普拉斯算符 图1.12洞挂形波导 了:用圆柱坐标表示时,此方程变为 票+}9票+品8+好=0 (1.90) 用分离变量法可把上述方程式化为两个常微分方程。假定解是(”,P)=R(r)(9),把它代 入(1.90)式,并用R(r)p(9)除方程得 1d'R 市*,46 器+市达 r坊d0+=0 用r乘上式得 r*d'R r dR Rdrat Rdr +k好r2=-1d ddp 上式左边只是”的函数,而右边只与有关。无论r与P取任何数值都应该满足。由于”和 P是独立变量,所以只有当等式的左右等于同一个常数时才有可能。用m表示这个常数, 这样就得到两个方程式: 器+}器+(-)=0 (1.91a) r dr d d0+m2功=0 (1.91b) 在这种情况下,波导内的场随平的变化必须以2π为周期,才是单值的,为此必须使m 等整数或零。方程(1.91b)的解为 i=40ogm印 (1.92) 《8 in m (1.91a)式是贝塞尔微分方程,它的解为 R=BZm(k。r) (1.93) 其中Zm(k。r)是变量为k。r的m阶柱函数。现r的变化是由0到a(圆的半径)。当变量 为零时,第二类和第三类贝塞尔函数等于无穷大。因为功在任何地方都不可能等于无穷大, 显然在这种情况下必须把Zm(k。)取为无论变量为任何值时都是有限的第一类贝塞尔函数。 24

因此,得 (r)=BJm(k。r) 的er)(m)=.1n(k.r)o9x (1.9) tgin甲 Am=AB 把(r,p)与p的关系表示为co9n或snip是没有任何区别的。把c0smp换成sinm 等于把P的起始读数改为90°。用0mP来表示与P的关系,行到中的解为 (r,p)=Amn Jm(ke r)cosm (1.95) 为了确定电磁场的各分景,则只要把(1.95)式代入式(1.62)便可得到。 上述式的。要用边界条件来确定,花波导整(G=∞)的表面上华应等零。(1.95) 可得 Jm(kea)=0 (1.96) 有无限多个变量值可使贝塞尔函数等于零。这些变量伯称为贝塞尔函数的根,川P来 表示它,在表1,1中列出了m取不同数值时贝塞尔函数的前几个根。 每一个根对应于一个。伯,并拍等式 kemnan (1.97) 来确定。如同东:形波导中的帮况那样,侧波导也有无限多对解。 表1.1TM波的Pma值 2 3 5 Pmn 2.405 5.520 8.654 11.792 14.931 1 3.832 7.016 10.173 13.324 18.471 2 5.136 8.417 11.620 14.796 17.960 每一组m和n,都对应着一种特定的TMm波型。整数m表示场沿圆周的变化次数。 而”表示场沿径向的变化次数。mz波的传播常数为 -=号-(a门 (1.98) 截止:波长为 (1.99) 波阻抗为 2.=%2. (1.100) 利川一般关系式(1.64)和(1.75)可分别计算TM型波的能流与衰减。 2,横电型波 25
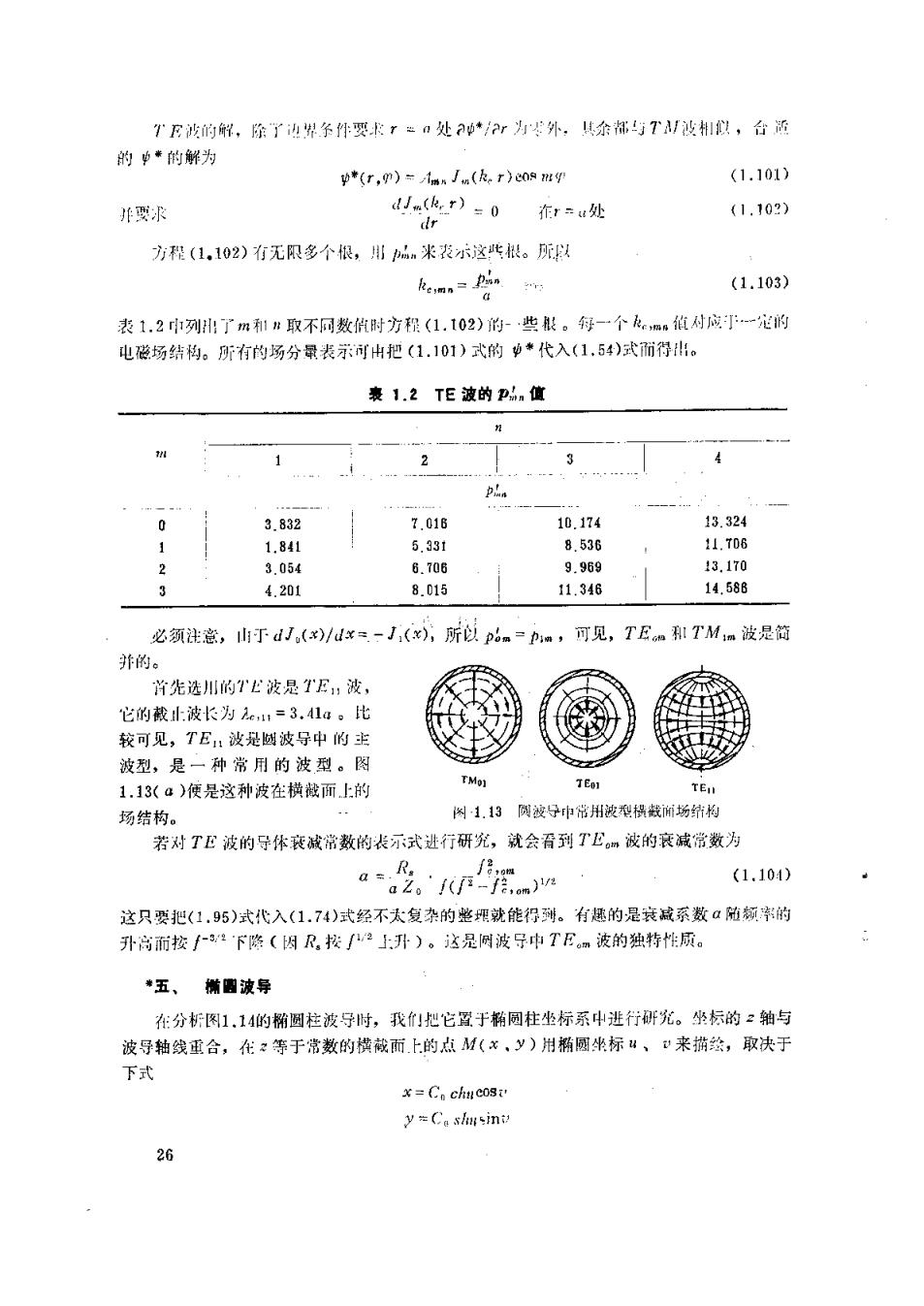
T究沙的解,除了边根尔件要求?出处P*r为外,其余都与T被相似,台活 的单*的解为 (r,m)=1mn I(ke r)eos m (1.101) 非要求 dJn(k.r)=0 在r=处 (1.102) dr 方程(1,102)有无限多个根,用n米表这些根。所以 kmn二n (1.103) 表1.2中列了m和n取不同数时方程(1.102)-·些服。每-一个mn值对应龙的 电德场结构。所有的场分量表示可中把(1.101)式的*代入(1,54)式而得出。 表1.2TE波的pn值 2 pin 4+4=4444 0 3.832 7.016 10.174 13.324 1 1.841 5,331 8.536 11.T06 2 3.054 6.706 9.969 13.170 3 4.201 8.015 11.346 14.58B 必须注意,l于dJ,(x)/x=-Ji(x),所以p6m一pm,可见,TEon ITMim波是简 并的。 首先选川的T北波是TE,波, 它的截止:波长为e,=3.41a。比 较可见,TE:波是憾波导中的主 波型,是一种常用的波型。图 1.13(a)便是这种波在横谳而上的 TEol TE 场结构。 肉1.13例被导中常用波型祸载场缔构 若对TE波的导体衰减常数的表示式进行研究,就会看到TEm波的衰减常数为 am (1.104) 这只要把(1.95)式代入(1.74)式经不太复杂的艷理就能得列。有趣的是衰减系数a随频的 升高而按f3:2下路(因,按2上升)。这是网波子中TE。m波的独特性质。 *五、椭图波导 在分析图1.14的椭圆柱波导时,我把它置于椭圆柱坐标系中进行研究。坐标的2轴与 波导轴线重合,在?等于常数的横薇而上的点M(x、y)用椭圆坐标4、来描绘,取决于 下式 x=Cn chuc08i y =Ca shusinu 26