
http://lxy.xidian.edu.cn/shumo/ 基本求解方法)一分支限界算法 基本思路:先去掉整数约束求解相应的线性规划,若解x 为整数则结束,否则该线性规划的最优值cTx是P问题的上 界U,而P的任一可行解对应一个下界L;进一步将可行域 分枝,逐步减少上界和增大下界,二者相等时终止算法。 min c"x min c"x min c"x s.t.Ax=b s.t.Ax=b s.t.Ax=b →→ x≥0 x≥0 x≥0 x,≥Lx+1 x,sx」 x∈Zm x∈Z axz=40x,+90x2 上界U=356,→(4.81,1.52) S.t.9x1+7x2≤56 下界L=0,→0,0) 7x1+20x2≤70 将原问题分成2个子问题: x1≥0,x2≥0 1)原规划加上≤4; 2)原规划加上x≥5; 1,X2为整数
http://lxy.xidian.edu.cn/shumo/ 基本思路:先去掉整数约束求解相应的线性规划,若解x 0 为整数则结束,否则该线性规划的最优值c Tx 0是IP问题的上 界U,而IP的任一可行解对应一个下界L;进一步将可行域 分枝,逐步减少上界和增大下界,二者相等时终止算法。 max 40x1 90x2 z = + 0, 0 7 20 70 . . 9 7 56 1 2 1 2 1 2 + + x x x x s t x x x1 , x2为整数. 上界U=356,→(4.81,1.52) 下界L=0,→(0,0) 将原问题分成2个子问题: 1)原规划加上x1≤4; 2)原规划加上x1≥5; 基本求解方法1)——分支限界算法 + = n i i T x Z x x x s t Ax b c x 1 0 . . min 0 = x Z x x x s t Ax b c x i i T 0 0 . . min n T x Z x s t Ax b c x = 0 . . min
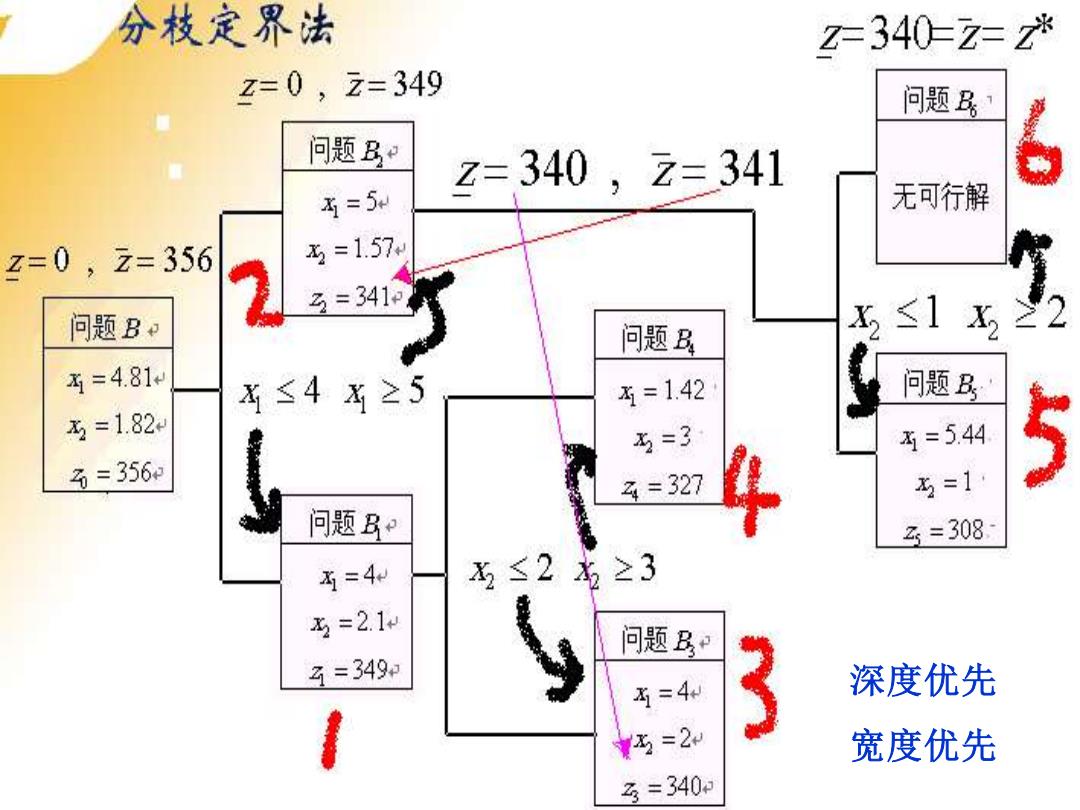
分枝定界法 Z=340-z=z* z=0,z=349 问题B 问题B z=340,z=341 五=5 无可行解 z=0,z=356 五=1.57w 2 3=341P 问题Be 问题B ≤12 5=4.81 ≤4x≥5 五=1.42 问题B x=1.82 五=3 =5.44 石=356 4=327 五=1 问题Be 35=308 五=4 为≤2本≥3 五=2.1 问题B 3=349知 西=4 深度优先 五=2 宽度优先 3=340
http://lxy.xidian.edu.cn/shumo/ 深度优先 宽度优先